THE SOUND OF FRACTIONS
teaching inherently abstract representations from an aural and embodied approach
Christopher Special Frisina
Thesis submitted to the faculty of the Virginia Polytechnic Institute and State University in
partial fulfillment of the requirements for the degree of
Master of Science
In
Computer Science
Dr. Deborah Tatar - Advisor
Dr. Kurt Luther – Committee Member
Steve Harrison – Committee Member
Tuesday, May 3, 2016 @ 9:30 am
Blacksburg, Virginia and online specialorange.org/thesis
Keywords:
Music Performance; Fraction Learning; Mathematics; Drumming; Coordination; Entrainment;
Multi Representations


The Sound of Fractions
5
1 LIST OF TABLES ............................................................................................................................... 9
2 LIST OF FIGURES ........................................................................................................................... 10
3 ABSTRACT ..................................................................................................................................... 12
4 INTRODUCTION ............................................................................................................................ 13
5 LITERATURE REVIEW .................................................................................................................... 14
5.1 COMMON THEMES IN MATHEMATICAL INSTRUCTION .............................................................................. 14
5.2 COMMON THEMES IN MUSICAL INSTRUCTION ........................................................................................ 17
5.3 MATH, MUSIC, AND IN BETWEEN ........................................................................................................ 18
5.3.1 Revisiting Educational Approach to Mathematics ............................................................. 18
5.3.1.1 Rational Number Project (RNP) ............................................................................................................18
5.3.1.2 The Splitting Loope ..............................................................................................................................18
5.3.1.3 Equal Sharing .......................................................................................................................................20
5.3.2 Musical Theory as an Analogy to Mathematical Theory .................................................... 20
5.3.2.1 Useful Components of Musical Theory .................................................................................................21
5.3.2.2 Entrainment ........................................................................................................................................22
5.3.2.3 Embodied Interactions .........................................................................................................................23
5.3.2.4 Expectation..........................................................................................................................................23
5.3.3 Elements of Educational Approach .................................................................................... 24
5.3.3.1 Scaffolding ...........................................................................................................................................24
5.3.3.2 Engagement ........................................................................................................................................24
5.3.3.3 Proximity .............................................................................................................................................24
5.3.3.4 Synchronous Coordination ...................................................................................................................25
5.3.3.5 Communication ...................................................................................................................................25
5.3.3.6 Micro-coordination ..............................................................................................................................26
5.3.4 Building Better Representational References ..................................................................... 26
5.3.4.1 Culture & Ethnomathematics ...............................................................................................................27
5.3.4.2 Cross-domain teaching .........................................................................................................................27
5.3.5 The Role of Technology in Mathematics Learning.............................................................. 27
5.4 OTHER CROSS-DOMAIN APPROACHES .................................................................................................. 28
5.4.1 Music................................................................................................................................ 28
5.4.2 Food ................................................................................................................................. 28
5.4.3 Dance ............................................................................................................................... 28
5.4.4 Embodied ......................................................................................................................... 28
6 OUR PRIOR WORK ........................................................................................................................ 28
6.1 PROTO COMPUTATIONAL THINKING ..................................................................................................... 29
6.1.1 Proof of Concept ............................................................................................................... 29
6.2 REDESIGN AND CONJECTURES ............................................................................................................. 30
6.2.1 Agency ............................................................................................................................. 30
6.2.2 Design .............................................................................................................................. 30
6.2.2.1 For The Individual ................................................................................................................................30
6.2.2.2 With The Group ...................................................................................................................................31
6.2.3 Brainstorming Sessions ..................................................................................................... 31
6.2.3.1 Representations ...................................................................................................................................31
6.2.3.2 Layout .................................................................................................................................................33
6.2.4 User Interface (UI) Components ........................................................................................ 34
6.2.4.1 Instruments .........................................................................................................................................34
6.2.4.2 Labels ..................................................................................................................................................34
6.2.4.3 Transitions ...........................................................................................................................................35
6.2.4.4 Technology ..........................................................................................................................................35
6.3 ITERATIVE REDESIGNS ....................................................................................................................... 35
The Sound of Fractions
6
6.4 MOVING TOWARDS FUTURE OPPORTUNITIES .......................................................................................... 36
7 THE MAIN STUDY.......................................................................................................................... 37
7.1 MOTIVATION AND GOALS .................................................................................................................. 37
7.2 CURRICULUM .................................................................................................................................. 37
7.3 PROGRAMMING AND UI .................................................................................................................... 38
7.4 PROSPECTIVE STUDENTS .................................................................................................................... 38
8 CURRICULUM ............................................................................................................................... 38
8.1 EDUCATION REQUIREMENTS............................................................................................................... 38
8.1.1 Virginia (VA) Standards of Learning (SOLs) ........................................................................ 39
8.1.2 Common Core ................................................................................................................... 41
8.2 GOALS AND TASKS ........................................................................................................................... 43
8.3 STAGES .......................................................................................................................................... 44
8.3.1 Stage 1 : Creation ............................................................................................................. 44
8.3.1.1 Curriculum & Tasks ..............................................................................................................................45
8.3.2 Stage 2 : Identification ...................................................................................................... 46
8.3.2.1 Curriculum & Tasks ..............................................................................................................................46
8.3.3 Stage 3 : Manipulation ..................................................................................................... 46
8.3.3.1 Curriculum & Tasks ..............................................................................................................................46
8.4 DO, ASK, TAKEAWAY ........................................................................................................................ 47
8.5 ORGANIZATION AND ORDER ............................................................................................................... 49
8.5.1 Cut ups, Card Sorting, and David Bowie ............................................................................ 49
8.6 LESSON PLANS ................................................................................................................................ 50
9 PROGRAMMING AND UI .............................................................................................................. 50
9.1 INFORMAL AREAS ............................................................................................................................ 50
9.2 PROGRAMMING............................................................................................................................... 51
9.2.1 Architecture ...................................................................................................................... 51
9.2.2 Application Specifics ......................................................................................................... 52
9.2.2.1 Sound of Fractions Main Application ....................................................................................................52
9.2.2.2 SoF Data Viewer...................................................................................................................................53
9.2.2.3 Documentation and General Development Tools ..................................................................................53
9.2.3 Data Collection ................................................................................................................. 54
9.3 USER INTERFACE (UI) ....................................................................................................................... 54
9.3.1 Color ................................................................................................................................. 55
9.3.1.1 Our Color Choice ..................................................................................................................................55
9.3.1.2 Other Color Options .............................................................................................................................57
9.3.1.3 Color in Current Typical Mathematics Representations .........................................................................57
9.3.2 Stage ................................................................................................................................ 57
9.3.3 Representations ................................................................................................................ 57
9.3.3.1 Audio Representation ..........................................................................................................................59
9.3.3.2 Bead Representation............................................................................................................................60
9.3.3.3 Line Representation .............................................................................................................................60
9.3.3.4 Pie Representation...............................................................................................................................61
9.3.3.5 Bar Representation ..............................................................................................................................61
9.3.4 Transitions ........................................................................................................................ 62
9.3.5 Beats and Rests ................................................................................................................ 64
9.3.6 Playback ........................................................................................................................... 65
10 RESULTS ........................................................................................................................................ 65
10.1 DEMOGRAPHIC INFORMATION .......................................................................................................... 65
10.1.1 Census Data ................................................................................................................. 65
The Sound of Fractions
7
10.1.2 Education System Data ................................................................................................. 65
10.1.3 Student Demographic Data .......................................................................................... 66
10.1.4 Attendance and Participation ....................................................................................... 67
10.2 DATA SOURCES.............................................................................................................................. 67
10.3 THEMES PRESENT IN EACH DATA SOURCE ........................................................................................... 68
10.3.1 Evaluation of themes and data sources ......................................................................... 70
10.3.1.1 Themes, Concepts, and Perspectives ....................................................................................................70
10.3.1.2 Data Sources ........................................................................................................................................72
10.4 CURRICULUM ................................................................................................................................ 72
10.4.1 Group information ........................................................................................................ 73
10.4.1.1 Group 1 ...............................................................................................................................................75
10.4.1.2 Group 2 ...............................................................................................................................................75
10.4.2 Activities that students excelled at ................................................................................ 77
10.4.3 Activities that students struggled with .......................................................................... 77
10.5 LEARNING MOMENTS ..................................................................................................................... 77
10.5.1 Pre-post Test – What are fractions ................................................................................ 77
10.5.2 Student Explanations .................................................................................................... 77
10.5.3 Activities that students excelled at ................................................................................ 77
10.5.4 Activities that students struggled with .......................................................................... 77
11 DATA ORGANIZATION AND VISUALISATIONS ............................................................................... 78
11.1 VIDEO DATA ................................................................................................................................. 78
11.2 NOTEBOOKS AND ARTWORK DATA .................................................................................................... 80
11.3 LOG DATA .................................................................................................................................... 80
11.3.1 The distribution of rhythms made by students with a particular signature .................... 82
11.3.2 The distribution of recorded rhythms by duration ......................................................... 82
11.3.3 The comparison of rhythmic complexity against the number of beats tapped ............... 83
11.3.4 The number of instruments used in each rhythm........................................................... 84
11.3.5 The representations being visualized in each rhythm .................................................... 85
11.3.6 The number of times a rhythm was transitioned ........................................................... 86
11.3.7 Speeding Up versus Slowing Down ................................................................................ 86
12 DISCUSSION .................................................................................................................................. 88
12.1 RESEARCH QUESTIONS .................................................................................................................... 88
12.2 RESEARCH QUESTION 1: HOW CAN A MICRO-WORLD THAT UTILIZES ADDITIONAL REPRESENTATIONS PROVIDE
MEANINGFUL RESOURCES FOR LEARNING, AND ADDRESS MISCONCEPTIONS THAT ARE BLOCKING STUDENT LEARNING? . 88
12.2.1 Contexts in Math [Education] Domain .......................................................................... 88
12.2.1.1 Where Does Sound of Fractions Fit In ...................................................................................................89
12.2.1.2 Other Learning Contexts That Students Can Operate and Learn in .........................................................90
12.2.1.3 What SoF Supports ..............................................................................................................................93
12.2.2 Fractions, Representations, and Abstraction ................................................................. 93
12.3 RESEARCH QUESTION 2: CAN STUDENTS WHO STRUGGLE WITH FRACTIONS MAKE MEANINGFUL PROGRESS IN THEIR
COMPOSITION, COMPREHENSION, AND COMMUNICATION WHEN APPROACHING THE SYSTEM OF FRACTIONS FROM
PERSPECTIVES RELATED TO MUSIC? ............................................................................................................ 94
12.3.1 Hurdles Present in Students’ Misconceptions ................................................................ 94
12.3.1.1 n/n is confusing when n>20 ..................................................................................................................95
12.3.2 Reducing Complexity .................................................................................................... 96
12.3.2.1 Go Speed Racer Go! .............................................................................................................................97
12.3.3 What is the numerator?................................................................................................ 97
12.3.3.1 What happens to the size and fraction of the numerator as the whole changes? ...................................98
12.3.3.2 Which comes first? ..............................................................................................................................99
The Sound of Fractions
8
12.3.4 What is the denominator? .......................................................................................... 100
12.3.5 What is a fraction? ..................................................................................................... 101
12.3.5.1 pattern.map(function(Music||Math){ return Music ? Math : Music }) ................................................. 101
12.3.5.2 Descriptions and Definitions of Fractions as they Relate to SoF ........................................................... 102
12.4 RESEARCH QUESTION 3: HOW DO MULTIPLE, NOVEL, RICH, AND INTERACTIVE CULTURALLY APPROPRIATE
REPRESENTATIONS AFFECT ENGAGEMENT IN A LEARNING ENVIRONMENT? ........................................................ 103
12.4.1 Hey Mikey, I think s/he likes it! ................................................................................... 103
12.4.2 Multiple Representations ............................................................................................ 103
12.4.3 Novel Representations ................................................................................................ 103
12.4.4 Rich [mathematically oriented and musically related] Representations ....................... 104
12.4.5 Transitions.................................................................................................................. 104
12.4.6 Engagement as a whole.............................................................................................. 104
13 FUTURE WORK ........................................................................................................................... 105
13.1.1 Enhancements for additional studies .......................................................................... 105
13.1.2 Other Domains and Approaches ................................................................................. 105
14 CONCLUSION .............................................................................................................................. 105
15 APPENDIX ................................................................................................................................... 106
15.1 ABBREVIATIONS ........................................................................................................................... 106
15.2 ACCESSIBILITY OF THIS THESIS DOCUMENT ......................................................................................... 106
15.3 BLANK LESSON PLAN .................................................................................................................... 107
15.4 CURRICULUM .............................................................................................................................. 108
15.5 GROUP 1 VIDEO DATA AND NOTES .................................................................................................. 134
15.5.1 Group 1 Day 1 ............................................................................................................ 135
15.5.1.1 Group 1 Day 1 Activity 1 ..................................................................................................................... 135
15.5.1.2 Group 1 Day 1 Activity 2 (a and b)....................................................................................................... 136
15.5.1.3 Group 1 Day 1 Activity 3 ..................................................................................................................... 138
15.5.2 Group 1 Day 2 ............................................................................................................ 139
15.5.2.1 Group 1 Day 2 Activity 1 ..................................................................................................................... 139
Group 1 Day 2 Activity 2 ......................................................................................................................................... 140
15.5.2.2 Group 1 Day 2 Activity 3 ..................................................................................................................... 141
15.5.2.3 Group 1 Day 2 Activity 4 ..................................................................................................................... 142
15.5.3 Group 1 Day 3 ............................................................................................................ 143
15.5.3.1 Group 1 Day 3 Activity 1 ..................................................................................................................... 144
15.5.3.2 Group 1 Day 3 Activity 2 ..................................................................................................................... 145
15.5.3.3 Group 1 Day 3 Activity 3 ..................................................................................................................... 146
15.5.3.4 Group 1 Day 3 Activity 4 ..................................................................................................................... 147
15.5.3.5 Group 1 Day 3 Activity 5 ..................................................................................................................... 148
15.5.4 Group 1 Day 4 ............................................................................................................ 149
15.5.4.1 Group 1 Day 4 Activity 1 ..................................................................................................................... 150
15.5.4.2 Group 1 Day 4 Activity 2 ..................................................................................................................... 151
15.5.4.3 Group 1 Day 4 Activity 3 ..................................................................................................................... 152
15.5.4.4 Group 1 Day 4 Activity 4 ..................................................................................................................... 153
15.5.5 Group 1 Day 5 ............................................................................................................ 154
15.5.5.1 Group 1 Day 5 Activity 1 ..................................................................................................................... 155
15.5.5.2 Group 1 Day 5 Activity 2 ..................................................................................................................... 156
15.5.5.3 Group 1 Day 5 Activity 3 ..................................................................................................................... 157
15.5.6 Group 1 Day 6 ............................................................................................................ 158
15.5.6.1 Group 1 Day 6 Activity 1 ..................................................................................................................... 159
15.5.6.2 Group 1 Day 6 Activity 2 ..................................................................................................................... 160
15.5.7 Group 1 Day 7 ............................................................................................................ 161
15.5.7.1 Group 1 Day 7 Activity 1 ..................................................................................................................... 162

The Sound of Fractions
9
15.5.7.2 Group 1 Day 7 Activity 2 ..................................................................................................................... 163
15.5.7.3 Group 1 Day 7 Activity 3 ..................................................................................................................... 164
15.6 GROUP 2 VIDEO DATA AND NOTES .................................................................................................. 165
15.6.1 Group 2 Day 1 ............................................................................................................ 166
15.6.1.1 Group 2 Day 1 Activity 1 ..................................................................................................................... 167
15.6.1.2 Group 2 Day 1 Activity 2 (a and b)....................................................................................................... 168
15.6.1.3 Group 2 Day 1 Activity 3 ..................................................................................................................... 170
15.6.1.4 Group 2 Day 1 Activity 4 ..................................................................................................................... 171
15.6.2 Group 2 Day 2 ............................................................................................................ 172
15.6.2.1 Group 2 Day 2 Activity 1 ..................................................................................................................... 173
15.6.2.2 Group 2 Day 2 Activity 2 ..................................................................................................................... 174
15.6.2.3 Group 2 Day 2 Activity 3 ..................................................................................................................... 175
15.6.2.4 Group 2 Day 2 Activity 4 ..................................................................................................................... 176
15.6.3 Group 2 Day 3 ............................................................................................................ 177
15.6.3.1 Group 2 Day 3 Activity 1 ..................................................................................................................... 178
15.6.3.2 Group 2 Day 3 Activity 2 ..................................................................................................................... 179
15.6.3.3 Group 2 Day 3 Activity 3 ..................................................................................................................... 180
15.6.4 Group 2 Day 4 ............................................................................................................ 181
15.6.4.1 Group 2 Day 4 Activity 1 ..................................................................................................................... 181
15.6.4.2 Group 2 Day 4 Activity 2 ..................................................................................................................... 182
15.6.4.3 Group 2 Day 4 Activity 3 ..................................................................................................................... 183
15.6.5 Group 2 Day 5 ............................................................................................................ 184
15.6.5.1 Group 2 Day 5 Activity 1 ..................................................................................................................... 185
15.6.5.2 Group 2 Day 5 Activity 2 ..................................................................................................................... 186
15.6.5.3 Group 2 Day 5 Activity 3 ..................................................................................................................... 187
15.6.6 Group 2 Day 6 ............................................................................................................ 188
15.6.6.1 Group 2 Day 6 Activity 1 ..................................................................................................................... 188
15.6.6.2 Group 2 Day 6 Activity 2 ..................................................................................................................... 189
15.7 MAIN CODE BRANCH DEVELOPMENT TIMELINE VIDEO ......................................................................... 190
15.8 INSTITUTIONAL REVIEW BOARD CERTIFICATION .................................................................................. 191
15.9 INDIRECT REFERENCES ................................................................................................................... 192
15.10 ADDITIONAL THOUGHTS FROM THE AUTHOR .................................................................................... 203
16 BIBLIOGRAPHY ........................................................................................................................... 204
1 LIST OF TABLES
TABLE 5-1 : COMMON CORE TOPICS COVERED IN MATH CURRICULUM FOR GRADES K-8.............................................................. 15
TABLE 10-1 EDUCATION SYSTEM DATA OF THE NUMBER OF STUDENTS, AND THE PERCENTAGE ON FREE AND REDUCED LUNCH .............. 66
TABLE 10-2 STUDENT DEMOGRAPHIC INFORMATION OF THE TWO GROUPS ............................................................................. 67
TABLE 10-3 SECTION A OF THEMES, CONCEPTS, AND PERSPECTIVES PRESENT IN EACH DATA SOURCE .............................................. 69
TABLE 10-4 SECTION B OF THEMES PRESENT IN EACH DATA SOURCE. A STRONG RATING EQUALS 3 POINTS, A MEDIUM RATING EQUALS
2 POINTS, A WEAK RATING EQUALS 1, AND 0 POINTS ARE ASSIGNED TO DATA THAT DOES NOT SHOW EVIDENCE OF BEING PRESENT
WITH -. THE TOTALS ARE TALLIED VERTICALLY FOR EACH DATA SOURCE, AND HORIZONTALLY FOR EACH THEME. ........................ 70
TABLE 10-5 WEIGHTED RATINGS OF A HIGHER LEVEL PERSPECTIVES AND THEIR UNDERLYING CONCEPTS PER EACH DATA SOURCE. ......... 72

The Sound of Fractions
10
2 LIST OF FIGURES
FIGURE 1-1 THIS IS THE LEFT PAGE, BEHIND THE MAIN COVER PAGE, INTENDED TO FUNNY, AND NOT BLANK: ABOVE:
HTTP://PLUS5MACE.TUMBLR.COM/IMAGE/9924002940 BELOW: HTTP://ARSENIIC.DEVIANTART.COM/ART/WHAT-DO-YOU-
CALL-AN-ALLIGATOR-IN-A-VEST-288568405 ........................................................................................................... 2
FIGURE 5-1 COMMON MISTAKES STUDENTS MAKE IN MATH ......................................................................................... 16
FIGURE 5-2 THE SPLITTING LOOPE SCHEMES ACCORDING TO NORTON AND WILKINS (2013) ................................................ 19
FIGURE 8-1 A BLANK ACTIVITY SHEET THAT FOLLOWS THE DO, ASK, TAKEAWAY MODEL. IT HAS AREAS FOR MATERIALS, SETUP, NOTES FOR
THE FACILITATOR, LOCATION, DAY, ACTIVITY NUMBER, PROJECTED DURATION, A, THE NAME OF THE ACTIVITY, AND THE ASSOCIATED
SOL THEMES AND COMPONENTS ......................................................................................................................... 48
FIGURE 8-2 AN EXAMPLE OF AN ACTIVITY PRIOR TO BEING COMPLETE, WITH SECTIONS FOR DO, ASK, TAKEAWAY, SUPPLIES, AND GENERAL
NOTES ........................................................................................................................................................... 49
FIGURE 8-3 MOST ACTIVITIES ON A TEMPORARILY TAPED ON A DRY ERASE BOARD TO ALLOW FOR MOVING AROUND, CATEGORIZATION,
ORDER, AND EDITING DURING THE FINAL STAGES OF PLAANING FOR THE OVERALL CURRICULUM AND LESSON PLANS. .................. 50
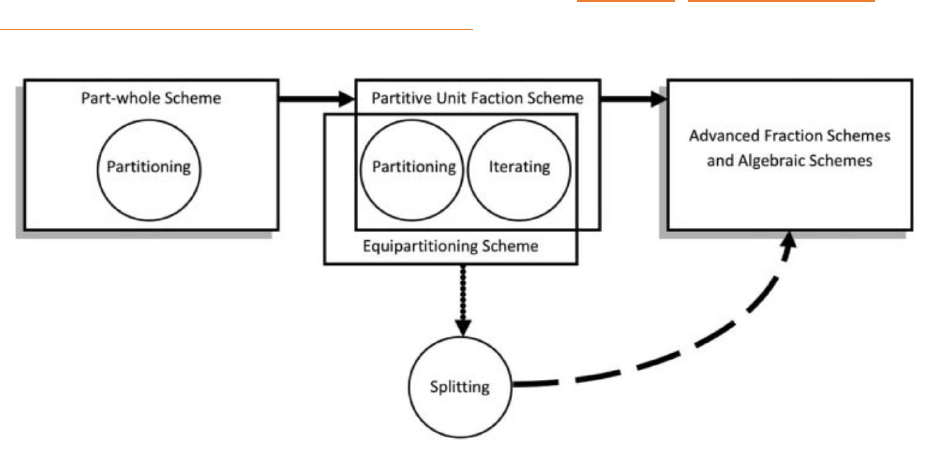
FIGURE 9-1 THE FINAL UI DESIGN OF SOF WITH A SNARE INSTRUMENT WITH 5 ALTERNATING BEATS, A HIGH HAT WITH 4 ALTERNATING
BEATS, AN UNUSED KICK DRUM, AND BOTH USED INSTRUMENTS HAVING ALL 5 REPRESENTATIONS PRESENT, CURRENTLY NOT
PLAYING/ANIMATING. ....................................................................................................................................... 55
FIGURE 9-2 THE COLOR PALETTE OF BEATS IN ORDER 1 THROUGH 16 ..................................................................................... 56
FIGURE 9-3 THE AUDIO REPRESENTATION PRESENT IN SOF ................................................................................................. 59
FIGURE 9-4 THE BEAD REPRESENTATION PRESENT IN SOF ................................................................................................... 60
FIGURE 9-5 THE LINE REPRESENTATION PRESENT IN SOF ..................................................................................................... 60
FIGURE 9-6 THE PIE REPRESENTATION PRESENT IN SOF ...................................................................................................... 61
FIGURE 9-7 THE BAR REPRESENTATION PRESENT IN SOF ..................................................................................................... 61
FIGURE 9-8 A COMPARISON OF THE REPRESENTATIONS AND THEIR TRANSITIONS WITH RELATIVE PROPERTIES ............................. 63
FIGURE 9-9 UNROLLING A CIRCLE INTO A LINE WITH FEWER FRAMES AND LESS REFERENCE POINTS. ................................................ 64
FIGURE 10-1 OVERVIEW OF BOTH GROUPS STUDY SESSIONS, INCLUDING THE OVERALL ELAPSED TIME OF THE DAY AND INDIVIDUAL TIMES
FOR ACTIVITIES ................................................................................................................................................ 76
FIGURE 11-1 A LEGEND OF THE STRUCTURE OF DATA OF THE VIDEO ANALYSIS OF EACH ACTIVITY OF EACH DAY OF A EACH GROUP,
INCLUDING STUDENTS, SUB ACTIVITIES, CONTRIBUTIONS, AND GENERAL NOTES, WITH NOTATIONS OF ACCOMPANYING DIARY
ENTRIES. ........................................................................................................................................................ 79
FIGURE 11-2 DISTRIBUTION OF RHYTHMS BY SIGNATURE .................................................................................................... 82
FIGURE 11-3 DISTRIBUTION OF RECORDED RHYTHMS BY DURATION ....................................................................................... 83
FIGURE 11-4 THE COMPARISON OF RHYTHMIC COMPLEXITY AGAINST THE NUMBER OF BEATS TAPPED ............................................. 84
FIGURE 11-5 THE NUMBER OF INSTRUMENTS USED IN EACH RHYTHM ..................................................................................... 85
FIGURE 11-6 THE REPRESENTATIONS BEING VISUALIZED IN EACH RHYTHM ............................................................................... 85
FIGURE 11-7 THE NUMBER OF TIMES A RHYTHM WAS TRANSITIONED ..................................................................................... 86
FIGURE 11-8 SPEEDING UP VS SLOWING DOWN RHYTHMS ................................................................................................. 87
FIGURE 11-9 RHYTHM DURATION SCALED IN TERMS OF ORIGINAL DURATION IN TERMS OF X ........................................................ 87
FIGURE 12-1 THE SYSTEM OF FRACTIONS AND ITS MAJOR COMPONENTS ON THE LEFT. A REPRESENTATION OF HOW THE MATH DOMAIN IS
CURRENTLY REPRESENTED, IMPLEMENTED, AND MEASURED ON THE RIGHT, WITH THE SOUND OF FRACTIONS UNSURE OF HOW TO
PROPERLY FIT IN THE MATH DOMAIN. .................................................................................................................... 90
FIGURE 12-2 BY INTRODUCING A WHOLLY DIFFERENT APPROACH TO FRACTION LEARNING (PARTICULARLY USING AURAL AND EMBODIED
COMPONENTS) WE NOTICED THAT OTHER CONTEXTS EXIST TO TEACH FRACTIONS WITH. THESE WERE CONFIRMED BY STUDENTS
DURING THE STUDY, AS WELL AS OTHER CONTEXTS WERE GIVEN AS EXAMPLES BY STUDENTS (GUSTATORY) DURING DISCUSSION AND
INTERACTIONS. THIS LED US TO CONSIDER HOW MATH IS REPRESENTED IN DIFFERENT CONTEXTS, THEIR AFFORDANCES AND
WEAKNESSES, AND WHAT CONTEXTS PROVIDE STRONG AND MEANINGFUL LEARNING OPPORTUNITIES WITH FEWER MISCONCEPTIONS
AND DIFFICULTY WHEN LEARNING FRACTIONS. ......................................................................................................... 92
FIGURE 12-3 THE CONTEXTS, REPRESENTATIONS, AND PERFORMANCES THAT SOF ENGAGES AND CHALLENGES STUDENTS IN, SUPPORTS VIA
THE CURRICULUM AND SOCIO-TECHNICAL INTERFACE, AND OPERATES WITHIN A DYNAMIC ENVIRONMENT TO SUPPORT DIFFERENT
STUDENTS’ APPROACHES. ................................................................................................................................... 93
FIGURE 12-4 THE WHITEBOARD SHOWING THE BEAD AND THE PIE REPRESENTATIONS (CHOSEN BY THE STUDENTS AS PREFERABLE TO WORK
WITH) BEFORE AND AFTER DOUBLING THE SIZE OF THEM. THE PIE REPRESENTATION PREVIOUSLY (SHOWN IN THE BOTTOM RIGHT)
WAS DIVIDED INTO 11 EQUAL PARTS, BUT ONLY OCCUPYING 50% OF THE DOUBLED CIRCLE. THE NUMBER OF ITERATED PARTS
The Sound of Fractions
11
(MADE BY THE STUDENTS) EQUALED THE SMALLER CIRCLE, BUT THE DESIGN WAS STARKLY DIFFERENT AND REQUIRED REWORKING TO
ENSURE THAT THE UNIT FRACTION REMAINED THE SAME AFTER THE WHOLE (RHYTHM) WAS DOUBLED (IN DURATION). ............... 99
FIGURE 15-1 : THE LESSON PLAN PLANNING PAGE. THIS ALLOWS RESEARCHERS TO IDENTIFY THE MEANINGFUL COMPONENTS OF A WELL
DESIGNED LESSON AND COMMUNICATE THEM EASILY FOR A TEACHER TO REVIEW AND REFERENCE DURING A CLASS SESSION. ..... 107
FIGURE 15-2 WHAT DO FRACTIONS MEAN TO YOU? - LESSON PLAN DAY 1, ACTIVITY 1 ........................................................... 108
FIGURE 15-3 LISTENING TO A RHYTHM - LESSON PLAN DAY 1, ACTIVITY 2 ............................................................................ 109
FIGURE 15-4 MAKE YOUR OWN RHYTHM AND REPRESENTATION - LESSON PLAN DAY 1, ACTIVITY 3 ............................................ 110
FIGURE 15-5 MAKE A NEW REPRESENTATION - LESSON PLAN DAY 1, ACTIVITY 4 .................................................................... 111
FIGURE 15-6 DAY 1 HOMEWORK PATTERNS - LESSON PLAN DAY 1, HOMEWORK ................................................................... 112
FIGURE 15-7 DESCRIBE WHAT'S IMPORTANT - LESSON PLAN DAY 2, ACTIVITY 1 .................................................................... 113
FIGURE 15-8 MIMICKING RHYTHMS - LESSON PLAN DAY 2, ACTIVITY 2 ............................................................................... 114
FIGURE 15-9 WHAT SIZE!? - LESSON PLAN DAY 2, ACTIVITY 3 .......................................................................................... 115
FIGURE 15-10 THE MEDICAL REPRESENTATIONS HANDOUT - LESSON PLAN DAY 2, ACTIVITY 3.................................................. 116
FIGURE 15-11 MAKE YOUR OWN FRACTION REPRESENTATION - LESSON PLAN DAY 2, ACTIVITY 4 ............................................... 117
FIGURE 15-12 THE NUMBERS REPRESENTATION HANDOUT - LESSON PLAN DAY 2, ACTIVITY 4 ................................................... 118
FIGURE 15-13 PLAY WITH SOF - LESSON PLAN DAY 2, ACTIVITY 5 ...................................................................................... 119
FIGURE 15-14 DAY 2 HOMEWORK ............................................................................................................................. 120
FIGURE 15-15 MAKE A BEAD REPRESENTATION - LESSON PLAN DAY 3, ACTIVITY 1 ................................................................. 121
FIGURE 15-16 TAP IN YOUR RHYTHM - LESSON PLAN DAY 3, ACTIVITY 2 .............................................................................. 122
FIGURE 15-17 WHAT IS A WHOLE - LESSON PLAN DAY 3, ACTIVITY 3 .................................................................................. 123
FIGURE 15-18 DAY 3 HOMEWORK ............................................................................................................................. 124
FIGURE 15-19 ALL THE REPRESENTATIONS! - LESSON PLAN DAY 4, ACTIVITY 1 ...................................................................... 125
FIGURE 15-20 THE OTHER PART - LESSON PLAN DAY 4, ACTIVITY 2 .................................................................................... 126
FIGURE 15-21 WHICH COMES FIRST? - LESSON PLAN DAY 4, ACTIVITY 3 .............................................................................. 127
FIGURE 15-22 DAY 4 HOMEWORK ............................................................................................................................. 128
FIGURE 15-23 RECAP - LESSON PLAN DAY 5, ACTIVITY 1.................................................................................................. 129
FIGURE 15-24 BEADS VS LINES - LESSON PLAN DAY 5, ACTIVITY 2 ...................................................................................... 130
FIGURE 15-25 ORDERING YOUR RHYTHM - LESSON PLAN DAY 5, ACTIVITY 3 ......................................................................... 131
FIGURE 15-26 IDENTIFY AND LABEL WHAT IS IMPORTANT - LESSON PLAN DAY 6, ACTIVITY 1 ..................................................... 132
FIGURE 15-27 TRANSITIONING TO OTHER REPRESENTATIONS - LESSON PLAN DAY 6, ACTIVITY 2 ................................................ 133
FIGURE 15-28 A LEGEND AND DESCRIPTION FOR REVIEWING VIDEO DATA OF ACTIVITIES AND SUB-ACTIVITIES ................................. 134
FIGURE 15-29 AN OVERVIEW OF GROUP 1 DAY 1 CLASSROOM VIDEO DATA ......................................................................... 135
FIGURE 15-30 GROUP 1 DAY 1 ACTIVITY 1 CLASSROOM VIDEO DATA .................................................................................. 135
FIGURE 15-31 GROUP 1 DAY 1 ACTIVITY 2A CLASSROOM VIDEO DATA ................................................................................ 136
FIGURE 15-32 GROUP 1 DAY 1 ACTIVITY 2B CLASSROOM VIDEO DATA ................................................................................ 137
FIGURE 15-33 GROUP 1 DAY 1 ACTIVITY 3 VIDEO DATA ................................................................................................... 138
FIGURE 15-34 GROUP 1 DAY 2 OVERVIEW CLASSROOM VIDEO DATA .................................................................................. 139
FIGURE 15-35 GROUP 1 DAY 2 ACTIVITY 1 CLASSROOM VIDEO DATA .................................................................................. 139
FIGURE 15-36 GROUP 1 DAY 2 ACTIVITY 2 CLASSROOM VIDEO DATA .................................................................................. 140
FIGURE 15-37 GROUP 1 DAY 2 ACTIVITY 3 CLASSROOM VIDEO DATA .................................................................................. 141
FIGURE 15-38 GROUP 1 DAY 2 ACTIVITY 4 CLASSROOM VIDEO DATA .................................................................................. 142
FIGURE 15-39 GROUP 1 DAY 3 OVERVIEW CLASSROOM VIDEO DATA .................................................................................. 143
FIGURE 15-40 GROUP 1 DAY 3 ACTIVITY 1 CLASSROOM VIDEO DATA .................................................................................. 144
FIGURE 15-41 GROUP 1 DAY 3 ACTIVITY 2 CLASSROOM VIDEO DATA .................................................................................. 145
FIGURE 15-42 GROUP 1 DAY 3 ACTIVITY 3 CLASSROOM VIDEO DATA .................................................................................. 146
FIGURE 15-43 GROUP 1 DAY 3 ACTIVITY 4 CLASSROOM VIDEO DATA .................................................................................. 147
FIGURE 15-44 GROUP 1 DAY 3 ACTIVITY 5 CLASSROOM VIDEO DATA .................................................................................. 148
FIGURE 15-45 GROUP 1 DAY 4 OVERVIEW CLASSROOM VIDEO DATA .................................................................................. 149
FIGURE 15-46 GROUP 1 DAY 4 ACTIVITY 1 CLASSROOM VIDEO DATA .................................................................................. 150
FIGURE 15-47 GROUP 1 DAY 4 ACTIVITY 2 CLASSROOM VIDEO DATA .................................................................................. 151
FIGURE 15-48 GROUP 1 DAY 4 ACTIVITY 4 ................................................................................................................... 153
FIGURE 15-49 GROUP 1 DAY 5 OVERVIEW CLASSROOM VIDEO DATA .................................................................................. 154
FIGURE 15-50 GROUP 1 DAY 5 ACTIVITY 1 CLASSROOM VIDEO DATA .................................................................................. 155

The Sound of Fractions
12
FIGURE 15-51 GROUP 1 DAY 5 ACTIVITY 2 CLASSROOM VIDEO DATA .................................................................................. 156
FIGURE 15-52 GROUP 1 DAY 5 ACTIVITY 3 CLASSROOM VIDEO DATA .................................................................................. 157
FIGURE 15-53 GROUP 1 DAY 6 OVERVIEW CLASSROOM VIDEO DATA .................................................................................. 158
FIGURE 15-54 GROUP 1 DAY 6 ACTIVITY 1 CLASSROOM VIDEO DATA .................................................................................. 159
FIGURE 15-55 GROUP 1 DAY 6 ACTIVITY 2 CLASSROOM VIDEO DATA .................................................................................. 160
FIGURE 15-56 GROUP 1 DAY 7 OVERVIEW CLASSROOM VIDEO DATA .................................................................................. 161
FIGURE 15-57 GROUP 1 DAY 7 ACTIVITY 1 CLASSROOM VIDEO DATA .................................................................................. 162
FIGURE 15-58 GROUP 1 DAY 7 ACTIVITY 2 CLASSROOM VIDEO DATA .................................................................................. 163
FIGURE 15-59 GROUP 1 DAY 7 ACTIVITY 3 CLASSROOM VIDEO DATA .................................................................................. 164
FIGURE 15-60 A LEGEND AND DESCRIPTION FOR REVIEWING VIDEO DATA OF ACTIVITIES AND SUB-ACTIVITIES ................................. 165
FIGURE 15-61 GROUP 2 DAY 1 OVERVIEW CLASSROOM VIDEO DATA .................................................................................. 166
FIGURE 15-62 GROUP 2 DAY 1 ACTIVITY 1 CLASSROOM VIDEO DATA .................................................................................. 167
FIGURE 15-63 GROUP 2 DAY 1 ACTIVITY 2A CLASSROOM VIDEO DATA ................................................................................ 168
FIGURE 15-64 GROUP 2 DAY 1 ACTIVITY 2B CLASSROOM VIDEO DATA ................................................................................ 169
FIGURE 15-65 GROUP 2 DAY 1 ACTIVITY 3 CLASSROOM VIDEO DATA .................................................................................. 170
FIGURE 15-66 GROUP 2 DAY 1 ACTIVITY 4 CLASSROOM VIDEO DATA .................................................................................. 171
FIGURE 15-67 GROUP 2 DAY 2 OVERVIEW CLASSROOM VIDEO DATA .................................................................................. 172
FIGURE 15-68 GROUP 2 DAY 2 ACTIVITY 1 CLASSROOM VIDEO DATA .................................................................................. 173
FIGURE 15-69 GROUP 2 DAY 2 ACTIVITY 2 CLASSROOM VIDEO DATA .................................................................................. 174
FIGURE 15-70 GROUP 2 DAY 2 ACTIVITY 3 CLASSROOM VIDEO DATA .................................................................................. 175
FIGURE 15-71 GROUP 2 DAY 2 ACTIVITY 4 CLASSROOM VIDEO DATA .................................................................................. 176
FIGURE 15-72 GROUP 2 DAY 3 OVERVIEW CLASSROOM VIDEO DATA .................................................................................. 177
FIGURE 15-73 GROUP 2 DAY 3 ACTIVITY 1 CLASSROOM VIDEO DATA .................................................................................. 178
FIGURE 15-74 GROUP 2 DAY 3 ACTIVITY 2 CLASSROOM VIDEO DATA .................................................................................. 179
FIGURE 15-75 GROUP 2 DAY 3 ACTIVITY 3 VIDEO DATA ................................................................................................... 180
FIGURE 15-76 GROUP 2 DAY 4 OVERVIEW CLASSROOM VIDEO DATA .................................................................................. 181
FIGURE 15-77 GROUP 2 DAY 4 ACTIVITY 1 CLASSROOM VIDEO DATA .................................................................................. 181
FIGURE 15-78 GROUP 2 DAY 4 ACTIVITY 2 CLASSROOM VIDEO DATA .................................................................................. 182
FIGURE 15-79 GROUP 2 DAY 4 ACTIVITY 3 VIDEO DATA ................................................................................................... 183
FIGURE 15-80 GROUP 2 DAY 5 OVERVIEW VIDEO DATA ................................................................................................... 184
FIGURE 15-81 GROUP 2 DAY 5 ACTIVITY 1 CLASSROOM VIDEO DATA .................................................................................. 185
FIGURE 15-82 GROUP 2 DAY 5 ACTIVITY 2 CLASSROOM VIDEO DATA .................................................................................. 186
FIGURE 15-83 GROUP 2 DAY 5 ACTIVITY 3 VIDEO DATA ................................................................................................... 187
FIGURE 15-84 GROUP 2 DAY 6 OVERVIEW CLASSROOM VIDEO DATA .................................................................................. 188
FIGURE 15-85 GROUP 2 DAY 6 ACTIVITY 1 CLASSROOM VIDEO DATA .................................................................................. 188
FIGURE 15-86 GROUP 2 DAY 6 ACTIVITY 2 CLASSROOM VIDEO DATA .................................................................................. 189
FIGURE 15-87 A VIDEO RENDERING OF A FORCE DIRECTED LAYOUT OF THE MASTER BRANCH DEVELOPMENT OF CODE FOR THE SOUND OF
FRACTIONS. ALSO VIEWABLE AT HTTPS://YOUTU.BE/FSM2UKWS2VS........................................................................ 190
FIGURE 15-88 : IRB CERTIFICATE PAGE ....................................................................................................................... 192
3 ABSTRACT
Learning fractions is the focus for much of elementary school mathematics instruction
because it is important and can be difficult. Fractions constitute a system of thinking about

The Sound of Fractions
13
numbers and representations that differs in important ways from counting numbers. To
understand fractions requires, for example, perceiving that a symbol such as “6” is not
automatically associated with a larger quantity than “5” if they are denominators. In the
system that constitutes fractions, 1/5 is bigger than 1/6. When students fail to master the
system of fractions by a certain age, the inherent difficulty of the concepts can become
confounded with discouragement, boredom, and humiliation. Music, especially percussion,
not only provides an engaging context for many students but musical patterning can also
provide deep analogic experiences to fractions at embodied and representational levels.
Reasonable questions about musical patterns can both motivate and guide students towards
understanding the properties of systems of fractions and their representations. We utilize this
possibility in a new tool and associated curriculum called Sound of Fractions (SoF). SoF
incorporates three main ideas to leverage musical interest and skill to provide an alternative
approach to teaching fractions:
1. Experiencing the whole and the part at the same time is crucial to learning fractions;
2. Drumming is a compelling, embodied, culturally-relevant activity that allows students to
experience the wholes, the parts, and the relationships between them at the same time;
3. A new computer-based representational infrastructure utilizing aural, visual, physical,
and temporal components that scaffolds classroom-based activities that bridge the
relationship between percussion-related and mathematics activities in such a way as to
gradually bring the student towards more standard mathematical representations and
usages.
We conducted preliminary testing of this approach in two series of after school programs with
5
th
-8
th
grade children who were significantly behind in learning fractions. Preliminary
indications are that the approach is promising and ready to be tried in more formal contexts.
This work illustrates that instruction rich in representational infrastructure and domains
continues to be an important component of how technology can have positive impact.
4 INTRODUCTION
Fractions are arguably the most important topic in upper-elementary mathematics.
Furthermore, they are surprisingly difficult to learn. For this reason, there is a large body of
literature in the learning sciences and in mathematics educations exploring early
conceptualization and approaches to teaching (Panel, 2008). In the United States (US), the
struggle to learn fractions is ``pervasive and an obstacle to further progress in mathematics and
other domains'' and can have detrimental effects on adulthood, including failure to
comprehend medication regimens (Panel, 2008). The difficulties that many children experience
while learning fractions are compounded when the children live in situations of high poverty,
attend low-performing schools, have personal experiences of failure, and succumb to boredom
with what appears to be repeated presentations of the same material (Empson & Levi, 2011).
When we observed students struggling with fractions in the classroom we noticed some
children's reaction to their teacher's instruction, where students were tapping on their desk
using fingers and pencils. We used this as a possible design pathway to offer a different

The Sound of Fractions
14
instructional path, one that began with music, an area of interest for students as well as an area
related to mathematics.
We identified the important parts of successful learning by running small sequential studies and
design sessions, and created a comprehensive curriculum to approach fractions through the
lens of music. We used the foremost math learning strategies, leveraged the students’ interest
in music, designed novel representations with inspiration from traditional math learning
resources, and organized them into a new socio-technical web application that is strengthened
by activities both on and off the computer. This new approach, although rather different in
many facets, is actually a stronger approach to learning, as it abandons standardized testing
and the accompanying teaching rubrics. Our robust approach also supports children’s interests
towards learning fractions and mathematics more so than the current learning environment
that they are underperforming in.
We ran two sessions of this study with 8 and 12 students over 7 weeks. We began by allowing
the students to explore music and making representations of rhythmic performances,
highlighting the important components of the rhythm when considering them in a different
representational form. Our curriculum then allows students to perform rhythms individually
and collectively in an environment that undergirds embodied interactions before introducing
them to SoF, which then adds additional rich visual representations. Each stage is carefully
planned so that students progress from creation to identification, followed by manipulation of
rhythms. This allows students to be able to contextualize, identify, quantify, iterate, separate,
and order the unit fractions, parts, whole(s), and the relationship of the parts and wholes as
they interact with the system of fractions in different domains.
5 LITERATURE REVIEW
Math education has a tremendous amount of research covering curriculum topics,
technique, and order of topic presentations (Empson & Levi, 2011; Initiative & others, 2012;
Anderson Norton & Wilkins, 2009). Music educators follow a separate set of influences in
educating students. Computer Science, a major influence in the history of this research, also
has many thoughts about education, instruction, and topic discussion. In this section we
discuss the wealth of research that we cover in our research efforts.
5.1 Common Themes in Mathematical Instruction
Education in the US varies from state to state, from county to county, and in some cases, from
city to city. The diversity of education services and resources has a strong impact on districts
that already struggle to offer both the best and equal services for all students across schools
within the district. One growing method adopted by districts for consistent curriculum is the
Common Core (CC) (Initiative & others, 2012). The CC concretely suggests what should be
known by all K-12 students upon completing a particular grade, barring any particular hindering
learning disability. States are typically left with how to qualify students’ knowledge of the CC
milestones. Districts and schools, however, are left to decide what curriculum and tools to use
The Sound of Fractions
15
to meet these standards, and also how to handle students who do not meet the CC guidelines.
Grade retention, a common choice by administrators for students falling behind, is on the rise
since the 1970s (Gamoran, 2007), and sometimes applied to a specific course despite
progressing the student on to the next grade. This segmented and abstracted hierarchical
structure leaves too much distance between those that teach and those that assess, and adds
layers of complexity when teachers are left to decide how to approach learning in a meaningful
way to their classrooms as a whole and students as an individual, and has been criticized by
other country’s scholars who have a high literacy rate in mathematics (Salsberg, 2014).
In regards to math, the CC begins to introduce fractions in grade 3 (~8 years old), by
familiarizing students to the idea of identifying numbers by their amount/size (via location on
the number line), whole numbers in fraction form, and equivalence (same location on a number
line)(Initiative & others, 2012). A brief simplification of the CC’s approach to fractions shows
the following progression from representations (fraction, decimal, percentage) to more
integrated math schemes in Table 5-1:
Common Core Math Levels
Grade
~Age
(years)
Topics covered
K
5
Counting, Cardinality, Shapes, Measurement
1
6
Operations (add, subtract), Base 10,
2
7
Standard units, place value, foundation for multiplication/division
3
8
Operations (multiple, divide), fractions as numbers, unit fractions
4
9
Fractions, decimals, and percentage representations, equivalence and
ordering
5
10
Multiplication and division of fractions
6
11
Variables, ratios, and proportions
7
12
Applying equations to geometry, rates, and more integrated math schemes
8
13
Use equations and expressions to form higher order functions and statistics
Table 5-1 : Common Core topics covered in math curriculum for grades K-8

The Sound of Fractions
16
The complexity of mathematical language students are expected to master grows with
each grade. Thus, there is a clear need to understand a previous grade level's concepts prior to
progressing to the next level. This structure is flawed in its motivation to undergird
progression, highlighted by the lack of guidance for students who fall behind. The current
typical response for schools, administration, and teachers is to have the students repeat the
class or curriculum, and in some cases develop severely delayed individual development plans
of the same curriculum with no variance in instructional design or presentation. This
unaddressed area is a tenant of our approach.
The students who are failing to pass the tests given to them are not aware of their failing other
than the feedback from the numerical or alphabetical grade returned to them. Since students
fail to understand the concepts that underpin the system of fractions, they fail to see their
mistakes, evidenced by their grade. Rather, students attempt to make sense of the various
mnemonics, rules, shortcuts, and sing-a-long memorization strategies that are presented to
them over time [XXX-Citation Needed and reference this phenomenon later with the ‘COPY-
Flip-Change discussion between the Muhammed and Giada at Group 1]. The problem of this
mechanism is that they continually add more `helping tools' without understanding the flaws of
their current structure. In Figure 5-1 (Common mistakes students make in math), students
know they have to add the numerator when adding, but don't understand you can only do this
when they are of equal sizes, so they also add the denominator. When multiplying in long
division style, students know that alignment is important, but forget what to align (e.g. align to
the left, align to the right, align the decimals or align the last digit). The difficulties may be
traced to simple arithmetic as well, when students continue to persist when `borrowing'.
Figure 5-1 Common mistakes students make in math
This problematic area of how to help remedial math students is a focus of our approach.
Starting from an approachable and attractive area of music allows remedial students to begin
to use their musical skills to understand the system of fractions they are already exposed to, yet
not having clear or productive interactions with and are unaware of their common mistakes.
The Sound of Fractions
17
5.2 Common Themes in Musical Instruction
The curriculum for musical education in elementary school grades follows a very similar
time schedule as mathematical education. However, unlike math education, music education
begins with basic vocabulary and guided imitation. Students then progress to use more
descriptive vocabulary to address the increased difficulty, wider range of musical performance,
collaboration with other students who play the same instrument, and the complexities of
playing with other musicians in an organized manner. The novice-level vocabulary words
describe (although not completely exact, robust, or distinguishable) the characteristics of the
sounds, such as tone, pitch, frequency, or their associated name (e.g. A♭, A, and A#, ...). Other
words are reserved for describing the mechanics, such as measure, beat, rest, and tempo.
Some describe the length and duration, such as whole note, whole rest, half [note/rest],
quarter [note/rest], eight [note/rest], 16th, 32nd, and 64
th
, but require knowledge of the tempo
(120 beats per minute, 180 beats per minute, 240 bpm, …), and the signature, such as 4/4,
common time, or more complex signatures to know the exact length in time. There may even
be discussion about the performance, including, staccato (playing the the sound sharply with
distinguishable separation from the next note), crescendo (XXX), allegro (XXX), and other
distinguishable actions. As students develop their musical talent, the teacher (who is
sometimes a professional conductor who teaches) begins to use a language that goes beyond
the elementary vocabulary, mimicking, or rote repetitive call and answer. This language uses
more abstract thoughts and allegories, such as one conductor used to describe a staccato
rhythm, ``these little accents... ...it's as if a little cat came in to touch you'' (Barten, 1992).
The differences between how to teach math and music reveal varied emphasis on
progression from simple to complex mental events and novice-level practice of the subject
matter. How to teach math is dependent on a multi-tiered progression of complexity, a student
starts at the arguably simpler concepts of amount and size and must construct the cognitive
steps necessary to climb to the next level of complexity. In comparison, how to teach music
depends on a similar progression from simple to more complex activities, but this process is
mitigated with novice-level strategies like imitation, mimicking, and rote repetitive call and
answer that collectively and consistently reinforce each other. A student in math can grasp
multiplication without understanding other mathematical properties (such as it being the
inverse of division, or the same as repeated addition). This is different than a student playing a
small piece twice as fast without being able to preserve other characteristics of the musical
piece (the relation of the spacing of the beats to the musical piece [whole] being the same, but
the sound being different). Said differently, to progress in in either domain requires well
rounded and intricate knowledge of relationships and representations, but musical education
does a better job of constantly reinforcing the relationships collectively than in the math
domain, where students can perform well in a given area, but ultimately will stymie their
progress if they can not relate it to a great number [and representational] sense. A more
comprehensive approach is needed to support the areas [seemingly separate - from a novice’s
perspective] of math education (such as number sense, functions [add, subtract, multiply,
divide], fractions, geometry, algebra, and beyond) to collectively reinforce the relationship(s)
between them. Previous work in the areas of math and music education (both individually and
The Sound of Fractions
18
collectively) attempt to address how to teach each subject simultaneously (in parallel and
mixed settings). The interesting approaches are how elements of musical education ( such as
novice-level practice strategies, notation/representations, and form/structure) might bridge the
gap between enabling students to climb and enabling teachers to pull students up (Acotto &
Andreatta, 2012; Courey, Balogh, Siker, & Paik, 2012; Graziano, Peterson, & Shaw, 1999; Upitis,
1993; Vaughn, 2000).
5.3 Math, Music, and in Between
Previous work encompasses evaluation and revision of academic instruction, musical
performances, and influential design strata. The problem of how to help children struggling
with fractions is addressed through developing the theoretical elements in teaching
approaches, revising the instructional framework, building better representational references,
and utilizing elements of musical theory that provide useful insight into mathematical theory.
Our aim is to present a culturally relevant, academically grounded, and design oriented
perspective to include student agency, both afforded and enacted, an overlooked component
of the learning process. We found that there is room for improvement in what representational
affordances we provide students, and that music can function both as a motivating feature and
framework for mathematical theory.
5.3.1 Revisiting Educational Approach to Mathematics
The following theories are the prominent attempts to revise how math should be taught
without incorporating elements of musical theory.
5.3.1.1 Rational Number Project (RNP)
The numerous and varied descriptions of the system of fractions emphasize the
difficulties some children experience in the learning process. Fractions encompass the five
basics of the Rational Number Project (RNP) (1976 - current):
1. relationships between the part(s) and the whole,
2. how to measure them,
3. ratios,
4. operations, and
5. quotients (Behr, Harel, Post, Lesh, & Grouws, 1992) based on the rational number
components from Kieren (Kieren, 1976).
Arguably, a student cannot even attempt the last three basics (ratios, operations, and
quotients) if he or she fails to understand the initial relationship between parts and wholes or
the language or mechanisms to quantify them.
5.3.1.2 The Splitting Loope
Research on the way that students come to understand the system of fractions has
progressed since the introduction of RNP. Major work was done by Lamon to show the
strongest component, or `subconstruct', is measurement, the second of the five basics of the
The Sound of Fractions
19
RNP (Lamon, 2007)(Lester, 2007). Two separate longitudinal projects investigated the cognitive
reasoning involved in the overall complete process as a part of ``The Fractions Project'' by
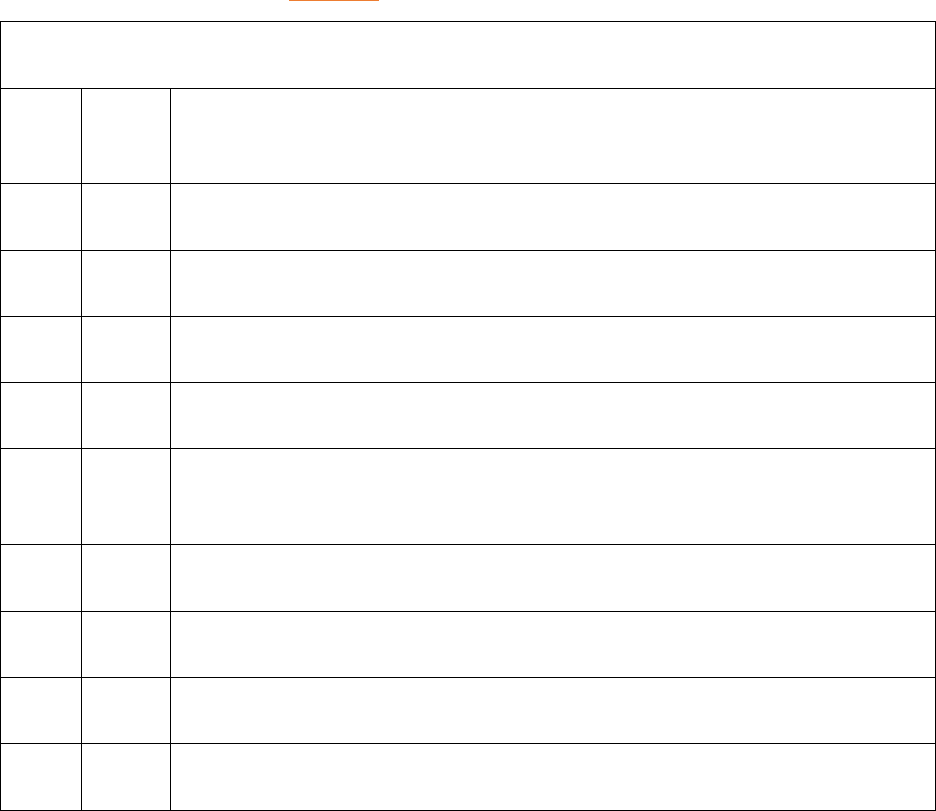
Steffe and Olive (1990 - 2002). These two studies deconstructed the many cognitive steps
employed by children (Gromko, 1994)(Anderson Norton & Wilkins, 2009). Building on these
works, Norton and Wilkins have collected and organized these cognitive steps into a more
cohesive and comprehensible structure of fraction schemes, referred to as ``The Splitting
Loope'' (Wilkins & Norton, 2011). Norton and Wilkins identify the following main schemes (A
Norton & Wilkins, 2013):
a) Part/Whole
b) Partitive Unit Fraction Scheme(PUFS)
c) EquiPartition Scheme (EPS)
d) Splitting
e) Advanced fraction schemes
The progression of these schemes can be viewed in Figure 5-2 (The Splitting Loope
schemes according to Norton and Wilkins (2013)).
Figure 5-2 The Splitting Loope schemes according to Norton and Wilkins (2013)
Part/Whole includes partitioning (separating the whole W into n parts), but does not
include iteration. Iteration plays an integral role in PUFS and EPS schemes. EPS is a scheme
that students use to partitioning a whole into `equal' pieces, and they iterate over ONE of the
pieces to verify that they are equal, comparing the whole against an iterated piece, not
comparing the pieces themselves. PUFS is a way that students partition a whole into pieces,
and identifies one of the pieces as a part of the whole, understanding the quantity outside of
the fractional language. To understand the difference of the closely related PUFS and EPS,
Steffe explains, ``The partitive unit fractional scheme differs from the equipartitioning scheme
in the explicit numerical one-to-many comparison (one-to-ten) and in the explicit use of
fractional language “one-tenth” to refer to that relation'' (Steffe, 2002). Splitting occurs by

The Sound of Fractions
20
students who can split iteratively, not recursively (Confrey, 1994) . That is, students split by
starting with a best guessed sized piece of a whole and do so iteratively of the remaining
`whole' until the `whole' is exhausted, NOT splitting the whole into pieces, and then splitting
those pieces into smaller pieces, the way a rolling pizza cutter slices pizza.
The five schemes are important but nuanced and can be confusing to non-mathematics
education experts. It should be noted that they all have in common both the concepts of part
and the whole. The method(s) that the students choose to perform or validate the relationship
speaks to how well they understand the system of fractions, but even a novice who fails to
move beyond the part/whole scheme is still aware that there are two distinct parts, the part
and the whole. We leverage this novice-level knowledge of the student to include in our
curriculum and accompanying technical implementation, SoF, to allow students to experience
the part [beats] and the whole [rhythm] at the same time.
5.3.1.3 Equal Sharing
On a separate research track, Susan B. Empson approached studying fraction learning
with first graders with exercises based on equal sharing (Empson, 1999). [Equal] sharing is a
skill that young children have experience and informal knowledge with (Davis & Pitkethly, 1990)
(Pothier & Sawada, 1983). Empson was also able to identify that the students could solve
problems using strategies that involved order, equivalence, addition, subtraction, and
multiplication (division, although it can be considered as the inverse of multiplication, was not
covered). The curriculum followed the progression of partitioning from easier situations (2
cookies among 4 people, 4 pizzas among 8 people), to larger numbers and non-halving (8/16
and 16/20), and then to more complex partitions (thirds, ninths, fifths, sevenths) (Empson,
1999). This greatly influences our curriculum for particular stages and what musical activities to
challenge the students with and in what order (see the section 8: Curriculum for a
comprehensive curriculum overview).
5.3.2 Musical Theory as an Analogy to Mathematical Theory
Musical theory and performance has a wealth of features that can be approached and
incorporated into mathematical learning. We however think it would be disadvantageous to
the math domain, music domain, and students if we try and align the two domains in parallel,
or to just include both in the other. To provide a solid curriculum, interface, and therefore
learning environment with the highest positive impact, we studied many components of the
musical education domain as it relates to music theory, including performance (creation,
listening, entrainment, and emotions), structure (notation, vocabulary, descriptions, and
composition) and educational approaches (how they are scaffolded, what they include, and
what they avoid).
We identified the major contributions of music theory as it pertains to math learning:
the natural embodied interactions when performing music,
the act of teaching how to perform the music prior to presenting vocabulary to students
and the vocabulary itself used to describe representations of music,
The Sound of Fractions
21
the transfer of cognitive, temporal, and physical components into a unified musical
domain
Previous work on the utility of musical theory or components of musical theory cover
both the benefits a synthesized teaching approach could create for struggling students and the
consequences such an approach would have on music education - namely the possibility that
flaws in math education may bleed into student's perception of music and act the part of a
parasite and not a symbiotic partner.
5.3.2.1 Useful Components of Musical Theory
Music was well integrated in to the earliest of our civilizations, hence there are many
varying ideas for the order in which students should come to learn how to perform music
themselves (ABELES, HOFFER, & KLOTMAN, 1994) likely to predate some of our citations. A
major concern for teachers today is not what to teach (tempo, tone, representations or names,
hearing or distinction, performance or practice, rote repetition or mimicking, etc.), but the
order in which to teach them. Joseph H. Naef, the student and later colleague of Johann
Heinrich Pestalozzi (1746-1827) who professed experience before introducing names and
symbols, advocated for `Sound before Sign', and outlined seven recommendations to music
teachers in ``Principles of the Pestalozzian System of Music'' at a meeting of the American
Institute of Instruction in 1830 (McPherson & Gabrielsson, 2002). The first notable of these
recommendations for our research is that students should learn more active activities such as
[hearing and performing] sounds before more passive activities such writing symbols [notes] or
names. The other is to teach incrementally, one concept at a time and practice separately,
before more difficult tasks of attending to multiple concepts simultaneously (McPherson &
Gabrielsson, 2002).
Two of the most popular approaches to musical education in the US adhere to these
recommendations for active before passive activity and incremental learning, the Suzuki and
Kodály methods. The Suzuki method, a pedagogy developed by Shin'ichi Suzuki, focuses on
education students at an early age with rote performance prior to introducing or learning note
[symbol] reading. This approach is grounded on the way children learn their native language,
surrounded by actors performing the language, and the child speaks [producing meaningful
sound or music] before learning to read (Landers, 1984). The Kodály method, originating from
Zoltán Kodály, incorporates hand gestures, solfège (voice/tonal) syllables (e.g. ``Do-Re-Mi-Fa-
So-La-Ti-Do”), and cultural-relevant approaches, often determined by the teacher him/herself
(Sinor, 1997).
Previous work uses both methods to determine that music experience prior to math
improves math learning and spatial-temporal skills, specifically tasks that require mental
rotation or multiple solution steps for two-/three-dimensional mental representations, ones
that lack physical models (Neufeld, 1986)(Weeden, 1972)(Vaughn, 2000). Lois Hetland's
research shows that music instruction which introduces notation yields higher spatial-temporal
skills, especially in younger (< 9 year olds) children (Hetland, 2000). However, given the
research in this field with the largest impact size does not decouple music education prior to or
concurrently with math instruction to understand their separate contributions (Graziano et al.,
The Sound of Fractions
22
1999), ``further research is required to test the possibility that concurrent but separate math
instruction using spatial-temporal methods improves math performance.'' (Vaughn, 2000).
In addition to Vaughn's hint towards future research, music education professor Bennett
Reimer offers a very import warning about linking musical education or experiences to
increased mathematical performance and other domains. Reimer vehemently believes that the
integrity of the music education should not be exploited purely for gains in other domains, as it
undermines the value to improve people's abilities to gain ``meaningful, gratifying musical
experiences.''(Reimer, 1999). An abstract representation of Reimer's teleological objection is
that the ends (gains in other non-music domains) shouldn't justify the means (violating the
integrity of musical education), because the unintended result is the depreciation of musical
experiences and degradation of music education. However, we argue that using music as one
motivating feature in a broader more culturally-relevant teaching approach for other
educational domains does not devalue musical education or an individual's enjoyment of music.
Such an approach would instead provide individuals with a more holistic perspective on the
aesthetics of human experience. In this sense, incorporating elements of musical theory in
mathematics is inclusive not exploitative.
5.3.2.2 Entrainment
One culturally evolved social activity is entrainment - the ability to perceive and
synchronize internal thoughts or external movement to an external third party sound. Mostly
considered unique to humans (Kirschner & Tomasello, 2009), entrainment allows for individuals
to perceive sound, including `noise' with no inherent rhythm, to be perceived as having a
rhythm. This ability to perceive rhythmic patterns as external musical performances begins in
the first year of infancy and develops to discern between grouping (perceiving boundaries
between other groups, or between subgroups), rhythm (discerning the temporal intervals or
separation of beats), and meter (an abstract hierarchy of beats, denoted by the strength of
beats) (Trehub & Hannon, 2006). Kirschner and Tomasello tested infant response time to
synchronous tasks in a social setting; their results showed that children at least 2.5 years old
were able to adjust their drumming tempo outside the range of their spontaneous motor
tempo. Furthermore, all children performed better at the synchronous tasks when performing
in a social environment as opposed to a physical drum machine or a sound playing from a
speaker (Kirschner & Tomasello, 2009).
The role of third party external noise in signal processing arguably demonstrates the
humans are be able to process non-aural signals and perceive them as having meaning,
substance, and musical properties. Examples of this are the usefulness of visual metronomes as
an alternative channel to communicate a prescribed rhythm (Jordà, Geiger, Alonso, &
Kaltenbrunner, 2007), and haptic limb bands used for performance stimulation, coordination,
and feedback of polyphonic rhythms to train novice drummers using multiple limbs without
sounds that conflict to the drummers' own learning performance (Holland, Bouwer, Dalgelish, &
Hurtig, 2010).
The Sound of Fractions
23
Importantly, we, the authors, see entrainment as differing from coordination in that
entrainment is the ability to perceive and enact upon external sound or noise without
motivation or effort to change the tempo, meter, or grouping of the sound source, whereas
coordination involves the nuanced micro-coordination communication characteristics required
to adjust the individual and the source of the sound to produce an isochronous rhythmic
performance.
5.3.2.3 Embodied Interactions
Musical performance is inherently embodied, as is entrainment. Entrainment,
synchrony, and rhythm play an important role in embodied interactions, especially in
communication that is mediated (Gill, 2012). Paul Dourish reminds us that `embodied
phenomena are ones we encounter directly rather than abstractly' (Dourish, 2004) and occur in
real time and real space. Polanyi also provides that tacit experiences have two properties,
proximal and distal, together which enable a deeper sense of knowledge that are harder to
communicate explicitly XXX citation needed XXX. By focusing our curriculum design on tasks
that share these qualities we hope to create a learning environment that welcomes physically
expressive ideas and inquires for traditional represetations.
5.3.2.4 Expectation
Bobby McFerrin, a vocal virtuoso, gave a presentation to the World Science Festival in
2009 under the topic of ``Notes & Neurons: In Search of a Common Chorus'' and presented the
idea of expectations in a musical context. He began by standing in one location on the front of
the stage, facing the audience, and singing a medium pitched note in sync with jumping in spot,
and signaled with his left hand pointed to the audience to mimic in real time. After he felt that
the audience was performing in sufficient synchrony (after about 5 hops and accompanying
notes), he signaled with his left hand to the left [to the audience's right], then he moved to that
spot (to his left) and began singing a note of one step higher pitch. The majority of the
audience automatically followed with the higher note, while the remaining caught up on the
next beat. After jumping in the second higher position for a few times, McFerrin pointed back
to the first spot and jumps back, and adjusted his tone to the lower original tone, and the
audience followed in suit with no delay or mix up. He then proceeded to jump back and forth,
with no notification given before jumping between the notes, and the audience followed along
perfectly. His tempo increased quite rapidly, and the audience kept up. Then, still with no
notice, he jumped from the higher note [right-most position from the audience's perspective]
to an even higher note [farther position to the audience's right], but made no sound into the
microphone himself. The audience not only didn't miss a beat in timing, they also flawlessly
increased their pitch by one note's frequency of the same increase between the previous two
notes.
The audience's performance follows musical expectations according to McFerrin, and
occurs universally because of the [pervasively pleasing] pentatonic scale (a scale with 5 notes,
instead of the other traditional heptatonic scale, comprised of 7 notes) (McFerrin, n.d.). We
seek to align mathematical scaffolding progressions in the curriculum with natural musical
expectations to strengthen the understanding of the part/whole relationship. The idea of
The Sound of Fractions
24
universal expectations of what is stronger when a rhythm is present, as followers are able to
mimic the leader more with gestures as simple as hand movement (p<0.001), and also head
movement (Selecta, n.d.).
5.3.3 Elements of Educational Approach
The following elements of teaching music and math are focused on in previous work as
key points to creating a better teaching approach.
5.3.3.1 Scaffolding
Scaffolding is an important feature in educational curriculum, that helps balance
educational goals with student performance and expectations. This concept is especially
needed in scenarios that involve multiple students. Classroom activities often involve planned
group tasks. Tasks scaffolding should include:
1. the initial setup/condition of the activity [environment],
2. information about the activity, and
3. what tools [stimuli] are available to the students during the task.
To better understand the cognitive processes, it is also suggested that the instructor be
prepared for possible responses. Teachers should also be aware and have a mental model for
the different cognitive states of individual students between responses from the students
collectively (Newman, Griffin, & Cole, 1989). Michael Cole clarifies that the task is not
necessarily limited to the exact initial communicated assignment, but rather its interpretation is
co-developed among students during the execution of task in practice, and their task emerges
as an ``interpersonal, public resource for coordinated action'' (Cole, 1998). Understanding the
stages of scaffolding of the curriculum, cognitive stages and process of the children, and that
the meaning of a task from the students' perspective changes during the task is integral in
developing a robust curriculum and technologically mediated tool to present to students to
help improve their comprehension in any domain they are struggling with. The task of
developing a robust system is even more difficult when mixing domains (Reimer, 1999), but
also strengthens the need for paying attention to the nuances of the cognitive stages and
potential miscommunication that come along with making analogies.
5.3.3.2 Engagement
Engagement is another important factor in educating students, especially children. Our
original motivation for this research, from the initial prototype, is that the students were highly
engaged in discussion, and motivated to follow teacher prescribed classroom rules to help
facilitate learning that were previously ignored.
5.3.3.3 Proximity
Musical performances most often occur with all musicians co-located and in relative
immediate proximity. With more recent advances of electronic technology and the music
industry itself, the musical community now features musicians that are separated from one
The Sound of Fractions
25
another, separated from the audience, and separated from the instrument. Close proximity
allows for robust nonverbal communication on channels to be fully utilized between musicians.
Mustafa Radha categorizes the channels into three main groups: (1) Visual, (2) Verbal,
and (3) Auditory (Radha, 2012) and Robert Beaton supports this in his research of what leaders
perform during music making performances (Beaton, Harrison, & Tatar, 2010). Visual channels
include eye contact, breathing, head nods, facial expressions, arm movement, and body
movement (Selecta, n.d.). Verbal channels include words, breathing, sounds produced by the
mouth, or tapping. Auditory channels include loudness, pitch, rhythm, tapping (of a foot or
hand), snapping, non traditional musical performances (e.g. an extra tap of the cymbal, a non
tonal breath pushed through a wind instrument, a hammer-on of a stringed instrument, etc.).
Some actions can be communicated over more than one channel such as tapping, as it has a
visual performance, an verbal direction, and auditory rhythm.
Beaton explains that future work in remote proximity may have important insight into
the role of leadership and collaborative coordination performances (Beaton et al., 2010). There
are even more considerations for communication channels between musicians as a group and
the audience as a group that are not discussed in this paper.
5.3.3.4 Synchronous Coordination
Drumming performances can grow to become quite complex, starting with easier
patterns such as simple meter (each beat has two equal parts), and growing more difficult with
compound meter (each beat is divided equally into three parts), mixed meter (a.k.a. additive
rhythms: adding different rhythms played in a cycle [group]), to quite challenging polyrhythms
(a.k.a. cross rhythms: using two or more rhythms simultaneously). There is also metric
modulation (where the drummer switches or segues between rhythms at intervals matching
the grouping), polymeter (involving two separate beats played simultaneously, the beats and
tempo being equal, but the measure size differing [the meter {strength of the first beat in a
measure} being different]), or the meta-metric hypermeter (the measures themselves act as
individual beats)(Neal, 2000). All of these rhythm patterns require copious amounts of
attention to muscle movement and memory, external stimuli, and other performers altogether;
they are all forms of coordination.
5.3.3.5 Communication
While our newest implementation shares many characteristics with the growing trend
of collaborative tabletop music interfaces, it may or may not fully fit the classification (Blaine &
Perkis, 2000). Having a single electronic interface for several people to interact with forces
students to discuss what actions are taken, before or after they are enacted. This keeps the
conversation going, as students rearrange the representations to elicit particular phenomena
for discussion. It does however pose problems for classroom management and personal
agency. With individual computers, students are able to make choices on their own. With an
accompanying curriculum, their actions and thoughts can be guided to focus on particular
fractional properties that wills scaffold towards a stronger understanding of the system of
fractions. Individual devices also allow participants to focus on the communication required to
The Sound of Fractions
26
complete the activity and understand the takeaway message. This differs from coordination in
that they may be able to perform the musical component of the exercises, but will be
challenged to communicate the reasoning behind their performance choices, hopefully in more
mathematical descriptions as activities progress.
5.3.3.6 Micro-coordination
Understanding the taxonomy of micro-coordination interactions allows us to
understand the different coordination interactions are being done, design for them, and have
the design be meaningful in the communication between musicians (Radha, 2012). Some tasks
that musicians perform while making music are synchronization of tempo, rhythm, harmony, or
a more complex complementary synchronization, where the musicians collectively produce a
continuous sound, but alternate (with or without a pattern) making sound individually. This
form of fast paced non verbal communication and synchronization can come from repetitive
practicing, sometimes found in drumming circles, and can include a mixture of novices and
experts (Beaton et al., 2010). In more formal settings of music making, notations of shared
resources help clarify goals, mood, and musical direction for reference when playing the
musical piece through at a later time, helping memorialize all of the feelings in an easily
consumable form.
5.3.4 Building Better Representational References
Literacy, dscribed as the ability to Read and Rite (and colloquially perform Rithmetic to
achieve the three R’s) is pinned/under by the ability too comprehend and compose ideas in
waze that are meaningful, so that it may be communicated (back two one’s self or too others).
While the previous sentence is both lacking in vocabulary and grammatical correctness, if read
aloud, it should be interpreted correctly given the power of homonyms, slurring of words, and
other literary devices. This is the strongest tenant and motivation for of our work. While one
representation can be confusing, another can exemplify the focal meaning and ideas easily. A
call to use the three C’s (comprehension, composition (Grainger, n.d.), and communication) is
more appropriate. Using the CCC’s are how teachers [and other knowledge holders] can
ascertain what students [and peers] actually mean. This shift of focus from Rs to Cs (like a
pirate’s favorite letter, thought to be the Rrrrr, when their true love is the Ceeeea) is an
important step in educating the students who are already behind, as it returns their own
agency for them to create and compose, contextualize, compare, and communicate their
comprehension from a domain they are already excited and familiar with.
Empson’s a posteriori approach to mathematics mitigates the cognitive steps of solving
math problems with meaningful personal experiences. This meeting between mathematical
concepts and real-world implications introduces the third approach to helping struggling
students with fractions - representational references.
With students being forced to repeat the same curriculum after unsuccessfully
comprehending the previous year or semester, the curriculum loses its power of novelty. As
students continually are exposed to the same representations and information about the
concepts and characteristics, the features become more difficult to discern and appreciate.

The Sound of Fractions
27
This motivates us to include new and novel representations in SoF. Well designed two-
dimensional objects can be very expressive of multidimensional musical concepts for music
making interfaces (Patten, Recht, & Ishii, 2002). Jorda et al. make progress with
representations by mapping geometrical shapes to particular musical sounds, filters, or features
such as a circle as a metronome or a decagon (geometrical shape with 10 equal length sided
and 10 equal angles) for a decimator (a noise reducer) (Jordà et al., 2007).
5.3.4.1 Culture & Ethnomathematics
One strategy of successful math teachers is to adapt their approaches to students at an
individual level, interacting one-on-one with a student to address specific needs. Teacher
perception of one-on-one educational approaches directly affects their instructional
interactions and mechanisms used in inclusive learning environments (Jordan, Lindsay, &
Stanovich, 1997). A key concept to consider and give weight to is ethnomathematics, the
relationships between culture and mathematics (D’Ambrosio, 2001). The compound word
``ethnomathematics'' can be deconstructed to the terms ethno describing ``all of the the
ingredients that make up the cultural identity of a group [or individual]: language, codes,
values, jargon, beliefs, food and dress, habits, and physical traits'', and mathematics expressing
a ``broad view of mathematics which includes ciphering, arithmetic, classifying, ordering,
inferring, and modeling'' representations (D’Ambrosio, 1987). Teachers who embrace
ethnomathematic approaches with students enable teachers to address student needs through
leveraging students' past personal experiences, rich cultural past, and introducing cultures that
are foreign to the individual student or the class altogether. Ethnomathematic approaches help
create periods of empathic immersion for students to help understand math from the context
of their own culture, reaffirm their understanding of their culture, and experience opportunities
to explore other unfamiliar cultures. Therefore, teachers and students can use a wider range of
cultural artifacts (or references) in their exploration of new academic material, as well as
traditional curriculum material to compare or contrast against.
5.3.4.2 Cross-domain teaching
Fractions are already taught alongside other educational areas (Courey et al.,
2012)(Winner, 2007). Some common domains that have been used to teach fractions are food,
music, dance, visual arts, and photography. Each of these approaches uses a particular domain
to appeal to the students, and is described further in 5.4 Other Cross-Domain Approaches.
5.3.5 The Role of Technology in Mathematics Learning
Technology to help teach mathematics in the classroom is approaching its 50
th
year
(Kaput & Thompson, 1994), and has proven to be of great help. Technology also has had
negative effects(Fey, 1989). Researchers, academics, and professionals have been trying to
identify and add beneficial technology while avoiding the negative attributes ever since.
Technology in the mathematics learning domain:
Reinforces the pedagogical shift towards active learning (Kaput & Thompson, 1994)

The Sound of Fractions
28
Aids in graphical representation of complex or abstract modeling (Fey, 1989)
Creates external symbolic and cognitive representations (Shaffer & Kaput, 1998)
Allows rapid deployment and trials
Provides reusable, distributable, configurable, and potentially personalizable resources
Has the potential to reduce costs associated with education
Our research follows in this tradition by approaching from a socio-technical approach,
guided by our own curriculum, and engaging in a domain appealing to students.
5.4 Other Cross-Domain Approaches
Given the barrier to understanding fractions exists for many students, it is not surprising that
many educators, academics, parents, and administrators look to alternative ways of teaching
the subject and associated concepts in and outside of the classroom. While these examples do
highlight other domains, they lack as robust of an approach as we do with an aligned
curriculum.
5.4.1 Music
XXX
5.4.2 Food
XXX Hot dog item. Matches the physical building block manipulatives
5.4.3 Dance
Dance is used to teach mathematics, with attention to agency given to the performer in
actions or steps that can be described with fractional qualities. (Cummins, 2009)
5.4.4 Embodied
Action, touch, and other embodied interactions support cognitive learning in multiple
domains, especially math (Segal, 2011). One example is where students use hand movements
to mark and generalize relationships between parts and the whole with visual feedback
(Howison, Trninic, Reinholz, & Abrahamson, 2011).
6 OUR PRIOR WORK
This thesis document is a culmination of many intentional works, ideas, experiments,
and the byproducts of larger related grants and funded by many smaller grants and institutions.
To understand how we came to the most recent study ( as described in 7 The MAIN Study ), it is
best to look at the work we did that led us to our main study.
The Sound of Fractions
29
6.1 Proto Computational Thinking
We, the authors, worked with teachers in a study to help incorporate computational
thinking in the classrooms of a low socioeconomic status (SES) middle school in the US.
Circumstances were such that a school program provided every access to a laptop for the
school day and to take home. The students we worked with, aged 11 to 13 years old, were in
6th grade of a middle school in the northern region of Virginia, United States (US), who are
guided by the Virginia SOL, not the CC. The majority of the students in the class and in the
school as a whole were of a low SES, and participated in free or reduced lunch programs. This
school was in particular of interest because of the administrative program providing one laptop
per child; each laptop was fairly new, with a large color screen, several gigabytes of RAM,
powerful processor, and modern web browsers (Google Chrome and Mozilla Firefox). This
enabled computer exposure on a daily basis at school as well as at home, with a deposit of
under $50 USD, mainly required for asset tracking purposes.
We were working with a NSF grant to study how to include components of
computational thinking into the classroom from each of major education domains (math,
science, language arts, history, etc..) to help seed the future potential for understanding
computational thinking. Computational thinking, a term coined by Jeannette Wing, describes
the properties of thinking, problem solving, and structures that are fundamental to computer
science, and can be extended and applied in all domains (Wing, 2006). We believe that
teaching computational thinking begins without the use of computers, especially in the context
of computer science, and should be approached concurrently alongside the other major
education domains.
The math teacher we collaborated with noted to us that fractions were a major hurdle
for his students. Many of his students had failed the same class for one or more years prior to
the current year and showed continuous lack of engagement for traditional curriculum. Over
the course of the observational phase, we observed disengaged students not participating in
classroom discussion of the math curriculum but rather were tapping on their desks with their
fingers and pencils, effectively drumming to pass the time. We then identified that numerous
students in the class were also enrolled in music classes, predominately band, and even
participate in extra musical performances such as marching and jazz band. This discovery was
our motivation to explore the area of music and fractions in the same setting; our conception of
this area influenced the design phase for our initial prototype. When we introduced our
prototype, a rudimentary beat-box machine that automatically calculated fractions of the ratio
of beats to a measure. Student and teacher interest soared, despite the lack of strong
accompanying curriculum. To address the issues surrounding the lack of mathematically
grounded curriculum and maintaining student engagement, the existing body of literature on
these topics must be reviewed.
6.1.1 Proof of Concept
To test the viability of teaching fractions to students with a new approach of using their
musical prowess, we developed an interactive web application for the teacher to use as an
The Sound of Fractions
30
accessory in the classroom. Students were mostly African-American and of a low SES, and
were provided free or reduced school lunches. The students also were several years behind in
the state’s learning standards that have similar progressions at the country wide level of the CC.
The prototype we created was purely interactive with the mouse. It provided
functionality for students to
• See the relationship between the beats [parts] and the whole [measures]
• See multiple representations of this representation: several mathematical (proper
fractions, improper fractions, mixed numbers, decimals, and percentages), one aural
(the sound), and one graphical (bars)
• Create their own music by adjusting the number of beats in the measure (this is
equal to the PUFS fractional scheme)
• And operate in a novel and different classroom environment than they are used to
6.2 Redesign and Conjectures
After making an initial proof of concept that had different goals and intentions, we
noticed several issues when testing with students, mostly surrounding the lack of any
curriculum, let alone one that corresponds to the interface or goals of teaching fractions. With
new insights for consideration, we sought out to redesign a new approach from the ground up.
6.2.1 Agency
When teachers are forced to meet criteria that doesn't account for or adapt to the
needs of a large group of students, then it actually marginalizes students and sets teachers up
for failure. Pasi Sahlberg, a scholar and expert on Finnish education, attacks the Common Core
as an experiment on children and has said many times that `accountability is what is left when
responsibility is taken away from teachers' including the 2014 National Superintendents Forum
(Salsberg, 2014). These guidelines have turned into requirements that in turn restrict learning,
not expand. This has a devastating effect on the students we are educating, as they have been
stripped of their agency in the environment that has been created for them. We seek to open
up the learning environment and give the students affordances to exercise their agency.
6.2.2 Design
We focus the redesign on two main non-mutually-exclusive perspectives, the individual
student, and group tasks. Taking these into consideration, the design manifests itself in both
the curriculum, the web program (its user interface (UI), and user experience (UX)), and guiding
the classroom interactions.
6.2.2.1 For The Individual
Allowing the students to create on their own returns some agency to them. Not all
activities can be an open play area for creativity, as some tasks will need to be designed to bring
forward a particular mathematical or musical phenomena, but bearing this in mind during our
The Sound of Fractions
31
design process will allow many of the tasks to start with rhythms and representations created
by the individual students themselves.
6.2.2.2 With The Group
With groups that have shared goals or tasks, leaders will emerge, and others will follow
(Rands, Cowlishaw, Pettifor, Rowcliffe, & Johnstone, 2003). It is important for the students
interpersonal, social, and personal skills to be in small leadership roles. It is equally important
to be in a non leadership role, to hear other's thoughts, experience empathy, and have time to
reflect. These experiences in different roles will also help their negotiation skills, as we will not
dictate who goes in what role first.
Tasks that are designed to be done individually, as a group, and as a class allow the the students
to become socially aware of their peers, environment, and context; students also can reflect on
their position in situ respective of their social arena. Working in groups also allows for the
chance to imitate one another to enhance their skills and understanding of music and math.
The students will be faced with questions and challenges from their peers that they must
defend or change their own concepts and approaches to account for alternative viewpoints.
Teacher oversight will help guide the students towards the important phenomena that is at the
heart of the task, as well as avoid the negative situations such as constant public failure,
ridicule, distraction, frustration, and disengagement.
These highly complex multi-channeled communication networks are accessible to students
given their social and academic experiences. This level of robust communication can not occur
in distal and remote situations. As the distance increases, more technologically mediated
solutions must come into play, and although some implementations are able to increase clarity
and affordances for particular communication features, they come at a cost of impeding other
channels. This exchange and loss of communication and instruction is not acceptable for
students that are already in a foreign learning environment, and trying to focus on
mathematical phenomena, as they don't have the expertise of high fidelity remote interactions,
and we as educators likely can not provide them either.
6.2.3 Brainstorming Sessions
We brainstormed for several sessions around the key components of fraction learning,
embodied interactions, and entrainment with experts in design, curriculum, education, micro-
worlds, and technology. The main ideas that came out of our brainstorming sessions that
showed the most potential surrounded layout and representations which led to a scaffolded
curriculum balancing off-computer interactions and slowly increasing computer usage.
6.2.3.1 Representations
The idea of providing multiple representations stems both from an abundance of
traditional mathematical representations in current standard curricula and from the previous
version that had buttons for allowing each instrument’s corresponding fraction to be
represented in different forms ([improper]/fractions {5/3}, MIXED num/bers {1 2/3},
percentage% {166%} and de.cimal {1.66}). Upon further review, having the system auto-
The Sound of Fractions
32
calculate the fractions of beats that are on our of the total number of beats available has many
problems. When the computer completes these ‘simple’ tasks for the students, the students
have less agency, are not challenged to identify what truly is important about the
representation at hand, are distracted from thinking beyond the provided calculation, are
reinforced that fractions ‘are’ easy and not ‘can be’ easy, and are limited XXXX.
We brainstormed several designs that were based on steam rollers (rolling out copies of
the same representation), a rosary bead, necklaces, paint[brushes], and other creation
mechanisms. Once we had several different representations that we often card sorted to make
sense of the mathematical properties we wanted to highlight, we began to focus on the
interaction design, and it became obvious that we would also have to be aware of and
potentially account for manipulating the representations’ size, shape, colors, and perspectives.
We designed five graphical representations and three audio representations to interact
with. The graphical representations include the Audio, Bead, Line, Pie, and Bar. The audio
representations include the Snare, High-Hat, and Kick Drum. With these multiple
representations in both graphical and aural domains, the student’s will be provided multiple
ways to see, hear, feel, manipulate, experience, interact with, and study the fractional
properties.
The Audio representation is a default view provided with all representations, although it
may be removed if the student chooses to. It is the first way that we provide a mechanism of
representing something that is tapped, heard, internally discerned, or experienced.
The Bead, Line, Pie, and Bar are the remaining graphical representations, and we refer
to them as the Core Four. We plan on working with these representations the most, with each
representation having strengths that are unique, and some sharing certain properties that will
be highlighted during certain exercises.
The Bead representation is our strongest novel contribution, with several properties
that enhance the learning experience for fractions. Its circular fashion helps reiterate the idea
of repetition. Its beads with appropriate separation highlight the distinct separation between
the parts. Its resemblance to a necklace provides a great transformation into a linear form.
The Line representation is another contribution by our team, as it is subtly different
than typical number line representations presented to students. The Line is purposefully not
labeled between two numbers (whole or otherwise), as fractions can exist between any two
referents. Additionally, we provide a labeling mechanism for students.
The Pie representation, a very common form of presenting fraction problems, is
presented in the same form that students have already been exposed to previously.
The Bar representation is also a standard representation that students have been
exposed to. For this reason, both the Pie and the Bar representations are presented last as
options to represent their rhythms. They still have importance, as it will allow them to visualize

The Sound of Fractions
33
their rhythm creations in a standard representation, as well as have a reference when working
with multiple representations simultaneously or in stepped progression.
All graphical representations will graphically and aurally distinguish between beats that
are turned off (non-sounding) and beats that are on (sounding). They also will auto-space, and
properly reflect equal unit fractions. Undoubtedly students will want to move beats closer
together (with less space between them) to make them appear faster, but we discourage this
so that the students can understand the other related parts (the division of the whole and the
other beats [rests] that need to be considered) when rearranging unit fraction based rhythms,
the primary structure of our application for study. All graphical components/representations
(accompanied by a corresponding aural representation [with each set of graphical
representations grouped by instrument type/sound]) represents each of the underlying beat
patterns of the matching rhythm being interacted with.
The Core Four will provide mechanisms to stretch (to lengthen the duration – sounding
as if to slow down) or shrink (to shorten the duration – sounding as if it speeds up) the
representation. Instances can transition between each other ( discussed in 6.2.4.3 Transitions ),
be added (multiple times even to show consistency and abstraction) or removed, and
rearranged. Each of the Core Four individual representations will also have the functionality to
transition between them to show what is conserved, what is lost, and hopefully highlighting
what is important when analyzing representations in a fraction or mathematical context.
Additional information can be found in 9.3 User Interface (UI) )
6.2.3.2 Layout
Dealing with multiple representations brought about a problem of screen real estate,
and what to include and what not. While zensign (the conscious effort and decision of what not
to include) XXXCitation neededXXX is just as important of what to include to help the students
learn, the layout goes beyond graphical elements. Given the target student audience and their
current limitations and the entire learning environment that the students are being subjected
to, we need to consider how these all weigh on each other and in relation to and our goals of
incorporating music, motion, and agency.
To help choose what should be included in the electronic interface and what should be
presented over other channels, we devised some basic math questions, potential labeling
mechanisms, physical material design based prototypes, and representations (as described
above in 6.2.3.1 Representations ) to separate the large amount of information that is
presented to be scaffolded, limited, direct, cohesive, and meaningful. Using a material design
approach, we cut out scaled medium fidelity paper representations to be rearranged
representing the digital screen dimensions. This allowed rapid prototyping of additional
representations, and to study the intended interactions in conjunction with the curriculum,
which would include off-computer activities.
When including computers and other digital tools into the environment where students
would be learning, we know that it is important to include the complications that go along with
such electronic devices. For our study, these complications of course include power

The Sound of Fractions
34
requirements, internet usage, logging of data, cable layout, setup and distribution, a novel
learning tool and the potential for a distraction, and other numerous complications associated
with electronic devices. It is also important to consider the implications of incorporating devices
that are meant to help communicated between people. Emotions can be negatively impacted
using computers, while discussing highly complex or novel perspectives also are a factor (Lee &
Tatar, 2014; Tatar, Lee, & Alaloula, 2008).
6.2.4 User Interface (UI) Components
After several brainstorming sessions (described in further detail in 6.2.3 Brainstorming
Sessions guided by the principles discussed in 6.2.2 Design ), several major UI components
came out of our new design: instruments, labels, and representations. There are also other
minimal UI components to help manage electronic interfaces, such as logging in, a reset button,
the name heading, and light demarcations to help the user separate components.
6.2.4.1 Instruments
The students can select from among three instruments: Snare, High Hat, Kick Drum. All
interactions start with a Snare, that they can remove and add a different instrument. We
provide three to allow the students to have options, to take up screen real estate, and to use
the multiple instruments for deeper investigation into fraction learning. Some activities allow
for comparison between two representations within the same instrument [rhythm]. Others
allow students to compare representations with different underlying rhythms. A few activities
utilize the third instrument to make hypotheses and adjustments to their hypotheses without
affecting the other two instruments, or as a reference representation to reach as a goal.
6.2.4.2 Labels
Labeling allows the students to begin to interact with their mental models of the part
and the whole and try and concretize it in a way that is both meaningful and mathematically
accurate. The ability to change their labels is also important, as they begin to interact with or
gravitate towards particular ways of labeling rhythms, it may not apply to rhythms with
different patterns, sizes, or representations.
Providing prefilled labels would cost too much screen real estate, we would need to
account for whole numbers 0-16, as well as every unit fraction and fraction for every possible
rhythm, up to 16 beats, and also possibly decimals and percentages. This approach also does
not allow the students to fail, for example if we provide only relevant fractions for a rhythm
with three beats, the student would not have an option to label with a 4, when there may be an
argument for that, especially if the student has a misconception about the system of fractions.
To provide the best balance of options and interaction, we provide the vinculum (the bar
between the numerator and the denominator in a fraction) and whole numbers 0-9, in that
order. This allows students to label things as whole, order, odd, even, and more just using the
whole numbers. It also allows them to construct their own fractions to count beats relative to
the rhythm, beats with regards to their state (on/off), improper fractions, or other non-
traditional labels and descriptions.

The Sound of Fractions
35
6.2.4.3 Transitions
To help students strengthen their knowledge about fractions and that fractions are
abstract representations of real world things, we want to highlight what is conserved between
representations that have the same underlying structure (i.e. 3/5 or 6/7) of relationships
between the parts and the whole. We attempt to accomplish this through synchronous
animations of the various components that portray our representations ( as described in Error!
eference source not found. Error! Reference source not found. ).
We support full transitions between each of the Core Four. We do not support
transitioning between the Audio and the Core Four. The Audio representation provides a
strong mechanism to communicate to the user that the microphone picked up a beat when
recording, and also when any beat is making a sound, however, beyond that, we allow each
individual to internalize the music as they experience it. Each transition between the Core Four
has distinct stages to help the user see what is going is being transitioned, what is being
removed, and what is being added.
6.2.4.4 Technology
The students have access to a technologically current laptop, and we also supply
additional units. Planning for wide-spread deployment, we developed a web application to
avoid varying technology and IT related barriers at different schools and instruction locations
and avoid purchasing a standard computer that may age faster than the technical development
of the web application. We only have to develop for a particular web browser version and can
avoid different operating systems as time progresses. Given multiple study locations and the
potential for students to engage with SoF outside of school, especially in rural areas, we
account for students having intermittent Internet access at the house by allowing the web page
to be run in the `off-line' mode as well as capturing their data while they are disconnected and
it uploads once reconnected.
6.3 Iterative Redesigns
We used our major redesign in several smaller usability studies that were often
conducted during community exposure events and seeking potential study participants. Ages
ranged from 5 to 14 years old, and targeted activities typically lasted five to 30 minutes. During
these miniature studies were identified several things.
Despite a relatively wide range of age groups, some common themes were observed
with a strong presence :
Discussing fractions in terms of rhythm is initially difficult, but becomes easier
Describing rhythms using math terms is easier than describing math terms in terms of
rhythms
The children have difficulty with accurate mouse movement
The children become confused and sometimes disengaged when presented with the
technological environment with no goal or priming activity
The Sound of Fractions
36
The children need stateful feedback of the technology when performing multi stage
interactions
Having colors is more attractive than no colors
Animation coupled with sound is attractive
6.4 Moving towards future opportunities
Using the information gathered from the small studies, we:
adjusted the interface with larger buttons and accompanied text descriptions
added messages that help students when adding or transitioning a representation
used a consistent color scheme
Adjusted the curriculum to better scaffold the progression of topics, with each activity
helping prime the next
These enhancements are very beneficial, however there are other hurdles that arose
and needed to be addressed. Our prior works were primarily based in an urban setting with
support from teachers, school level and district level administrators, and funded through
national grants. This strong support network came to an abrupt end when a key leader in the
team passed away suddenly. This greatly hindered future progress in that particular setting in
which so much of our work had been grounded. We no longer had access to students in an
urban setting, or with access to a ‘one laptop per child’ program. This required a great shift in
the recruitment for future prospects.
Our academic institution, Virginia Tech, is located in Blacksburg, Virginia, US, considered
a relatively rural area despite the large university’s presence. Our recruitment efforts to
contact relatively close participants was met with many additional hurdles. The immediate
community has many protections for children given the numerous research projects that are to
be administered given the proximity to the research goals of the university and its affiliates.
The level of paperwork and other administrative hurdles alone made it difficult, not including
the typical requirement to have initial promising data, something that we could not solidly
provide. Considering after school programs, private and charter schools, and other extra
curricular communities also proved challenging to our research efforts. Many of the population
around the university is of a median or higher SES, and thusly, the students typically are
excelling in math and other subjects in and out of school. This eliminates the focus group, as
students who already understand the system of fractions do not fit our target audience, and
have less of a reason to entertain alternative approaches for learning ‘old’ material.
With these limitations, we sought to expand our community to include rural low SES
communities, and not restrict to urban settings. Through a university outreach program, we
were able to establish promising connections with a community 2 hours away. This community
is quite rural with generally low SES members. This opportunity was pursued to approach our

The Sound of Fractions
37
research interests, even thought the goals and approaches had to be adapted to meat the
needs and challenges of the newer community.
7 THE MAIN STUDY
After several smaller individual sessions, we were poised to use the data collected to
fully develop a longer study lasting several sessions. To make a meaningful educational tool
and learning environment, we needed to work on developing a solid curriculum, address the
technology and its hurdles identified in the earlier studies, and find students who both need the
help and were able to work with us.
7.1 Motivation and Goals
Our areas of interest for this study are:
Providing a study that provides positive learning impacts for students to learn fractions
Have students experiencing the part(s) [beat(s)] and the whole [rhythm] at the same
time
Study the compelling, embodied, culturally-relevant activity of drumming and making
rhythms
Study how performing rhythms allow students to experience the wholes, the parts, and
the relationships between them at the same time
Provide and study the inclusion of a new computer-based representational
infrastructure
Introduce a new representational infrastructure comprised of aural, visual, physical, and
temporal components
Provide a curriculum that scaffolds classroom-based activities that bridge the
relationship between percussion-related and mathematics activities
Have students be able to create, identify, and manipulate [gradually] more standard
mathematical representations and usages
Provide multiple open and accessible data sources for analysis by students, parents,
administration, and academics alike
Leave students with skills that extend beyond our study what enable critical and
computational thinking with representations and other abstract ideas on multiple
domains
7.2 Curriculum
We developed the curriculum so that students can involve themselves in a creation,
identification, and manipulation environment. This approach allows for inspiration and
exploration by the students themselves. To market our study to potential schools and
administrators, we also looked at accommodating flexible sized groups, different locations, and
varying class and study durations. To accommodate a wider potential audience, we also
reviewed the requirements for students to simultaneously be in a music class, and expanded

The Sound of Fractions
38
our control group to include all students who struggle with fractions, as music interest was still
strong within this population, and only including those who are musically talented may be too
restrictive. We instead approached the activities from a more inclusive approach, and kept
drumming activities approachable and interesting for all skill levels. See 8 Curriculum for a
detailed description of the development of the curriculum and 15.3 Blank Lesson Plan and 15.4
Curriculum for the actual curriculum.
7.3 Programming and UI
To be able to run our study with the accompanying curriculum, the technology needed
to be designed to fulfill many of the goals we were focusing on. First and foremost, we seek to
provide an educational tool that has positive effect for students and their community. To
accomplish this, we have to consider, the curriculum as an accompanying tool, the embodied
nature of rhythm making, classroom management and layout, and the technological restraints
of school systems. The user interface also must be considered as how it plays into the user
experience as a whole with all of our goals. See 9 Programming and UI for a complete
description of the development of the technology.
7.4 Prospective Students
Through a community connection with a local nearby county, we began working with a
school and a church who both host afterschool programs. Both face the same challenges with
rural, low SES struggling students and communities. More detailed information about the two
groups is provided in 10.1 Demographic Information.
8 CURRICULUM
Our first implementation to aid fraction learning for middle schoolers with drumming
from a computational thinking perspective shined light on a very important area for
improvement, the accompanying curriculum. With a better understanding of the previous
research conducted ( see 5 Literature Review ) and several targeted design sessions ( see 6 Our
Prior Work ), we aimed at addressing the educational needs of the students while considering
the culturally and socially relevant perspectives they own.
8.1 Education Requirements
Quality education has many qualities. To begin to approach teachers, administrators,
and school systems, we needed to consider the external requirements imposed on these roles
in addition to the goals that each has. Many of the people in these roles share the same
overarching goals, but how they interact, participate, and execute separates them from the
large swaths of overarching goals. In order to communicate to each person what work we have
done, we studied the different standards proposed by the states that we were pursuing to run
the studies in, as well as a common national standard and cross referenced each of them to
identify which areas of learning we were targeting that aligned with the current educational

The Sound of Fractions
39
structures. We pursued schools, after school programs, and community programs in the state
of Virginia (southern United States [US]) which use the Virginia Standards of Learning (SOLs).
We also used the US Common Core, a multi discipline curriculum structure adopted by many of
the states within the US.
8.1.1 Virginia (VA) Standards of Learning (SOLs)
The VA SOLs are the state wide educational requirements students are expected to
learn by leaving each grade level (Kindergarten-12) until graduation, specific to each major
subject matter (English, Fine Arts, History, Math, Science). We focused on the math SOL
requirements, and became familiar with the Music related Fine Arts sections. Each grade level
has major themes that are intertwined through the students’ academic career, and some
themes have several component measures.
The state of Virginia tests students at the end of the year with statewide standardized
tests that are designed to test students’ comprehension of all themes and many if not all of the
components. The structure to identify themes and components within the Math SOLs are
Grade Level – Theme – Component – Description. So for example, ``4.2.b Identify equivalent
fractions’’ means in the Fourth grade (aged ~9 years old), the second theme has several
components, the second one of which is to “identify equivalent fractions”. We used each of
these identifiers to mark each of our own curriculum activities with the corresponding VA SOLs,
and can be seen on the top of each activity in 8.6 Lesson Plans.
The following themes and components from the VA SOLs were identified and
incorporated with our curriculum and lesson plans to administer the study and teach with SoF:
Grade 2
2.3 Identify Fractions as real numbers
1. identify the parts of a set and/or region that represent fractions for halves,
thirds, fourths, sixths, eighths, and tenths
2. write the fractions
3. compare the unit fractions for halves, thirds, fourths, sixths, eighths, and
tenths
2.20 Identify and create patterns
o The student will identify, create, and extend a wide variety of patterns
Grade 3
3.7 Add/Subtract Like denominators
o The student will add and subtract proper fractions having like denominators of
12 or less
3.19 Extend Pattern Representations
o The student will recognize and describe a variety of patterns formed using
numbers, tables, and pictures, and extend the patterns, using the same or
different forms
The Sound of Fractions
40
Grade 4
4.2.a Compare and order fractions
o compare and order fractions and mixed numbers
4.2.b Identify Equivalent Fractions
o represent equivalent fractions
o identify the division statement that represents a fraction
4.5 Factors and Simplification
o determine common multiples and factors, including least common multiple and
greatest common factor
o add and subtract fractions having like and unlike denominators that are limited
to 2, 3, 4, 5, 6, 8, 10, and 12, and simplify the resulting fractions, using common
multiples and factors
o solve single-step and multi-step practical problems involving addition and
subtraction with fractions and with decimals
4.12 Introduction to Polygons
o define polygon
o identify polygons with 10 or fewer sides
Grade 5
5.2 Equivalence and order of fractions
o recognize and name fractions in their equivalent decimal form and vice versa
o compare and order fractions and decimals in a given set from least to greatest
and greatest to least
5.6 Fractions and mixed Numbers
o Solve single-step and multi-step practical problems involving addition and
subtraction with fractions and mixed numbers and express answers in simplest
form
Grade 6
6.2 Order, Equivalence, and representation form of fractions
o investigate and describe fractions, decimals and percents as ratios
o identify a given fraction, decimal or percent from a representation
o Demonstrate equivalent relationships among fractions, decimals, and percents
o Compare and order fractions, decimals, and percents
6.4 Representations of multiplication and division
o The student will demonstrate multiple representations of multiplication and
division of fractions
6.6 Mixed Number operations
o Multiply and divide fractions and mixed numbers
Grade 7

The Sound of Fractions
41
7.12 Making Representations
o The student will represent relationships with tables, graphs, rules, and words
Grade 8
8.14 Identify relationships between representations
o The student will make connections between any two representations (tables,
graphs, words, and rules) of a given relationship
8.1.2 Common Core
The Common Core (discussed in further detail in 5.1 Common Themes in Mathematical
Instruction ) is a set of guidelines that is guided by national research and sponsored by the US
federal government, and adopted individually by most states. Each state also manages how
students are assessed against these guidelines, mostly by statewide standardized tests.
The following guidelines from the Common Core were identified and incorporated with
our curriculum and lesson plans to administer the study and teach with SoF:
Grade 1
1.MD.C.4
o Represent and Interpret Data
o Categorize data and compare categories in terms of more/less and total/whole
1.MD.A.1
o Measure Lengths indirectly and by iterating length units
o Order 3 objects by length, using a third object as reference
Grade 3
3.NF.A.1
o Develop Understanding of fractions as Numbers
o Understand 1/b as 1 part of one whole partitioned into `b’ equal parts
o a/b means `a’ parts of size `a/b’
3.NF.A.3
o Explain equivalence of fractions and compare fractions by reasoning about their
size
o Explain equivalence and comparison of fractions by size
1. a) Two fractions are equivalent if they have the same size
2. b) recognize and generate simple equivalent fractions
3. c)recognize whole numbers as fractions
4. d) Compare 2 fractions with the same numerator or denominator with <,
>, =
5. Recognize comparisons only valid when wholes are the same
The Sound of Fractions
42
Grade 4
4.NF.A.1
o Extend Understanding of Fraction Equivalence and Ordering
o Understand a/b is equivalent to same fraction multiplied by a constant number
4.NF.A.2
o Compare two fractions with >, <, = with different numerator and/or
denominator
o Recognize comparisons only valid when wholes are the same
4.NF.B.3
o Build Fractions from Unit Fraction
o a/b understand as `a’ sum of `1/b’ fractions
o understand addition and subtraction of fractions as joining and separating parts
of the same whole
o take apart a fraction that is not a unit fraction into a sum of fractions with the
same denominator in more than one way
o add and subtract mixed numbers by converting into their equivalent fraction
o add and subtract fractions having the same denominator by utilizing visual
fractions and equations
4.NF.B.4 - Multiplying a fraction by a whole number
o understand a/b as `a’ multiple of 1/b
o whole number multiplied by 1/b is a/b
o solve problems with multiplying a fraction by a whole numbers by using visual
models and equations
4.MD.B.4 - Represent and interpret Data
o Create a line plot to display unit fractions, and use this for addition and
subtraction
Grade 5
5.NF.A.1 - Use Equivalent fractions as a strategy to add and subtract fractions
o Add and subtract fractions with unlike denominators
5.NF.A.2 - Solve word problems with addition and subtraction
o Include fractions with unlike denominators by using visual models and equations
5.NF.B.3
o Apply and extend previous understandings of multiplication and division
o Interpret a fraction as a division of the numerator by denominator
5.NF.B.4 - Multiplying a fraction by a whole number or fraction
o interpret a/b x `q’ as ‘a’ parts of a part of `q’ into `b’ equal parts
5.NF.B.F.B
o Multiplying a number by a fraction greater than 1 creates a product greater than
the given number
5.NF.B.6

The Sound of Fractions
43
o Solve problems with multiplication of fractions and mixed numbers by using
fraction models and equations
5.NF.B.7 - Divide unit fractions by whole numbers and whole numbers by unit fractions
o division of unit fraction by a non-zero whole number
o division of whole number by unit fraction
o solve problems involving division of unit fractions by non-zero whole numbers
and division of whole numbers by unit fractions
5.MD.B.2 - Represent and interpret Data
o Create line plot of unit fractions and use this information and fraction operations
to solve problems using the data presented
8.2 Goals and Tasks
As we designed the curriculum, we wanted to take advantage of all of the previous
research ( discussed further in 5 Literature Review ). Some major goals we were critical to
include were:
Embodied interactions via tapping and drumming
Open ended questions and environments where the students can explore and expand
their thoughts
Group discussion, with voting, individual hypotheses, experimenting, and discussion
about hypotheses
A scaffolded yet separate approach to allow students to make gains from previous
experience to make new knowledge
Avoiding Music terminology (quarter note, whole note, etc..) and other music properties
(pitch, timbre, A through G, tempo or rate), as they conflict with other goals
Guide the students towards what is important all why asking students to identify what is
important themselves
While considering these goals, we started to identify certain tasks and activities that
would address particular properties of the system of fractions while also fulfilling themes,
components, and guidelines provided by the SOLs and Common Core. Some of the major tasks
we wanted the students to participate in were:
Make their own physical representation of their own rhythm, and try and learn what is
important to communicate to others
Tap and record their own rhythm, and see if they can recognize it when they play it back
in SoF
Get them to identify which beat comes first when presented with different information
Write down their own predictions, then interact with SoF and discuss the outcomes

The Sound of Fractions
44
Move between (transition, visualize, conceptualize, and describe) representations to see
what is conserved, what changes, and what is important
Interact with the part (beats) and the whole (rhythm) at the same time
These tasks helped us finalize each activity that is present in 8.6 Lesson Plans, but
needed to be arranged in a meaningful order (as described in 8.5 Organization and Order ).
8.3 Stages
We have designed our curriculum into three stages: (1) Creation, (2) Identification, and
(3) Manipulation. Each stage is carefully structured to properly scaffold the curriculum based
on mathematical progressions, leverage the musical skills of the students both individually and
collaboratively, present the students with meaningful musical questions that highlight the
mathematical properties needed to understand the system of fractions, and to provide a fun
and engaging ecosystem that encourages and rewards the students throughout the
assignments.
Our lab’s history with educational curriculum, computational thinking approaches, and
computer mediated learning tools XXX Citation Needed –XXX, we start our curriculum from a
completed hands-on approach, one where computers are not used. This allows for an
environment that is socially relative, familiar, and grounded in action while avoiding
distractions, technological problems, and other unwanted situations (Lee & Tatar, 2014; Tatar
et al., 2008). Since the study and accompanying curriculum is a novel and foreign situation, we
especially try to focus on the concepts we want to stress throughout the entire curriculum, and
want to capture and maintain the novelty to leverage throughout the study sessions.
Each of the stages will also be somewhat recursively nested, that is the Creation stage
will of course have activities that highlight creativity, but they will also have smaller activities or
questions that ask students to identify and manipulate their creation. Likewise, the
Identification stage will predominately ask students to use association skills, but will do so on
creations of theirs before and after basic manipulations. The Manipulation stage will focus on
different process the students can do to their creations, once they have identified what is
important.
8.3.1 Stage 1 : Creation
To help students adopt the new academic culture surrounding an embodied approach
different from their traditional mathematical instruction, we structured the tasks in stages that
help the students enter into a creative mode that acknowledges their musical skills and doesn't
focus on their mathematical skills. Math is about patterns. We engage the students in a
number of activities that focus on noticing and describing patterns. Most of our activities are
about the underpinnings of fractions, but some of them are about other kinds of patterns. The
overarching goals of Stage 1 are to have students (1) gain familiarity with description
terminology for rhythms, (2) maintain engagement, and (3) have an embodied experience of
parts and wholes at the same time.
The Sound of Fractions
45
8.3.1.1 Curriculum & Tasks
To introduce the idea of music as the central starting point of the curriculum, we will
begin by playing popular rhythms recognizable by students of the age group, with any lyrics
removed, such as Taylor Swift's Shake It Off (Swift, 2014), or Queen’s We Will Rock You (XXX
need citation XXX). We will ask the students to describe the rhythm aloud to the teacher,
allowing all students to hear the main words, concepts, and descriptions of their peers.
The teacher will then distribute sets of supplies including pen, pencil, paper, play putty,
pipe cleaners, tongue depressors, tape, and other fast prototypical materials to each student.
Each student will then individually tap a rhythm that they themselves have created, and make a
physical representation using the supplies. The students will then exchange their physical
representations, and their partner will try to tap the rhythm from purely from the information
provided by the physical representation. The creating student will try and listen to how their
rhythm is played by other students in their group. The challenge for students is that their
rhythms will likely not be played by their group members the way that the original creating
student intended. They can repeat this task as many times as time allows. The group
discussions will be focused on identifying what is important and how to strengthen their
representations to communicate their rhythms nonverbally to elicit as close to a musical
performance of the rhythm as possible.
After the discussion, we will then ask the students to come up with a new rhythm and a
modified representation that they will then again exchange. A whole class discussion will
investigate what students discovered about the challenges of getting another person to play
what they wanted. We want the students to experience the varied representations that people
have of rhythms, and that key common vocabulary exist to describe particular features of
musical rhythm, which hopefully they retain and can provide a stronger foundation to make
math analogies later. We will ask the students to write down the key vocabulary words they
learn for future reference in addition to strengthening their remembering of the description
(Dourish, 2004) in a diary that will be collected by the teacher in between sessions. If students
try and share `traditional musical' representations that come from standard musical education,
we will encourage them to make additional representations that differ substantially.
Another task will be to ask one student in a group to create a rhythm, and then have all
the members of the group to split the rhythm so that each person is responsible for an equal
part. We will then ask the students what ‘equal’ is, as there are multiple ways to answer this
within the context of a musical rhythm. Further questioning will happen to ask the students
how they divided the rhythm equally, and have them write down their process in their diary.
The tasks that are posed to the students in the creation stage focus on the students
beginning to use their own representations, vocabulary, definitions, and descriptions of
processes of fraction concepts in the context of rhythm, record their findings, and discuss and
defend their concepts with peers. This prepares them for the next stage with a stronger
collaboratively produced and academically guided concept of fractions.

The Sound of Fractions
46
8.3.2 Stage 2 : Identification
The students will now be challenged with tasks that may be easy to perform musically,
depending on their current skills, but will challenge them to describe the key features and
process in mathematical terms they identified in the previous stage as well as mathematical
concepts that they may not have been able to comprehend previously. Also, tasks that utilize
SoF challenge students to use digital representations of their music that more closely resemble
classical mathematical representations.
8.3.2.1 Curriculum & Tasks
To help segue to the new stage, we will start with a pigtailed task that allows students
to play around with the interface to get acclimated with the interface and simply play. Many
students will be able to pick up on the majority of the functionality during playing around, but
each directed task will provide detailed instructions for task completion throughout the stage.
Students will record be able to record their rhythm and perform their rhythm by tapping on the
desk. Students will then be asked to describe and manipulate their rhythms, and to create
complementary rhythms with additional instruments. Many activities involve switching roles to
help focus on both parts of the whole, what is theirs, and what is not. Just as in the first stage,
some discussion will take place in person, and some hypotheses and descriptions will be written
in their notebooks.
Other scaffolded activities include carefully structured problems that challenge students
to identify the particular attributes of the beats (individually and collectively, both on and off),
the different patterns for each instrument, and the rhythm as a whole. Guided discussion
alongside the scaffolded activities will allow them to see alternate descriptions of the fractional
components of the rhythms, as well as the preparing them to change the rhythms with greater
accuracy in future dynamic activities. Strengthening students’ common vocabulary allows for
them to investigate the changing situations that come along with manipulating their rhythms in
the next stage.
XXX- all the other tasks and their descriptions of what they accomplish
8.3.3 Stage 3 : Manipulation
In our proposed new curriculum, students tapped individually and collectively in a group
by themselves with increasing amounts of instruction, and then progressed to activities that
involved guided identification of specific mathematical properties. Now the students will move
into a technologically mediated environment that challenges them to use their robust musical
skills to grow and defend more mathematical language by manipulating multiple visual
representations that represent their musical performances.
8.3.3.1 Curriculum & Tasks
XXX- all the other tasks and their descriptions of what they accomplish
Upon completing the final stage and thus all activities and the entire study, students will
gain a stronger ability to create, identify and manipulate their own representations, those

The Sound of Fractions
47
created by others, and more traditional representations that come up in various contexts and
scenarios. The third stage helps with this by focusing on moving between representations,
describing the important attributes that surround the parts and whole in situ (not sure if this is
clear, I meant the contexts that the fractions exist within), recalling situations with similar
problem spaces, and considering multiple perspectives of the parts and whole.
8.4 Do, Ask, Takeaway
In order to plan transportation, purchase and organize materials, delegate
responsibilities, identify important goals, provide important questions to ask, and provide for
on the fly changes, we designed a lesson plan structure that follows the Do, Ask, Takeaway
model of XXX Citation Needed XXX. Each lesson plan begins by asking the students to ‘Do’
some task, sometimes accompanied by instruction. After performing the tasks, the students are
then posed questions that are designed to target particular attributes, ideas, features, or
mental processes that align with the activity and goal. Both the ‘Do’ actions and the ‘Ask’ goals
are oriented to get the students to ‘Takeaway’ a particular idea after completing the activity.
The blank activity sheet in Figure 8-1 (originally done by hand as shown in Figure 8-2 )
that the activities are all structured around has a title section for the name of the activity, along
with sub headings for the associated SOL themes and components, the location, day that the
activity occurs on, the number of the activity it occurs in relation to the other activities for that
day, and the projected duration of the activity. The left side has an area to include all materials
needed for the particular activity, the setup instructions for that activity, any facilitator notes
(and an area for the facilitator to take notes during the activity). The main section is divided up
into three sections of Do, Ask, and Takeaway. Some activities require two or three instances of
the Do activity, so there is an appropriate number of subsections if the activities or questions
differ slightly based on which iteration is occurring.

The Sound of Fractions
48
Figure 8-1 A Blank Activity sheet that follows the Do, Ask, Takeaway model. It has areas for
materials, setup, notes for the facilitator, location, day, activity number, projected duration, a,
the name of the activity, and the associated SOL themes and components

The Sound of Fractions
49
8.5 Organization and Order
Using our goals and ideas of tasks ( described by 8.2 Goals and Tasks ) as a guide to
elaborate on our activities and three stage structure ( described in 8.3 Stages ), we needed to
work through designing each activity and the order to properly scaffold the students’ learning
progressions.
8.5.1 Cut ups, Card Sorting, and David Bowie
Matching appropriate lessons to our available study participants (number of students,
groups, locations, and resources available) is not an easy task. It can not simply be made a rigid
structure, nor a top-down approach to solving the structured order. It also can not be a loose
approach or a bottom-up approach to design the scenarios. The rapid changing situations of
schools, administrators, and after school programs requires flexibility, but this characteristic
should not negatively affect the students in a negative manner.
To provide the most flexibility for real time adjustments while adhering to the three
stage structure of our curriculum, we made individual papers of each activity and [re]arranged
them to categorize and order them. This also allowed us to adjust them by splitting some
activities into multiple activities,
Figure 8-2 An example of an activity prior to being complete, with sections for Do, Ask,
Takeaway, Supplies, and general notes

The Sound of Fractions
50
Figure 8-3 Most activities on a temporarily taped on a dry erase board to allow for moving
around, categorization, order, and editing during the final stages of plaaning for the overall
curriculum and lesson plans.
8.6 Lesson Plans
After all of the conceptualization, planning, and organization, the final curriculum was
devised. We designed them to be flexible for the needs of the study participants, and
meaningful progress given the short segmented time frames of the study. Please see 15.4
Curriculum for the entire curriculum.
9 PROGRAMMING AND UI
With the conceptual idea ( discussed in 6.2 Redesign and Conjectures ) and curriculum (
discussed in 8 Curriculum ) in a stronger structure, we began working on strengthening the
second iteration of the online program, the Sound Of Fractions. This section is to describe the
many obstacles, choices, and solutions we developed to get to a fully working educational tool
that would allow us to teach fractions alongside music creation and satisfy our research goals
and questions.
9.1 Informal Areas
To begin developing a robust software development approach, we needed to first look
at the areas of interest for our study ( as described in 7 The MAIN Study ). From a
programming standpoint, the main areas of interest are software development life cycles that
The Sound of Fractions
51
accompany team developed large scale robust applications, the User Interface (UI), and
planning for the User Experience (UX). This concerns can not be completely separated from the
curriculum, so they were done in parallel with the curriculum development, harnessing the
greatest potential from both while considering and identifying limitations.
9.2 Programming
To address the programming concerns and requirements for this study, we addressed
the architecture and UI to match our intended curriculum and UX goals.
9.2.1 Architecture
To accommodate the robust requirements of multiple manipulable graphical
representations and synchronized animations in a highly configurable microworld, the
architecture quickly grew complex. We needed to develop reusable components that took
advantage of DRY (Do not Repeat Yourself) coding styles and functions that fit in a proper
structure. The architecture soon moved to a structure that is analogous to a live symphony,
and so many of our components are named after the matching roles or actions of an orchestra
with some references to the recording industry as well. Some of the names are displayed in the
UI, while many exist only in the code base, not user facing, but aids development with stronger
naming conventions.
The Stage is where the magic happens. It has a conductor, and instruments (used and
unused), and a button to reset everything back to the initial state, often used when starting a
new activity, and sometimes used when a bug prevents further interaction.
The Conductor is represented by the Play/Stop button, as it communicates to all
instruments when to play or stop. It is up to each instrument to manage its own animations
and sounds.
The Instrument (also known as a H[orizontal]Track or Track) consists of several UI
elements and an underlying matching sound. There is an icon to help students reinforce what
they are interacting with, a text label, as some students may not recognize the instrument by its
look and shape, and a container for all of the Measure Representations to be aligned. We call
this container the Measure Representation Collection, and this is where the default Audio
representation will be, along with any other representations the user adds.
The Measure Representations are individual representations located within a particular
instrument, in the form of one of the five representation types: Audio, Bead, Line, Pie, or Bar.
The Measure Representations for each instrument all share the same underlying rhythm, and
have graphical components that represent the whole (via the larger circle [for the audio, bead,
and pie], the line length, or the bar outline) and the parts (each individual beat via a flash, small
bead, line tick, pie slice, or bar piece).
The Whole is the graphical representation of the entire rhythm’s duration. The term
measure is avoided in the UI, curriculum, and discussion, as it pertains strongly to musical
The Sound of Fractions
52
notation and terminology, and can confuse students who need to focus on the whole, and not
what constitutes a musical measure.
Each Beat is individual to its Measure Representation, but it is also the SAME beat
[sound, order, and idea) across all Measure Representations of the same Instrument. This
allows each corresponding beat to animate during playback or toggle (turn on or off) during
interaction at the same time. In other words, the third graphical beat in one Measure
Representation of a Bead Representation (the third bead) shares the same underlying sound as
the third graphical beat in another Measure Representation of a Pie Representation (the third
pie slice), and will both turn on or off if either is clicked, and will both move at the same time
when the rhythm’s order comes to the third beat unit.
The Instrument Generator container allows the users to add a new instrument when
needed or desired, and it is automatically returned here when the user removes an instrument
from the stage, providing a consistent approach to dealing with a finite number of mutable
instances.
The Stamps container is holds all of the labels that we allow the students to drag and
drop (stamp) onto the representations when trying to
The Representations container holds the icons of the different representations that are
available. These are available to use when a user wants to Add a representation to a current
instrument, or when the user wants to Transition a current Core Four representation into
another.
Other general background requirements include a link to the homepage via the title,
and a login button to provide more specific user tracking.
9.2.2 Application Specifics
This research has been developed for many years, and as a result, there have been
many implementations for different areas of the research, mainly documentation, SoF
application, and the data viewer. To support this robust approach, we used many technologies,
frameworks, and libraries.
9.2.2.1 Sound of Fractions Main Application
Backend is run by:
Ubuntu: 14.2 Virtual Machine (VM) server
Node.js : A JavaScript server to provide easier communication between the clients,
server, and database
Upstart : Serves continuous updates and handles server crashes
Git : Deployment of production code
Sequelize : A node package to communicate with the database.
JS-Cookie, Node-UUID, Crypto-JS : A node package to handle logging of users until they
log in, as well as if thy lose internet connection temporarily.
The Sound of Fractions
53
HTTPS Certificate : an SHA-256 certificate under Virginia Tech for a secure connection
MySQL : a database for storing the users, their rhythms, and log each interaction, served
on a different port of the same server
Winston : A node package for extra verbose logging for debugging
Front end consists of:
Framework
o Backbone.js : manage the data structure, and document object model (DOM)
layout and views
o Underscore.js : a requirement for backbone, as well as knowing the order of the
beats that students manipulate on their rhythms
UI
o D3.js : To draw, animate, and transition the different graphical components
required for the students to interact with
o Bootstrap : Framework for creating organized and responsive pages with
structured HTML, CSS, and JS
o JQuery (JQueryUI) : Manipulation of the different graphical components required
to label the representations and manipulate the rhythms
o Font Awesome : a text font that provides graphical icons as a selectable font
Audio
o HTML5 Audio – Mozilla’s code to utilize the laptop audio (HTTPS required)
o Soundcloud : a database of open source sounds to make the audio rhythms
Browser
o Chrome : Google’s we browser that takes advantage of Mozilla’s HTML5 Audio
o Chrome DevTools : used to develop and validate SoF web application
9.2.2.2 SoF Data Viewer
AngularJS – A framework for developing sites focused on making front end developer’s
work easier.
CrossFilter – For filtering multidimensional data
Parse – An online backend database that uses RESTful approaches
Lightbox – for providing a photo viewer and browser
HTML5 Video – For displaying the videos of transitions
9.2.2.3 Documentation and General Development Tools
GitHub : a repository to mange code for redundancy and multiple developers
Sublime Text 3 : a text editor for writing code
OmniFocus : for making visualizations of the curriculum, data, and teaching material for
developers

The Sound of Fractions
54
Word (2016) – a word processor for writing this document
Homebrew – A mac based package manager
LaTeX (MacTeX) – An open source writing tool and compiler for making complex written
documents
Fake Data Generator – A Sublime Text package to generate structured seed data
MySQL Workbench – to manage, view, and edit the database
Gource – An open source visualization tool for look at code contributions by people over
time ( see 15.7 Main Code Branch Development Timeline Video for the video itself)
Adobe Creative Suite (CS6 – Photoshop, Illustrator, InDesign) – A suite of applications
for making posters, pictures, drafting, and public facing documents
Mendeley – an online tool for managing citations
BibDesk – a open source Mac based citation manager
ZamZar – Word to HTML converter. Free, and AWESOME. Word 2016 fails with large
documents, ZamZar delivers
9.2.3 Data Collection
The four data types (video, diaries, artwork, and logs) were collected during the study
via a method suitable for each type. Classroom activities were recorded on a digital camcorder
and organized into meaningful contributions from the students with loose transcriptions. The
making of the physical representations (Artwork) was supplied with general crafting materials
and pictures taken with accompanying notes if provided by the student. Interaction logs were
stored in a backend MySQL database in sentential form with every action accompanied by the
state of their rhythm and accompanied graphical representations in JSON (JavaScript Object
Notation) format.
9.3 User Interface (UI)
To account for all of the different main components (as discussed in 9.1 Informal Areas
), the final UI came together with the play/stop button, the Stamps section to label, the
graphical representations to add or transition to, the Stage area where instruments were
placed, and the collection of measure representations for each instrument. Instruments not
needed were held in an area below instruments that were being used. A reset button and login
area were also provided. You can see many different situations that are occurring during a
typical activity in Figure 9-1 .
The Sound of Fractions
55
Figure 9-1 The final UI design of SoF with a Snare instrument with 5 alternating beats, a High
Hat with 4 alternating beats, an unused Kick Drum, and both used instruments having all 5
representations present, currently not playing/animating.
9.3.1 Color
The color choice was chosen as a result of several discussions and smaller UX studies.
We are not confident that our choice is the best, nor are we confident that there is a stronger
candidate, or that including color itself has the strongest gains.
9.3.1.1 Our Color Choice
Our major study included a color palette choice for beats that are ordered, and cycle
through sets (arrays) of three based on red, green, and blue (RGB) variations, so that there is
always distinction between the individual, with the last (blue) variation is perceptually different
from the next following first (red) variation in the array, with problematic colors removed. The
Hexadecimal values of our array are: 1: "#FF0000" (red), 2: "#00ff00" (bright green), 3:
"#0000ff" (blue), 4: "#ff0080" (hot pink), 5: "#80ff00" (light green), 6: "#00ffff" (light blue), 7:
"#660000" (maroon), 8: "#FF7722" (light orange), 9: "#0080ff" (med blue), 10: "#808000"
(olive), 11: "#00ff80" (Turquoise), 12: "#ff00ff" (magenta), 13: "#EE4000" (dark orange), 14:
"#FFD700" (yellow), 15: "#006600" (michaels green), 16: "#8000ff" (purple). These can be seen
in Figure 9-2.
The Sound of Fractions
56
Figure 9-2 The color palette of beats in order 1 through 16
The main motivation for this choice is to emphasize the order, scalar, proportionate
properties, consistency, conservation, and supporting polymorphism. This ensures that during
the instruction, the facilitator can both inquire and reiterate these fractional properties across
multiple representations and activities. This can be accomplished through questions like
• Which comes first?
• Describe the red beat.
• Which green beat comes first?
• What color (or position) is the eighth (or light orange) beat before and after you
transition the representation?
• Why are the last beats in all of your individual representations the same color?
• Why is the last beat of your representation(s) a different color from your neighbor’s
last beat color?
This helps us emphasize:
• The first beat is red no matter which representation.
The Sound of Fractions
57
• The red beat is the first beat no matter which representation (1/n always comes first)
• The second beat (bright green) follows the first beat (red) (2/n always comes after
1/n)
• The first beat (red) precedes the second beat (bright green) (1/n always comes before
2/n)
• The order remains the same no matter how many beats (parts) (1/n is followed by
2/n, followed by …, until n/n no what the size of n)
• The order remains the same no matter what size of the rhythm (whole) (1/n is
followed by 2/n, followed by …, until n/n no what the size of n/n)
9.3.1.2 Other Color Options
We also considered to describe the colors representative of the color wheel, so that a
beat in the XXX. This would then translate from linear progression along linear representations
relative to circular representations’ circumference in radians. We also considered greyscale,
but the look seemed to bland and disengaging. We did include the greyscale beats to signify
beats that are off. We unfortunately did not account for protanopia, deutaronopia, or
tritanopia color blindness for representing the colors of the beats.
9.3.1.3 Color in Current Typical Mathematics Representations
Looking at printed textbooks available to students, standard graphical mathematical
representations that are presented to elicit or inquire about fractional qualities are typically
XXX-Cite text book from Emily)XXX
9.3.2 Stage
We limit the number of instruments to three, as it is an optimal number that provides
the following:
• Maximum usage of the vertical real estate available on a typical laptop resolution
and aspect ratio
• Distinct sounds that are perceivable by students regardless of their musical skills
• An excellent number to pose mathematical problems in an abstract form, such as a
+ b = c, a(b) = c, a>b>c, and other equations (in different forms such as word,
sound, and static and animated visuals) that are important for a strong
understanding of the system of fractions
9.3.3 Representations
We have developed five different graphical representations [Audio, Bead, Line, Pie, Bar]
to elicit particular mathematical and computational properties (Wing, 2008) for a musical
rhythm. All representations have unique properties, but the Audio is different from the other
four [Bead, Line, Pie, Bar], as it focuses on representing the temporal and cognitive idea of the
rhythm, not focusing on graphical elements. We call the other four the `Core Four'.
The Sound of Fractions
58
All representations can be presented on screen for a particular instrument [Snare, High-
Hat, or Kick Drum], and the representations are linked, meaning that they each represent the
same rhythmic pattern recorded for that instrument. If the underlying rhythm is changed, all
representations will update. This can happen when a new rhythm is recorded, a beat is added
to or removed from the rhythm, a beat is toggled between playing (sounding) or when resting
beats (not sounding) occur.
All representations can be removed from the instrument by clicking the minus (-) sign in
the upper right, allowing students to create arrangements of representations with particular
representations juxtaposed next to other. The Audio representation has a recording button
(finger tapping logo) in the lower left to allow the student to record over the current rhythm for
a particular instrument. The Core Four have a pile of remaining beats in the lower left, allowing
the students to add beats to their rhythm; the Audio rhythm is spatial-temporal based, and
therefore can't have beats to grab from, making it the candidate for the recording button, as a
button that represents the translation from the temporal and cognitive rhythm in their head to
the computer.
The Core Four also have the ability to stretch or shrink, changing the playback length,
which gives the effect of speeding up or slowing down the tempo of the rhythm pattern. The
handle to adjust the size (limited to horizontal manipulation for the one dimension [linear]
representations [Line and Bar] and limited to equal linked horizontal and vertical manipulation
for the two dimension [circular] representations [Bead and Pie]) is in the lower right. The
stretch or shrink manipulation waits until the student is done dragging to adjust all other
representations to the same final size. This is the only manipulation that does not propagate to
the other Core Four representations in real time, because if they did, and had at least one Core
Four representation to the left, that representation would grow simultaneously, causing the
manipulated representation to shift.
The Sound of Fractions
59
9.3.3.1 Audio Representation
The spatial-temporal component of a rhythm should not be ignored, as a beat that
resides solely in a cognitive state can not and will not be communicated for others. Children
who are exposed to music and music education show improvement in spatial temporal
reasoning skills in fractions (Graziano et al., 1999). We provided this visual metronome that is
linked to the performance of any beat as a way to aid the student in seeing and feeling the
music as a real time performance by the computer. It also can serve as a feedback notification
when tapping the beats on the table near the computer, as microphone settings or the distance
to the computer may need adjustment to ensure proper recording.
Figure 9-3 The Audio representation present in SoF

9.3.3.2 Bead Representation
This is our novel contribution. Modeled from necklaces, bead making, and the rosary
beads during our ideation design sessions, it has many features that are attractive. Beads [and
by virtue beats] can be added to or removed from the circle [whole], completely changing the
properties of whole circle. Simply increasing or decreasing the count by one drastically makes
the mathematical properties quite different. Even if a student taps an easy pleasing pattern in
halves, fourths, unlikely sixths, or pushing the system and going to the full limitation of 16
beats, a single manipulation will enter them into much harder musical patterns and
mathematical concepts of a whole, thirds, fifths, sevenths, or fifteenths.
9.3.3.3 Line Representation
The Line representation is the first in the selection of representations that the students
will notice as familiar, but not totally the same. We do not call it a number line as there are no
numbers, as the student can make the determination themselves where to place the reference
points. This will be illustrated by taking a straw and threading it over a taught string tied
Figure 9-5 The Line representation present in SoF
Figure 9-4 The Bead representation present in SoF
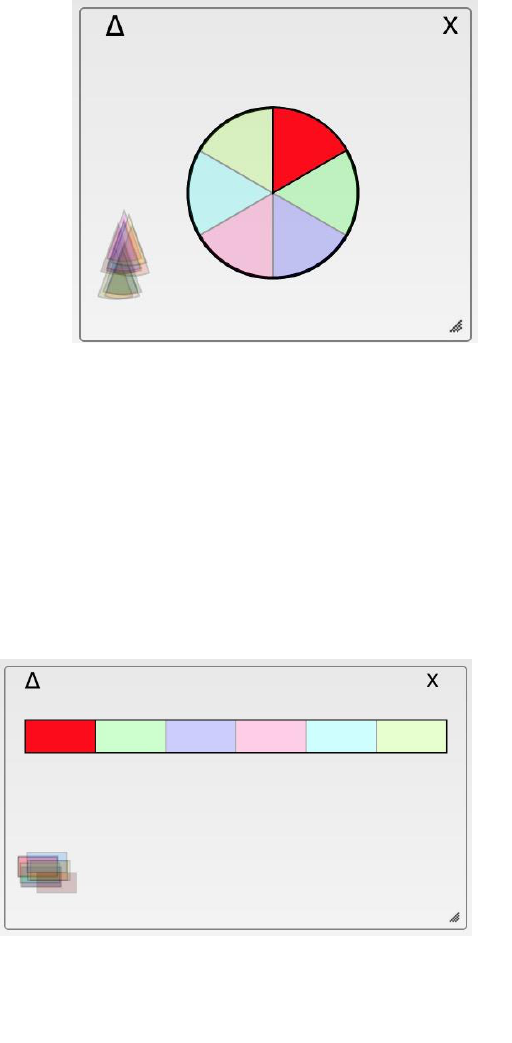
The Sound of Fractions
61
between to points, with the straw having delimiting marks but no labels. The string will have
marks evenly spaced at the length of the straw, allowing the students to move the straw along
the string and choosing the reference points.
9.3.3.4 Pie Representation
The Pie representation, the fourth button available to the students to choose, is the first
fully recognizable representation, as the pie shape is the most prevalent representation used to
teach fractions, as it can be referenced as a food (e.g. a pizza, a circular fruit, a cookie, etc...), a
geometrical circle, or any other circular object that could be feasibly split (e.g. a clock, a bag of
marbles, coins/tokens, etc...).
9.3.3.5 Bar Representation
The Bar representation is another fully recognizable form factor that students in the US
will have already been exposed to extensively in math curriculum and class. This
Figure 9-6 The Pie representation present in SoF
Figure 9-7 The Bar representation present in SoF
The Sound of Fractions
62
representational for easily maps to word problems that involve candy bars, sticks or rods, and
certain distance problems.
9.3.4 Transitions
The Core Four also can be transitioned from one representation to another in a
graphical transition that shows the important stages highlighting what is conserved and what is
lost, and strengthening the understanding of what each representation has to offer. The idea
of conservation originates from Piaget's conservation experiment, in particular Grouping VII,
which deals with equilibrium [equivalence] (what is the same), combinativity (the concept of
things as combined group rather than individual pieces), associativity (order doesn't matter in a
group of equal parts), identity (a unique part), and reversibility (a part has an inverse) (Papert,
1980). We provide mechanisms to highlight conservation during the graphical animations of
the representations, which have clear delineated stages to show transformation, a graphical
transition where no forefront properties are added or removed, only the shapes are deformed [
a circle is cut and unrolled into a line] ), replacement, where one form of a beat (a bead circle)
is replaced by another form (a number line tick), removal, when an important feature is
removed (a graphical element representing a division is removed), addition, when a new
important feature is included in the representation (when a graphical element representing
duration is added).
Upon reviewing the transitions, we have come to realize that each of the Core Four offer
different yet important characteristics. As previously stated, the Line and Bar share linear
characteristics, while the Bead and Pie share circular characteristics. Two other characteristics
the Core Four afford are duration and division. The Pie and Bar representations highlight the
duration of each beat, where the eye is drawn to the size of each beat, and the divisional lines
are minimized graphically. The Bead and Line representations highlight the divisions in the
whole rhythm pattern, as the spacing between each beat is emphasized more strongly than the
beat, drawing the student to see the separation as more important.

The Sound of Fractions
63
Figure 9-8 A comparison of the representations and their transitions with relative properties
To our knowledge, this is also a novel contribution, particularly within the D3 (Data
Driven Documents JavaScript) community. To accomplish the animation of a circle unrolling
into a line, we make a path (consisting of a series of coordinates) of a line, and add a path of a
circle that moves horizontally along path of the line over several stages (each stage
representing a frame in the animation). We then combine the first part of the line with the
remaining front part of the circle to achieve the needed coordinates for the path to appear
unrolling. If you were to consider the circle (known to be a geometrical shape with an infinite
number of sides) to have less sides, such as eight, the stages will look like Figure 9-9:
The Sound of Fractions
64
Figure 9-9 Unrolling a circle into a line with fewer frames and less reference points.
To accommodate both the different (generally not strong) computational capacity of
various computers used during the study and the different number of beats that are on a
representation (trying to get even degrees of separation around the circle with one to sixteen
beats), we dynamically generate the path to provide the best possible combination of the
highest number of frames (between 39 and 48 [calculated by the number of beats that divides
equally into a number closest to 40 without exceeding 50]) and the number of coordinates
along the path (approximately 120) to provide the highest fidelity circle with the most fluid
simultaneous transition animation of the path AND the beats along the path.
9.3.5 Beats and Rests
During exploration of parts and wholes, it is inherent that the problems begin to have
discretion about the parts that make up the whole, otherwise students can not see beyond the
homogeneous whole. In curriculum, the majority of mathematical problems distinguish the
parts in a binary manner (i.e. `haves' and `have nots'). Thus, our implementation has to discern
any differences we choose to support. We decided to also maintain binary parts, and thus we
support the `haves' as beats, a graphical representation whose shape is based on the
representational type of the rhythm (e.g. a Bead beat is a small bead as in , a Pie beat is a small
pie slice) with full opacity with an accompanying sonification of a particular instrument for a
particular amount of time, and the `have nots' as rests, the same graphical representation size

The Sound of Fractions
65
and shape of a counterpart beat with partial opacity and an accompanying perceived amount of
time where no sound is produced. For this paper it should be noted that in our discussion,
unless otherwise noted, we refer to BOTH beats and rests as a beat or beats, as discerning
becomes more import in context of a particular problem or situation.
9.3.6 Playback
Playback is quite important for the students. A play and stop button allow for repeated
sonification and graphical animation from the beginning, as well as visual and aural cues about
the mathematical and musical properties of the rhythm they have physically create using their
hands and recorded or using the interface to arrange beats into a rhythm representative of
their cognitive rhythm. During playback of the rhythm, the beat representations animate in
ordered fashion, the first beat in each representation moves respective of its whole measure
and returns to the original position during the time allotted for the individual beat or rest,
followed by the second, and so on. This ordered animation supports the idea that the graphical
beat occupies a specific amount of temporal space noted by the time it plays, a physical space
noted by the physical graphical space it occupies, as well as having an auditory landscape of a
particular instrument represented by its sound.
10 RESULTS
During the smaller trials, research of prior works, involved in discussions with other
research projects within the Third Lab, and involvement in several research projects, certain
data was planned to be collected and analyzed.
10.1 Demographic Information
We conducted the current main study in the Fall of 2015 in southern Virginia. The
county is predominately of a low SES where the large majority of jobs are outside of the county
itself. We worked with a local community center to communicate with the school system and
active community members to identify two prospects for the study. We worked with a local
elementary school and a local church afterschool program.
10.1.1 Census Data
The county has a population of about 20,000 and 92% are Caucasian and 6% Black or
African American. 75% of the population 25 years old or more have a high school diploma,
while only 10% have a bachelors or higher. The average time to work is 26 minutes. The
average number of people in a household is 2.32 and the average total household income is
35$,000 USD. (“No Title,” n.d.-a).
10.1.2 Education System Data
The county has four elementary schools (K-7), one primary school (K-3), one upper
elementary school (4-7), and one high school (8-12). All schools have been fully accredited by
the state board of education, meeting or exceeding state expectations for public schools. The

The Sound of Fractions
66
county school system operates on a budget of $29-30M (“No Title,” n.d.-b). The average cost
per pupil is reported as $10K.
School System
Number of students
2600
% on Free Lunch
47%
% on Reduced Lunch
10%
Table 10-1 Education system data of the number of students, and the percentage on free and
reduced lunch
10.1.3 Student Demographic Data
We conducted one study at an elementary school, referred to as Group 1, and one at a
local church’s afterschool program, referred to as Group 2.
Group 1 students were identified by the principal and teachers as needing extra help in
mathematics, and were already enrolled in a special extra remedial math class to help them
individually with their math development. The research instruction occurred for about 45
minutes before school officially ended, followed by a break to receive a small snack (juice and
crackers) and then return for an afterschool session. Some students were unable to participate
on certain days due to school wide functions, transportation issues, other afterschool program
conflicts, or sickness.
Group 2 at the local church is an ongoing effort from members of the community to
offer additional educational opportunities and provide a meal to families who would like to
take advantage of this resource. For some students, this service will include an important meal.
The students ride a bus to the church provided by the local school system, and then eat a meal,
and then participate in activities. The students are then picked up by their parents/guardians.

The Sound of Fractions
67
Group 1
Remedial Class/Afterschool
Group 2
Afterschool
Number of students Starting
8
12
Number of students Ending
7 (1 white male grade 6 left
after Day 4)
11 (1 white female grade 6
left after day 3)
# | % of White
8 | 100%
8 | 66%
# | % of Black
0 | 0%
3 | 25%
# | % Hispanic
0 | 0%
1 | 8%
Average total time of
instruction per session
93 minutes (with a break of
about 10 minutes)
66 minutes
Number of Sessions
7
6
Age Range
11 - 13
11 - 13
Grade Range
6 - 7
6 - 7
Boys # | %
4 | 50%
7 | 58%
Girls # | %
4 | 50%
5 | 42%
Table 10-2 Student Demographic Information of the two groups
10.1.4 Attendance and Participation
The consent and assent conditions of our Institutional Review Board (IRB) allow students
and parents to abstain from a single activity, the entire class, or the program as a whole, at
their own discretion. As a result of this, one student in Group 1 was requested by the parents
to no longer participate in the study midway through. One student in Group 2 also was no
longer allowed to participate due to behavioral issues. Transportation issues also restricted
participation to the first remedial class session consistently for one student in Group 1. Their
data up until they stopped participating is still presented, but limited because of participation.
10.2 Data Sources
The main types of data that were collected were
Video (notes and observations of in class interactions),
Computer logs of interactions with SoF (every important interaction coupled with the
state [before and after] of their rhythm and representations),

The Sound of Fractions
68
Journal notes (hand written and drawn answers to questions asked during class), and
Artwork and other manipulations (their physical constructions and completed handouts)
These four data sources were then each analyzed, compared, and contrasted with each
other to initially identify common themes.
10.3 Themes Present in Each Data Source
Reviewing the different data sources provided a start to our analysis of our research
interests. We must evaluate our data and study from several perspectives to understand our
learning environment that we created, along with the various situational micro-worlds students
participated in throughout the curriculum. Some perspectives relate to the people involved:
students, teachers and administrators, and researchers. Other perspectives include the
addition of our aural and physical contexts. And of course, we must inspect the mathematical
concerns as a primary motivation for our work.
We grouped these themes based on their overarching perspectives we are trying to
incorporate. We considered educational, design, sensory, musical, and mathematical
perspectives. We also considered the similarities between particular themes and grouped them
by similar concepts within their own perspective. Educational perspectives include teaching
[teachers and administrators] as well as [student] learning. Design has many facets, but we
focus on the visual elements for our analysis. We only found evidence for visual, physical,
aural, and gustatory senses. Like our literature search, there remained little to no evidence of
olfactory data in our observations. Musical perspectives include the patterns of the music as
well as the musical musical components and attributes that actually make up the music
students create and work with. The mathematical perspective includes the system of fractions
and the current perspectives of cognitive schemes children employ to work with fractions. We
judged how strong of a presence a particular concept exists within each data source, and can be
seen in Table 10-3 and Table 10-4.

The Sound of Fractions
69
Perspective
Concept
Theme present in data source
Data Sources
Video
Notebook
Logs
Artwork
Education
Teaching
Spend more time on a subject [5]
STRONG
-
-
Medium
Clarification (Teacher to students) [6]
STRONG
-
-
STRONG
Clarification (student to student) [8]
STRONG
-
Medium
STRONG
Learning
Confusion [10]
STRONG
STRONG
weak
STRONG
Incorrect Information [8]
STRONG
STRONG
weak
weak
Correction [12]
STRONG
STRONG
STRONG
STRONG
Notable Learning Moment [10]
STRONG
Medium
Medium
STRONG
Design
Visual
Orientation (linear/circular) [12]
STRONG
STRONG
STRONG
STRONG
Colors [9]
Medium
weak
STRONG
STRONG
Senses
Aural
Descriptions [8]
STRONG
weak
weak
STRONG
Sound [11]
STRONG
Medium
STRONG
STRONG
Visual
Label [11]
STRONG
STRONG
STRONG
Medium
Animations [8]
STRONG
weak
STRONG
weak
Physical
Tangible [7]
STRONG
weak
-
STRONG
Manipulations [11]
STRONG
Medium
STRONG
STRONG
Embodied [8]
STRONG
weak
Medium
Medium
Gustatory [5]
Medium
Medium
-
weak
Table 10-3 Section A of themes, concepts, and perspectives present in each data source
The Sound of Fractions
70
Perspective
Concept
Theme present in data source
[Weighting score of all data sources]
Data Sources
Video
Notebook
Logs
Artwork
Musical
Pattern
Type/Categorization [10]
STRONG
STRONG
STRONG
weak
Size/Quantity [12]
STRONG
STRONG
STRONG
STRONG
Component
Pitch/Timbre [3]
weak
-
-
Medium
Speed/tempo [10]
STRONG
Medium
STRONG
Medium
Volume/Intensity [8]
Medium
Medium
weak
STRONG
Mathematical
Fractional
Order [9]
STRONG
Medium
STRONG
weak
Scalar [11]
STRONG
Medium
STRONG
STRONG
Part [12]
STRONG
STRONG
STRONG
STRONG
Whole [9]
Medium
STRONG
STRONG
weak
Literature
PUFS (Partitive Unit Fraction Scheme) [4]
Medium
Medium
-
-
EPS (Equipartitioning Scheme) [4]
Medium
Medium
-
-
Splitting Loop [5]
STRONG
Medium
-
-
79
54
52
61
Table 10-4 Section B of Themes present in each data source. A STRONG rating equals 3 points, a
Medium rating equals 2 points, a weak rating equals 1, and 0 points are assigned to data that
does not show evidence of being present with -. The totals are tallied vertically for each Data
source, and horizontally for each theme.
10.3.1 Evaluation of themes and data sources
It became clear that all themes that were of interest exist in at least two data sources. A
weighted evaluation of 3 points for STRONG, 2 points for Medium, 1 point for weak, and 0
points for no evidence of presence provides a basic quantifiable measurement of the strength
of perspectives, concepts, themes, and data sources.
10.3.1.1 Themes, Concepts, and Perspectives
The weakest themes surround pitch/timbre of music, and the evaluation of the
presence of mathematical learning schemes. This may highlight the actual lack of presence in
the data sources in addition to our lack of expertise in these particular fields to recognize
meaningful presence. The strongest themes were Correction (learning moments when
students corrected their statements, hypotheses, findings, approaches, etc…), Orientation

The Sound of Fractions
71
(discussion and interaction surrounding the linear or circular placement of objects),
Size/Quantity (discussion and interaction including the size or quantity of elements or groups),
and Parts (discussion and interaction involving the parts of a rhythm or fraction). Other
noticeably present themes include Sound (performing or interacting with sounds), Labels
(attempts to use alternative representations to describe an ideas or objects), Manipulations
(acts of direct manipulations of something already completed or presented to students) and
Scalar (discussion and interaction surrounding the scalar properties of rhythms and fractions).
This highlights that our approach has both a varied and important presence in each of the
perspectives that we want to discuss during our curriculum.
To consider the concepts and perspectives as a whole, we aggregated the themes by
their concepts, and tabulated the results, shown in Table 10-5. The weakest concept remains
gustatory (and may be argued as an outlier against our overall study and goals). Other lower
scores (Teaching, Visual [Design], Aural, Visual [Senses], Patterns, and Components) do not
show signs of being weaker than the others, rather a consistent baseline, scoring very close to
each other and accounting for sixty percent of the concepts (6/10) and fifty percent percent of
the themes (14/28) we identified.
We also aggregated the perspectives with regards to their concepts in the same
method. This highlights that our focus is not as strong in the design perspective. It also shows
that the sensory perspective is quite strong in relation to our other perspectives.
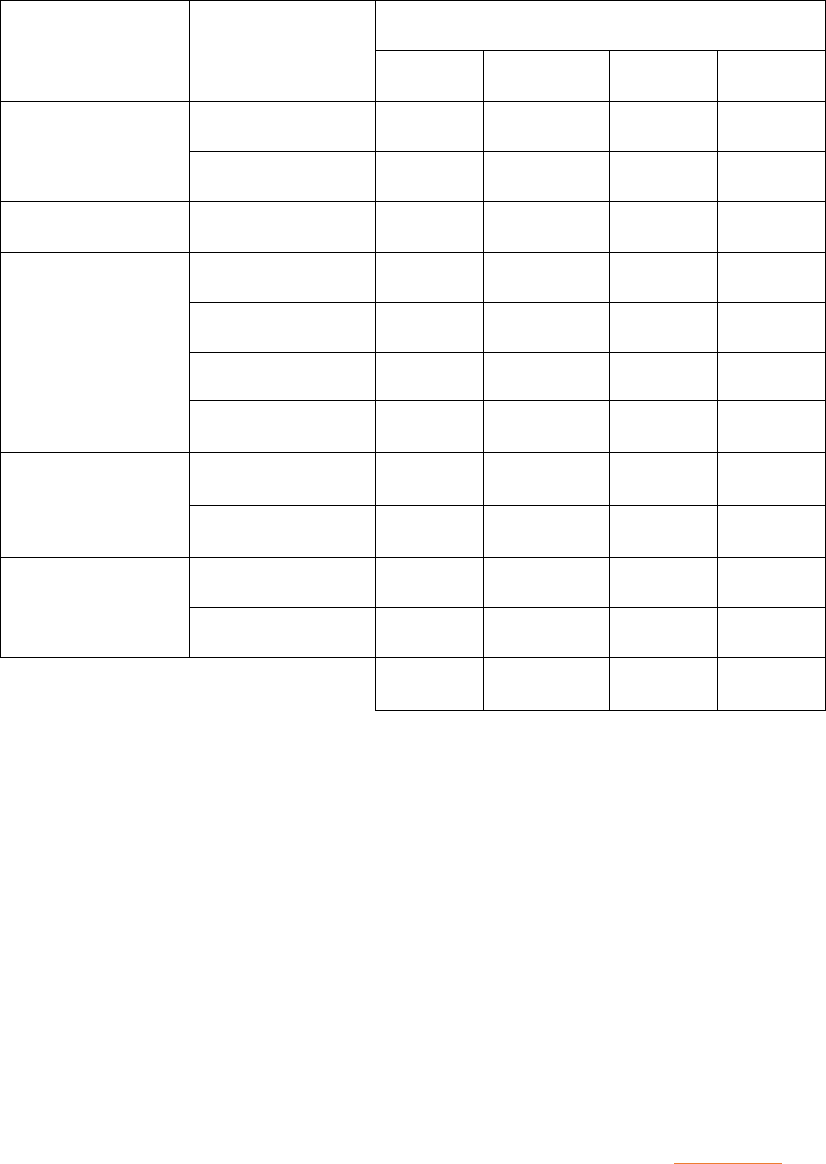
The Sound of Fractions
72
Perspective
Concept
Data Sources
Video
Notebook
Logs
Artwork
Education [59]
Teaching[19]
9
-
2
8
Learning[40]
12
11
7
10
Design [21]
Visual[21]
5
4
6
6
Senses [69]
Aural[19]
6
3
4
6
Visual[19]
6
4
6
3
Physical[26]
9
4
5
8
Gustatory [5]
2
2
-
1
Musical [43]
Pattern [22]
6
6
6
4
Component [21]
6
4
4
7
Mathematical
[44]
Fractional[31]
11
10
12
8
Literature[13]
7
6
-
-
79
54
52
61
Table 10-5 Weighted ratings of a higher level Perspectives and their underlying Concepts per
each data source.
10.3.1.2 Data Sources
Adding the scores for each data source also makes a contribution. The Video data
source has the largest concentration of themes present, followed by Artwork, and the
Notebook and Logs are relatively equivalent. This motivates us to focus more on the artwork
and the Video data more so than the notebooks and logs. This is beneficial as there are more
(and richer) data points to consider in the front runners. This doesn’t not deter us from the
other two, as they have very rich contributions relevant to their medium and context.
10.4 Curriculum
The curriculum, exercises, and study as a whole as described in the Curriculum section
was analyzed for consistency, effectiveness, areas of opportunity, student engagement, current
knowledge, and learning. In this section we deconstruct the days and activities as it pertains to
the all students, the groups, and a select few students from each group who highlight the
benefits of using SoF as a robust teaching curriculum.
The Sound of Fractions
73
10.4.1 Group information
We designed each curriculum activity with a projected amount of time each activity
should last, accounting for, transitional periods, setup, questions risen by students, and other
classroom management concerns. Given the differences in the structure between both groups,
the order of the activities was adjusted slightly to accommodate the time students were
available, student attendance and participation, school maintenance closings, national holidays,
the direction of the students’ interest and questions, technical problems, and other unforeseen

The Sound of Fractions
75
10.4.1.1 Group 1
Students in Group 1 had seven sessions with an average session length of 101 minutes
(1 hour and 41 minutes) with an average of 93 minutes (1 hour and 33 minutes) of actual
instruction time. Due to the nature of the class structure, Group 1’s sessions were setup to
span across the school day’s official end time. The first part, approximately 40 minutes, was
part of a remediation class, and the second was part of an after school class, lasting
approximately 60 minutes. This structure is the main reasoning behind the intermediate
break(s) between class instruction during the study. Most breaks consisted of the students
going to another area for a short time (10 minutes or less) to grab a snack and bring back with
them.
Given the extra time that Group 1 has in comparison to Group 2 (approximately 30
minutes) we were more lenient on pushing the curriculum as strong with regards to timing, and
allowed for more instruction that was directed by students’ inquiries.
For a complete overview and detail documentation of the events that occurred in the
classroom, please see 15.5 Group 1 Video Data and Notes.
10.4.1.2 Group 2
Students in Group 2 had six sessions with an average session length of 66 minutes (1
hour and 6 minutes). The structure of Group 2 being in an afterschool program at a local
church, the students would receive a school provided bus ride to the church, and then would
eat a large snack (sometimes serving as the student’s only dinner meal). The students that
participated in our study only made up about thirty percent (30%) of all students, and so some
weeks we provided music based activities that were appropriate for all ages at the afterschool
program, as most students and volunteer understood us to be associated with music learning
activities. This is the reasoning for some of the shorter sessions that have substantially less
time (days 4 and 6).
For a complete overview and detail documentation of the events that occurred in the
classroom, please see 15.6 Group 2 Video Data and Notes.
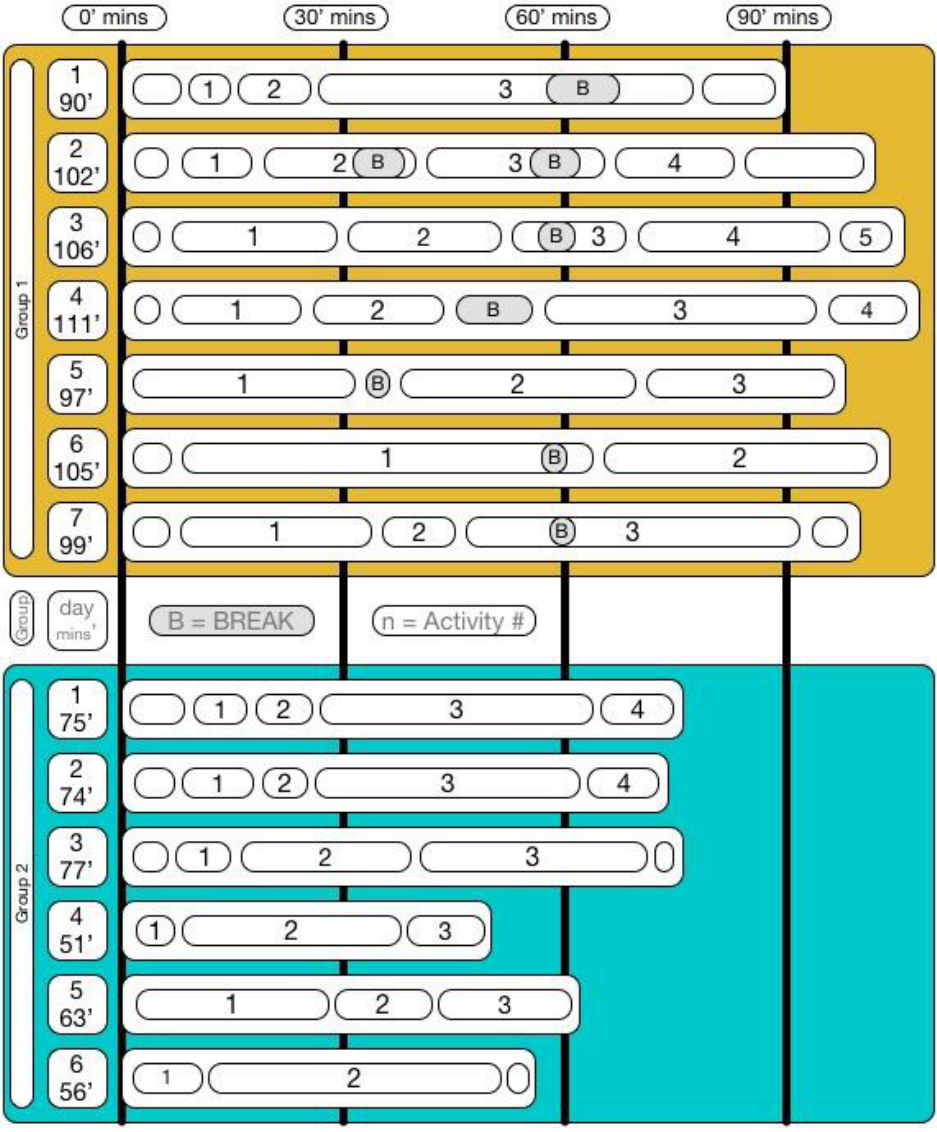
The Sound of Fractions
76
Figure 10-1 Overview of both groups study sessions, including the overall elapsed time of the
day and individual times for activities
The Sound of Fractions
77
10.4.2 Activities that students excelled at
10.4.3 Activities that students struggled with
Which activities or sub activities were unsuccessful?
What does it mean to be unsuccessful (talk about failure to grasp takeaway?
10.5 Learning Moments
The main purpose of our research is to make meaningful tools to help children learn
fractions. The answer is not as simple as yes or no, but we believe that overall we definitely
made strong positive measures and improvements in the students’ knowledge and
understanding of fractions. We can say this from look at pre-post inquiries, the explanations
students provided as the study progressed, the struggle and perseverance displayed along with
the ‘ah hah!’ moments, discovering XXXX
10.5.1 Pre-post Test – What are fractions
When we began the study, we began with music playing in the background playing, and
talked a bit about our research to help the students relax. Interestingly enough, several
students began tapping (feet and writing utensils) while signing the assent papers. This let us
know immediately that they were enjoying the music. To help us understand where the
students are, both individually and collectively as a group, we asked the students to define
what a fractions is, what it means to them, why it is important, and what their favorite fractions
was if they had one.
Student descriptions of fractions were varied but predominately short, misspelled
definitions.
10.5.2 Student Explanations
10.5.3 Activities that students excelled at
10.5.4 Activities that students struggled with
Which activities or sub activities were unsuccessful?
What does it mean to be unsuccessful (talk about failure to grasp takeaway?

The Sound of Fractions
78
11 DATA ORGANIZATION AND VISUALISATIONS
Given the plethora of data types and ensuing data, a need arose to present the data in a
structured, meaningful, and useful manner to allow for analysis, recall, and discussion. We
separated the data into:
• Classroom activities – video analysis which were digitized into graphical
visualizations
• Diaries - their notes, hypothesis, and written answers to curriculum activities and
questions
• Logs – sentential structured data of students interacting with SoF
• Artwork - Physical representations the students created of their own rhythms
11.1 Video Data
Each group was recorded during the study with two video cameras, a digital camera,
and instructional notes. To be able to quickly reference the information that occurred at a high
level with relevant information (such as student participation, voting, absenteeism, answers,
general observations, etc …), we notated each interesting idea on paper by hand, and evaluated
this method after two sessions. This enabled us to concentrate and refactor our observations
according to particular cues. We actively avoided full transcriptions, as the software and
techniques associated with them focus on more quantitative analysis, where we are interested
in more qualitative approaches. We then organized this data by each group, each day, and each
activity to show each student’s contribution (as noted by us according to our cues noted in the
initial reviews) during each activity (and sub-activity). Several thoughts, discussions, and
guesses were left out of these data records, mainly those that were not seen as a noticeable or
verifiable clue as to what the student was thinking (such as off topic discussions, shouting
random guesses, or sayings of ‘I don’t know’ without a hint of what the student does know).
You can find a legend of the layout and the many components of the video data in Figure 11-1.
For a complete overview and detail documentation of the events that occurred in the
classroom, please see the corresponding sections for each group: 15.5 Group 1 Video Data and
Notes and 15.6 Group 2 Video Data and Notes.
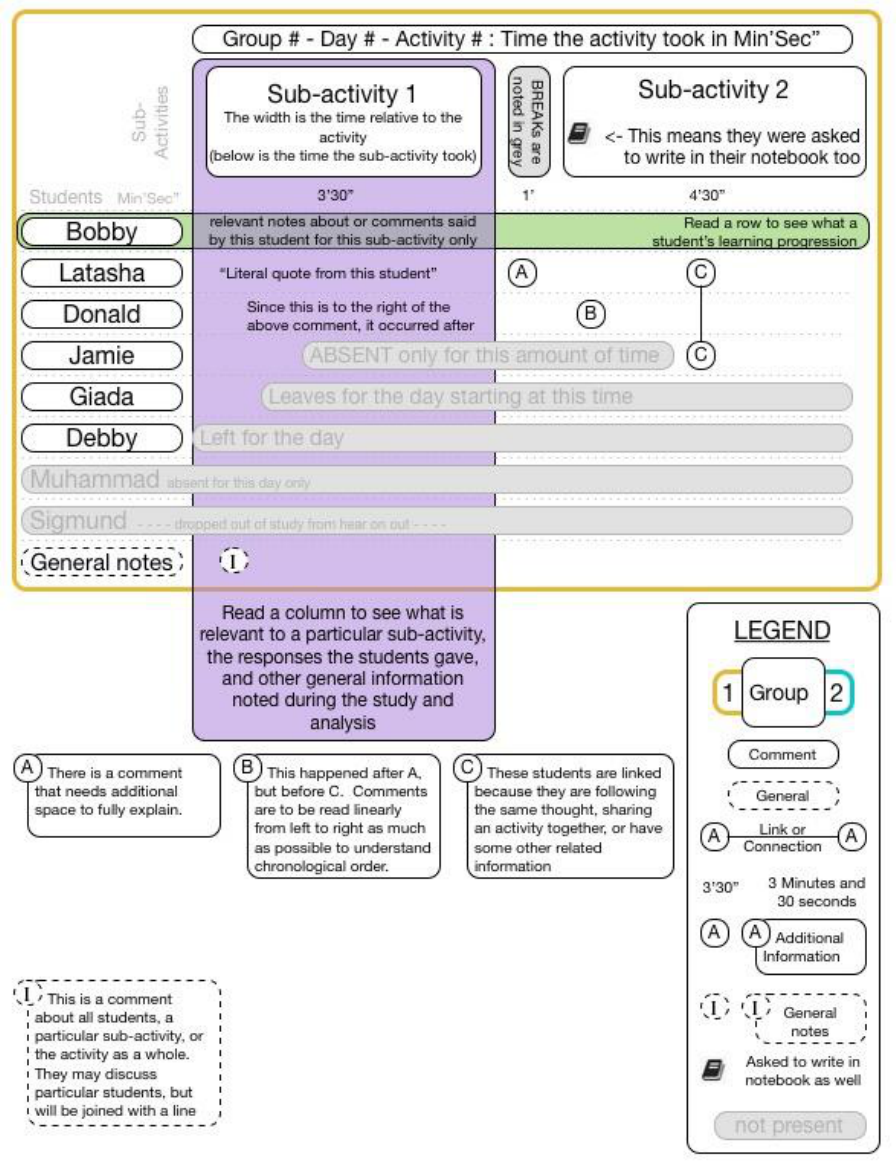
The Sound of Fractions
79
Figure 11-1 A legend of the structure of data of the video analysis of each activity of each day of
a each group, including students, sub activities, contributions, and general notes, with notations
of accompanying diary entries.
The Sound of Fractions
80
11.2 Notebooks and Artwork Data
XXXX explain the organization of notebook and artwork data XXXX
11.3 Log Data
Log Data was collected during usage of the online interface of SoF. Students were told
that the interactions were being logged, but that they didn’t need to worry about it. The
logging system kept track of interactions we were interested in, such as
adding, removing, or toggling a beat,
adding, deleting, or transitioning a representation,
adding or deleting an instrument,
starting, stopping, and duration of playing a rhythm,
stretching or shrinking a rhythm,
adding, adjusting, or removing labels,
recording a rhythm,
or general administration information such as logging in
The log message was stored with information about
The student performing the interaction,
The interaction itself in sentential form with pertinent information,
A JSON string of the student’s rhythm,
And a Date and Time stamp of when the interaction occurred,
and sent to the database for storage, with backup plans for internet connectivity issues. We
collected 17851 interactions during the study.
A sample log sentence looks like:
Stopped playing music. Duration of playback in seconds: 3.648 and the song
lasts 3.204 seconds for a total playback number of 1.138576779026217 times.

The Sound of Fractions
81
And a sample JSON String of their rhythm looks like:
{
"usedInstruments": [
{
"label": "Snare",
"active": true,
"signature": 4,
"tempo": 120,
"measures": [
{
"beatsArray": ["ON","OFF","ON","OFF"],
"numberOfBeats": 4,
"measureRepresentations": [
{ "currentRepresentationType": "audio", "transitions": 0 },
{ "currentRepresentationType": "bead", "transitions": 0 }
]
}
]
},
{
"label": "Hi Hat",
"active": true,
"signature": 8,
"tempo": 120,
"measures": [
{
"beatsArray": ["ON","OFF","OFF","ON","OFF","OFF","ON","OFF”],
"numberOfBeats": 8,
"measureRepresentations": [
{ "currentRepresentationType": "audio", "transitions": 0 },
{ "currentRepresentationType": "pie", "transitions": 0 },
{ "currentRepresentationType": "line", "transitions": 0 }
]
}
]
}
],
"unusedInstrumentsCount": 1
}
From the collected data, we were able to analyze the following:
The distribution of rhythms made by students with a particular signature
The distribution of recorded rhythms by duration
The comparison of rhythmic complexity (how many equal parts [beats on and off])
against the number of beats tapped (how many times the student actually tapped)
The number of instruments used in each rhythm
The representations being visualized in each rhythm
The number of times a rhythm was transitioned
Speeding Up versus Slowing Down Rhythms
Rhythm duration scaled in terms of original duration in terms of x
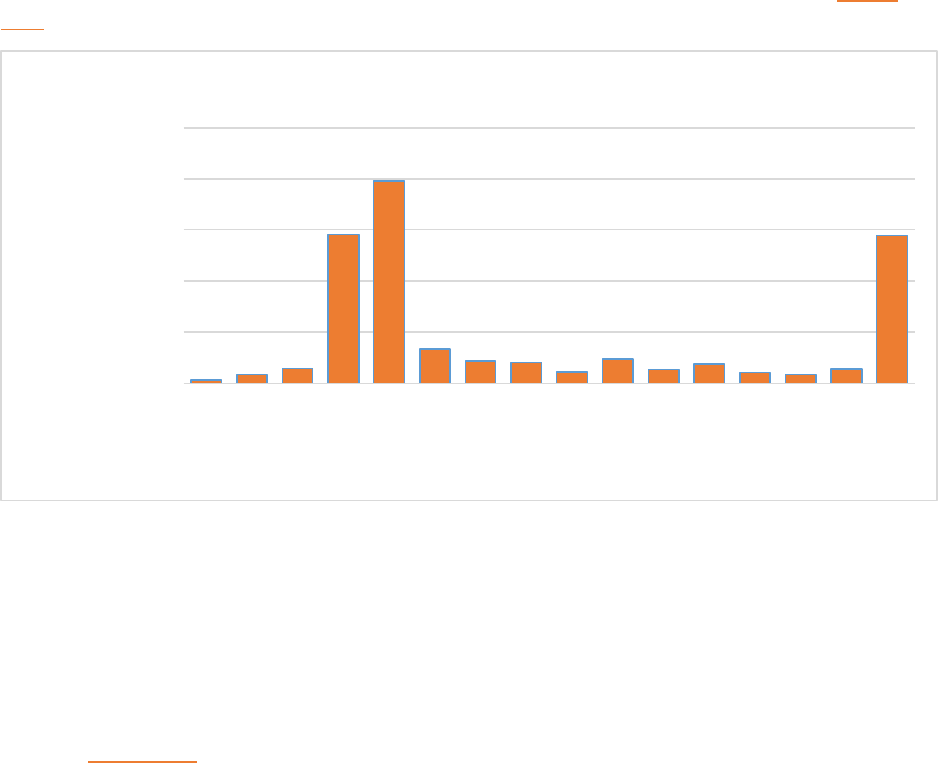
The Sound of Fractions
82
11.3.1 The distribution of rhythms made by students with a particular signature
Every interaction was analyzed for the instruments used, and each of their signatures
(the number of beats [on and off] that are in each measure of each instrument) was tallied.
Each instrument’s default signature was 4 beats, leaving the signatures of 5 and 16 being the
most prevalent. The signatures of 16 also involve the upper limit of SoF due to graphical real
estate limitations, and are likely also attractive for students given the upper limit, colors used,
and musical complexity. The rhythms with a signature of 5 are most likely due to the
curriculum and student choices focusing on this rhythm. These results can be seen in Figure
11-2.
Figure 11-2 Distribution of Rhythms by Signature
11.3.2 The distribution of recorded rhythms by duration
To look at the recordings of each student, we studied the duration of each student’s
recorded rhythms. In general, students tapped shorter (less than 4 seconds of percussion)
rhythms. Altogether, there were 125 recorded rhythms during our study. These results can be
found in Figure 11-3.
131
338
576
5814
7930
1349
868
827
449
944
538
740
420
350
553
5785
0
2000
4000
6000
8000
10000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Number of occurrences of a
rhythms
Signature (number of beats [on or off] in a rhythm)
Distribution of rhythms by Signature
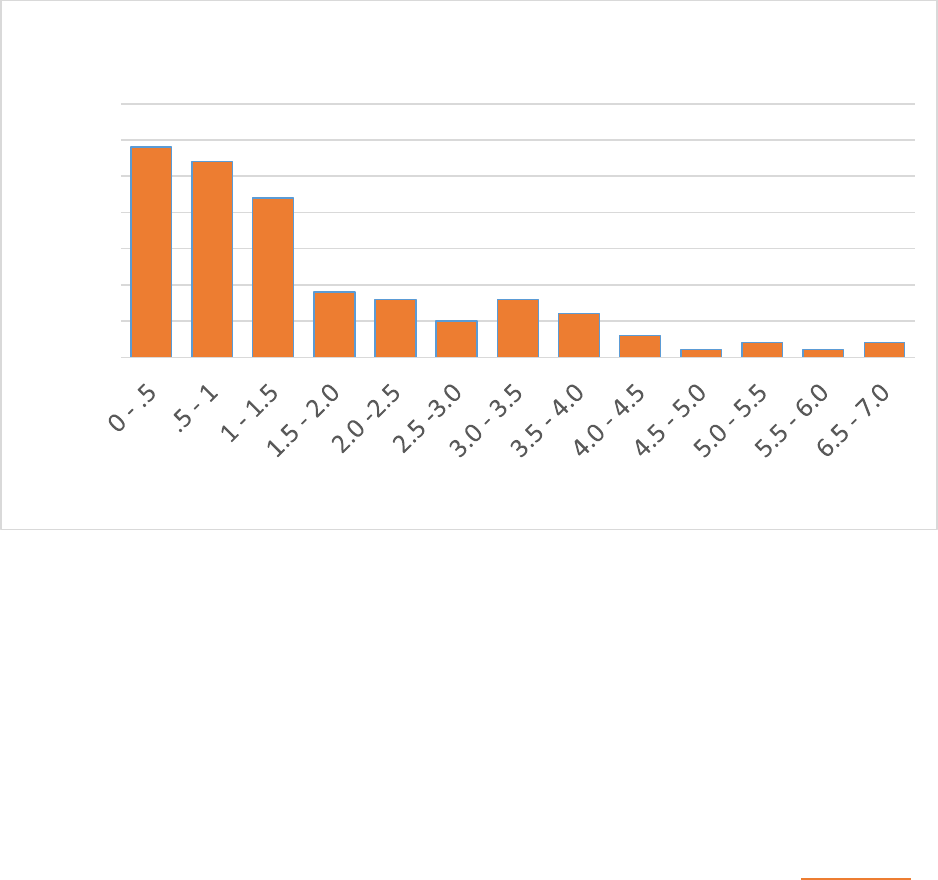
The Sound of Fractions
83
Figure 11-3 Distribution of recorded rhythms by duration
11.3.3 The comparison of rhythmic complexity against the number of beats tapped
Knowing the duration is a good start, but we began interested in the musical complexity
of some rhythms that were recorded. Thirty-six rhythms were complex enough that they
needed to be trimmed to the first sixteen beats to be compatible with SoF. However, students
did not always tap beats evenly. Some students tapped rhythms that had few beats, but with
different musical patterns, reflected in a rhythm with more parts than tapped. Although
complex in performance, SoF would only play back the first sixteen equal units, so students
often adjusted their rhythms to something less complex. This data can be seen in Figure 11-4.
29
27
22
9
8
5
8
6
3
1
2
1
2
0
5
10
15
20
25
30
35
Number of rhythms
Duration of a recorded rhythm in seconds
Distribution of recorded rhythms
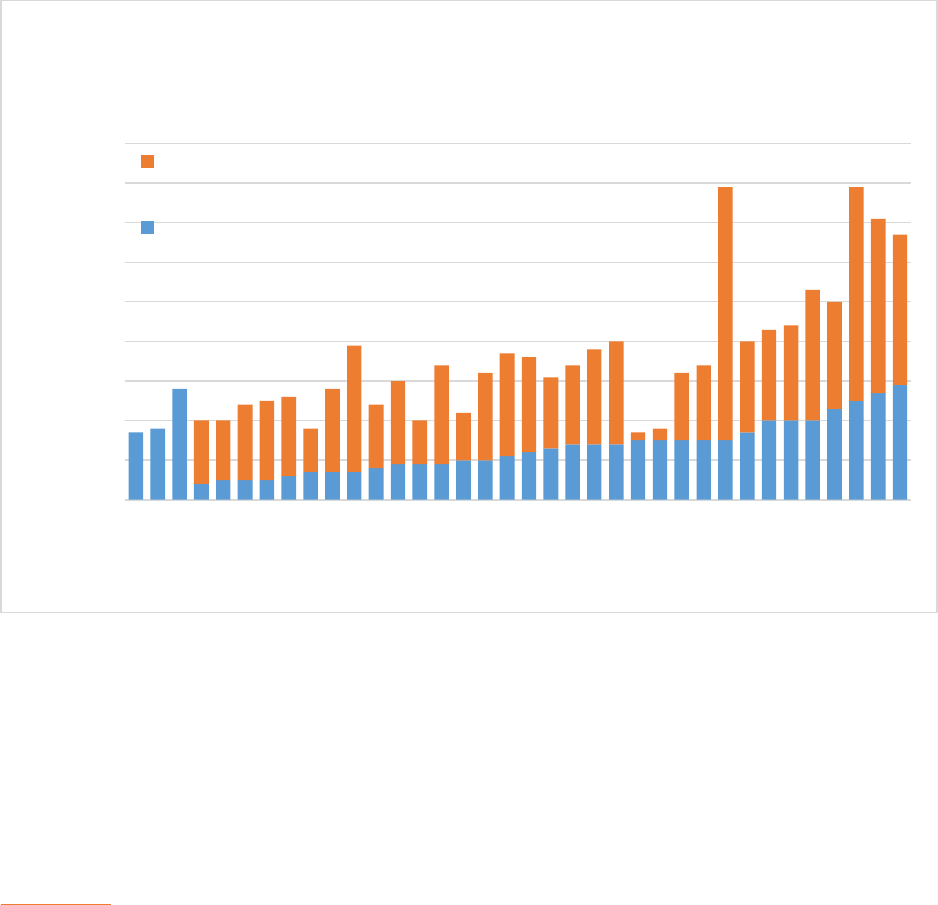
The Sound of Fractions
84
Figure 11-4 The comparison of rhythmic complexity against the number of beats tapped
11.3.4 The number of instruments used in each rhythm
Students were able to navigate the Stage quite well, adding and removing instruments
as they interacted with SoF. Although their stage was seeded with 1 instrument, and some
activities included interacting with multiple, it is informative to know that students know both
boundaries but predominately interacted consistently with 1 instrument. This can be seen in
Figure 11-5.
0
10
20
30
40
50
60
70
80
90
Number of beats in a song (complexity)
|-----|No normalization More Beats tapped & More Normalization----->
( 36 rhythms total )
Recorded Rhythms requiring trimming to 16 beats (limit of SoF)
Comparing Complexity (with number of beats) vs Normalization
After Normalization (number of beats perceived with rests)
Before Normalization (actual number of beats tapped)
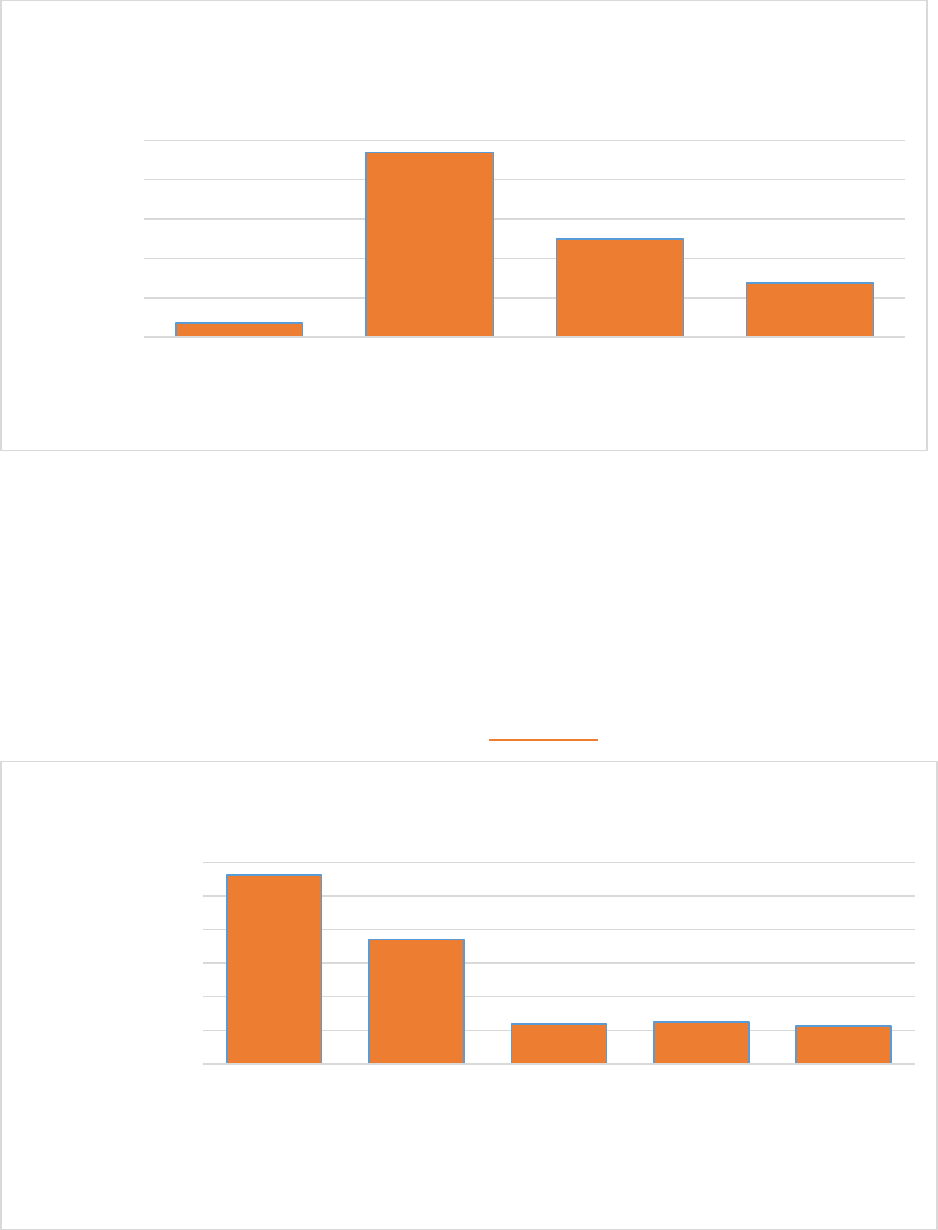
The Sound of Fractions
85
Figure 11-5 The number of instruments used in each rhythm
11.3.5 The representations being visualized in each rhythm
When students start SoF or add an instrument, there is an Audio representation that
supplied with it. Many of our curriculum activities focus on the bead representation. It is a
great parallel that our program helps take a cognitive and embodied rhythm and visualizes it
the most, but also reinforces our goals of using more traditional mathematical representations
via our Bead representations. This can be seen in Figure 11-6.
Figure 11-6 The representations being visualized in each rhythm
724
9386
5000
2742
0
2000
4000
6000
8000
10000
0 1 2 3
Number of occurrences of a rhythm
Number of instruments used in a rhythm
Number of Instruments used in each
Rhythm
28160
18483
5944
6162
5639
0
5000
10000
15000
20000
25000
30000
Audio
(Default)
Bead Bar Line Pie
Number of
Representations used
Representation Type
Representations used in Rhythms
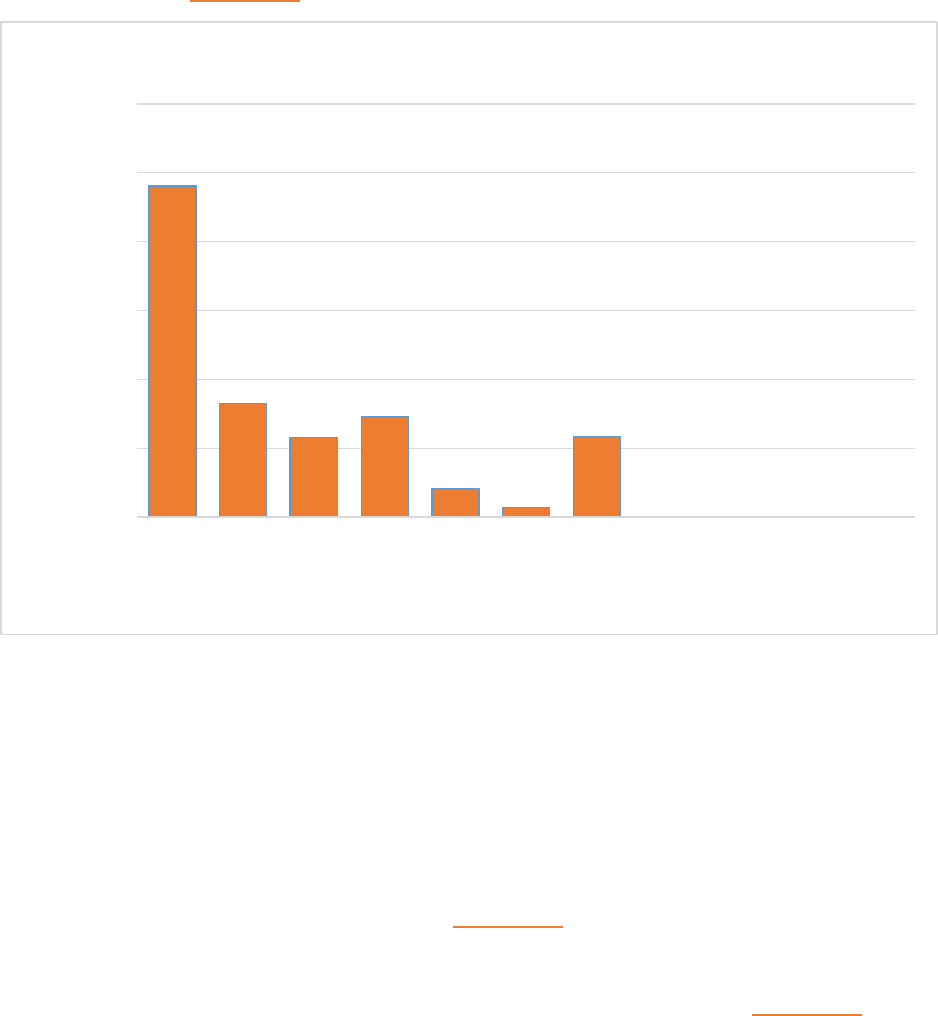
The Sound of Fractions
86
11.3.6 The number of times a rhythm was transitioned
Understanding what a rhythm is can be experienced through an embodied, cognitive,
entrained, visual, and mathematical approach. Each of these approaches have multiple
perspectives. SoF supports multiple mathematical and visual perspectives through our
representations, and transitions between them. Our curriculum only asked to transition once,
so it is important to see that students transitioned many of the representations multiple times.
This can be seen in Figure 11-7.
Figure 11-7 The number of times a rhythm was transitioned
11.3.7 Speeding Up versus Slowing Down
SoF supports many mechanisms to adjust the musical characteristics of their rhythm.
An important mathematical and musical adjustment is the ability to stretch or shrink the
representation to increase or decrease the playback duration, giving the aural and visual
appearance of speeding up or slowing down the rhythm as a whole. Students stretched the
rhythms more than shrinking them, as seen in Figure 11-8. This means they made the rhythm
appear visually larger. This however makes the rhythm play slower (more distance to travel at
a constant rate. Students ultimately operated with songs that were less than 1x of the original
duration of their rhythm (recorded or graphically made). This can be seen in Figure 11-9. This
shows that the visual interaction supports two different concepts: usability teaching, and
musical interest/complexity. The interface correctly teaches the students through visual and
961
331
231
293
82
28
234
2
1 1
2
0
200
400
600
800
1000
1200
1 2 3 4 5 6 7 8 9 10 11
Number of Occurrences
Number of transitions (62112 represntations with 0 transitions)
Number of times a representation was Transitioned

The Sound of Fractions
87
aural feedback that the larger the representation means the slower of the rhythm and the
smaller the representation means the faster the rhythm. The musical interest and complexity
is show by the fact that students chose operate with rhythms that are more complex in
[perceived] tempo.
Figure 11-8 Speeding Up vs Slowing Down Rhythms
Figure 11-9 Rhythm duration scaled in terms of original duration in terms of x
125
169
Speeding Up vs Slowing Down
Speed Up (make smaller visually) Slow Down (make larger Visually)
152
109
24
9
0 0
1
0
20
40
60
80
100
120
140
160
0-1 x 1-2 x 2-3 x 3-4 x 4-5 x 5-6 x 7-8 x
Number of rhythms scaled
Amount scaled in terms of x (1.5x = 150% of original duration)
Rhythms durations scaled to in terms of x

The Sound of Fractions
88
12 DISCUSSION
With the curriculum made ( see 8 Curriculum ) and the data collected and organized (
see 10 Results ), we began to analyze everything for important themes, data that proves our
hypotheses, and other notable phenomena.
12.1 Research Questions
During the development of SoF as a whole, we began to realize that there are certain
interactions that have great potential for learning moments, direct questions that will challenge
the students to think abstractly and beyond their traditional mechanisms for solving problems,
and areas of exciting potential when moving from musical and embodied interactions towards
the goal of more standard mathematical representations and discussions. We began to inquire
about several questions based on our conjectures:
How can a micro-world that utilizes additional representations provide meaningful
resources for learning, and address misconceptions that are blocking student learning?
Can students who struggle with fractions make meaningful progress in their
composition, comprehension, and communication when approaching the system of
fractions from perspectives related to music?
How do multiple, novel, rich, and interactive culturally appropriate representations
affect engagement in a learning environment?
12.2 Research Question 1: How can a micro-world that utilizes additional
representations provide meaningful resources for learning, and
address misconceptions that are blocking student learning?
We want to investigate how SoF provides meaningful advantages in contrast to the
current ecology that is not fully addressing certain students in their academic endeavors. This
requires us to look at the current environment students are exposed to, what students choose
to operate with, and what our approach supports.
12.2.1 Contexts in Math [Education] Domain
Our study started with extensive reviews of math literature on current and
comprehensive math education resources. Out of these readings we cam to understand the
current academic thinking of how students perceive and approach fractions, and where some
main barriers exist. Reviewing the resources available to teachers via textbooks and other
media, it is clear that the majority of education in the math domain with regards to fractions is
not robust.

The Sound of Fractions
89
12.2.1.1 Where Does Sound of Fractions Fit In
Our research indicates that the main components of fractions are the the unit fraction
(1/n), the parts (all the 1/n s), the whole, the part and the whole together, and the
relationship(s) between the part(s) and whole(s). To understand fractions at a competent level,
one must be able to contextualize the situation, identify the important components and ignore
the non-important ones, and describe the identified components in a meaningful way. The
person also must be able to manipulate these components by iterating the parts, separating the
whole into parts, and ordering them appropriately for the context of the situation they
identified.
To teach these skills, fractions are taught in the classroom with word problems,
numbers and equations, graphical elements, or stories about real life examples that students
likely have some form of varying participatory experience. Teachers and administration can
measure the student’s fraction competency by asking the student to solve an equation or
problem, properly label a graphical element, or perform mental math to understand how well
the student knows fractions. We would like to note that it is quite difficult for any one person
to properly design and assess a particular facet of any fraction learning scheme that a student
may be using. It is difficult because the instructor must have a well rounded understanding of
fractions themselves, as well as how to provide a teachable moment to a student when there is
a struggle to understand or perform, as well as a way to test the newly communicated concept
in a different way that strongly highlights if a student understands the concept, and not a rigid
process (i.e. not just changing the variables or numbers in an equation, but changing the
equation itself). Our outline of what fractions consist of and the approach in the math domain
are shown in Figure 12-1.
The Sound of Fractions
90
Figure 12-1 The system of fractions and its major components on the left. A
representation of how the math domain is currently represented, implemented, and measured
on the right, with the Sound of Fractions unsure of how to properly fit in the math domain.
Using this understanding of how math is currently being approached in an educational
setting is what fueled our initial design. The initial prototype failed academically however
because we failed to have academically structured lessons. It did however flourish with
opportunities beyond engagement, highlighting the students’ creativity, exploration, and
continuous interest. This leaves an interesting question. How does Sound of Fractions fit into
the math domain? By trying to include SoF into the math domain with appropriately guided
curriculum, it became apparent that it fits quite well. During the study it became clear that
students also excel in understanding fractions in other contexts too.
12.2.1.2 Other Learning Contexts That Students Can Operate and Learn in
Current approaches in the math domain are meant to teach, with the knowledge
ultimately ending up in the CONITIVE domain of the body, also known as knowledge. There are
many ways that we can gauge knowledge that exists in the cognitive realm through different
communication mediums. People often use hand gestures and utterances in communicating
the ideas and problems we are working through in the mathematical domain to help aid our
efforts with higher fidelity channels (such as verbal and written). We identify five contexts that
are relevant to math education, some that have particular attractive features for fraction
learning: Visual, Aural, Physical, Gustatory, and Olfactory, all based on the five senses. We also
identify the temporal qualities of each of these contexts as they relate to the cognitive domain.
Most of the current math domain is represented in VISUAL contexts. They are exhibited
in the form of word problems, equations, numbers, shapes, graphs, icons. These
representations can be performed by the student by viewing or creating animations, labeling
them, or solving equations or problems.
SoF brings in an entirely new context, AURAL. We do this by providing curriculum that
starts with listening to music first. This experience provides a base for an environment that
highlights the entraining nature of music, so the students can experience the whole rhythm and
the individual beats at the same time. The study participants, like even younger children, are
able to perceive the repeating rhythm rather than just individual beats or chaotic noise.
Our curriculum goes one step beyond listening to music. We provide PHYSICAL
representations and performances by allowing students to participate in music making with
embodied interactions, both individually and as a group. We allow them to tap multiple
rhythms, and adjust them in the interface by dragging new beats on to a rhythm, dragging
beats off of a rhythm, stretching the rhythm as a whole to lengthen the duration, and shrink the
representations as a whole to decrease the playback duration of the rhythm. These approaches
allow them to approach analysis from the whole towards the parts (from each of the Core Four
representations), the parts (by interacting with the beats individually), or both the whole and
the part at the same time (while tapping their rhythm, managing the).

The Sound of Fractions
91
During our study, several students repeatedly communicated GUSTATORY references
and experiences. These descriptions went beyond typical word problems and highlighted that
the students had experience with making food, challenges with different situations when
dealing with food, and had a strong interest in food like they do in music. Taste, a somewhat
subjective sense, made it difficult to pose questions during the study that students could
answer accurately in relation to fractions, but recipes, and
Olfactory: Given the we have identified four of the other contexts as they relate to the
five senses, we briefly identified other representations that exist in the context relating to
smell. Smell (more so than taste) is very subjective, and lends itself as to a reason why we were
not able to identify many representations or performances in this context, or find research that
highlights bridging mathematics education with smell.
We arrange these contexts in Figure 12-2 to highlight the additional contexts that exist
infraction learning. This arrangement IS NOT meant to codify the all components of what it
means to understand the system of fractions, highlight one fraction scheme over another, or a
canonical list of the methods and skills required to perform fractions. It is also not to be
construed as a comprehensive or codified hierarchal relationship of the contexts that exist
cognitively or in the mathematical education area. Contexts are organized within the cognitive
domain (because we know and experience each of these contexts) from what is strongly
represented in the math domain, followed by our contribution of aural and physical, and the
other two sense which are yet to be discussed in detail in the academic community as having a
link to math or fraction learning. We also do not intend to say that these contexts,
representations, or performances are completely isolated. We argue that this arrangement
highlights the key differences in the ways that students can come to understand fractions, and
need to be separated and given an identity to fully take advantage of the performances,
representations, and contexts that students find themselves participating in.
Just as a words `bouncy ball’ on a page is physical ink on a physical page, it can also be
seen visually, elicit the sound and feel of a bouncing ball, and be recalled cognitively with
common stages (dropping, bouncing, catching) during the bouncing of the ball. This example
highlights a person who has had more or stronger experiences with a bouncy ball. We hope to
also provide the same descriptions and experiences of fractions with students by allowing them
to experience and interact with fractions in more contexts than traditional approaches.
This figure IS a visual representation to highlight some common and compelling
representations in different contexts that students are exposed to and familiar with. We also
want to communicate that this figure helps academics understand the many different
performances that are available to manipulate those representations. The temporal context is
purposefully on the edge of the cognitive area, as there is an argument that temporal exists
both internally and externally of the brain, hence why it is tied to several of the other sensory
contexts in varying strengths.
We also acknowledge that the arrangement of entities in Figure 12-2 does have
problems. From the cognitive sciences field, our organization may conflict with current
understanding of the organization of the brain, and is not as simple as the five senses. Also, we
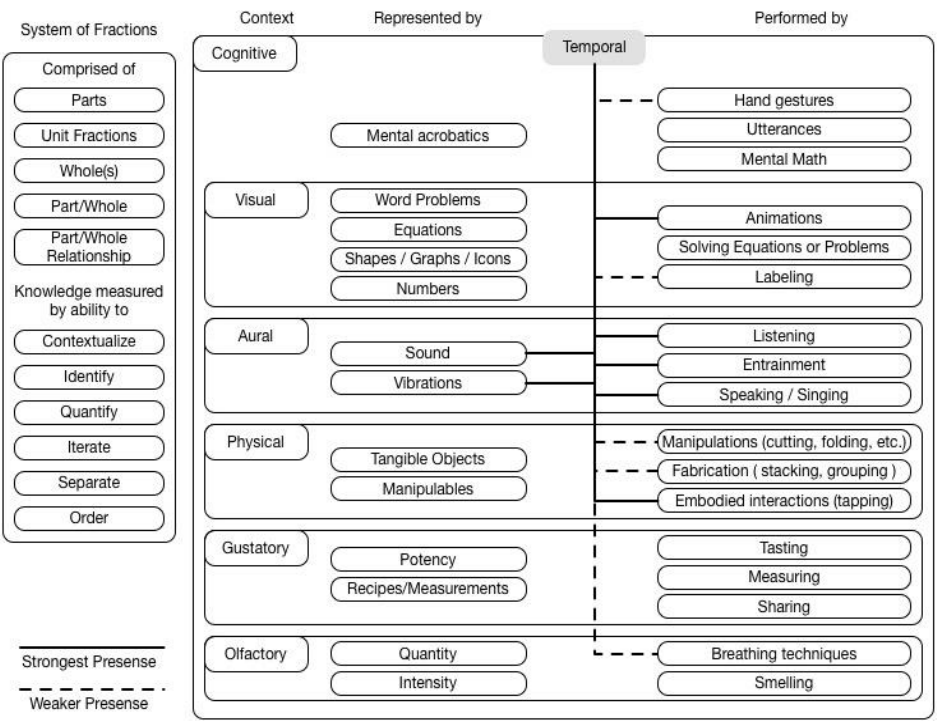
The Sound of Fractions
92
do not include additional physiological senses such as equilibrioception (sense of balance),
proprioception (sense of one’s own position), exteroception (sense of the world external to the
body), interoception (sense of the internal body), or kinesthesia (sense of one’s own
movement) that may be of interest in further evaluation, future work, or other literature.
Academics may argue that this representation is problematic and does not properly
represent their viewpoint. This argument highlights the justification to teach the same subject
in different contexts. As the experiences of students are expanded by the interactions with
varied representations, which are inherently abstract and possibly foreign, when considered
from another context or perspective, students become more skilled at identifying the important
components of the different representations to achieve a properly contextualized abstract idea.
Figure 12-2 By introducing a wholly different approach to fraction learning (particularly using
aural and embodied components) we noticed that other contexts exist to teach fractions with.
These were confirmed by students during the study, as well as other contexts were given as
examples by students (Gustatory) during discussion and interactions. This led us to consider how
math is represented in different contexts, their affordances and weaknesses, and what contexts
provide strong and meaningful learning opportunities with fewer misconceptions and difficulty
when learning fractions.
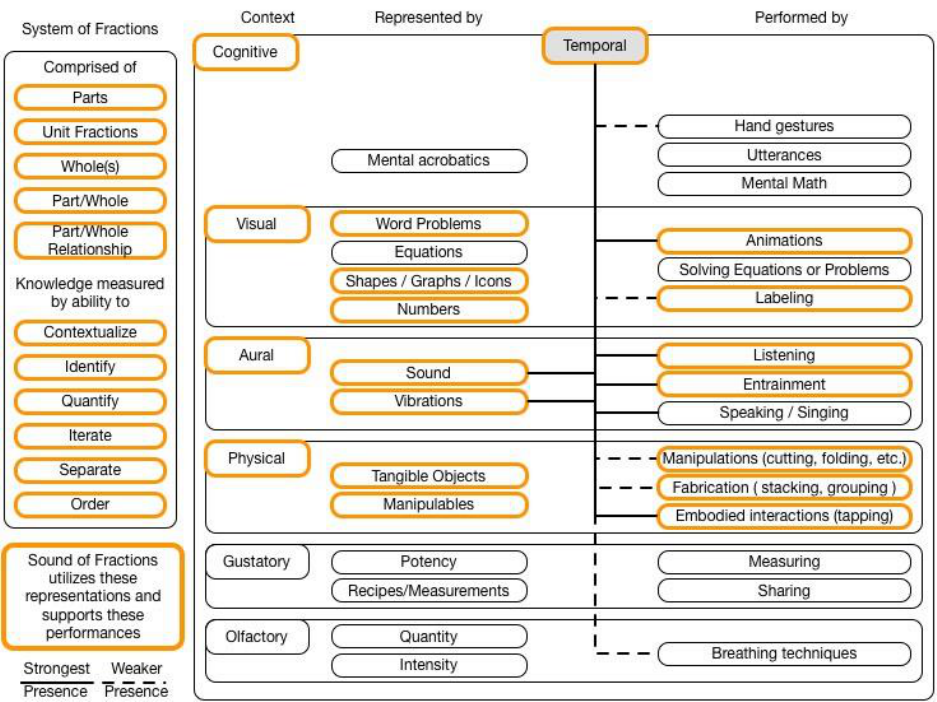
The Sound of Fractions
93
12.2.1.3 What SoF Supports
With a better understanding of what contexts exist in the math domain, currently,
perceived, and potentially in the future, we want to identify what components, measurements,
contexts, representations, and performances are supported by SoF.
Figure 12-3 The contexts, representations, and performances that SoF engages and challenges
students in, supports via the curriculum and socio-technical interface, and operates within a
dynamic environment to support different students’ approaches.
12.2.2 Fractions, Representations, and Abstraction
Fractions are inherently abstract. They describe the relationships between the part(s)
and a greater unit whole. Fractions exist in many forms (ratios and descriptions, pictures or
graphical elements, percentage, decimal, simple [numerator/denominator], mixed number,
complex) and the seminal way is hieroglyphic (Eves, 1969). The need for many representations
to describe the `same’ relationship is not by chance. Each representation highlights special
cases that exist when describing parts and wholes. For example, mixed numbers and improper
fractions deal with multiple unit wholes, ratios and descriptions focus on the relationship(s)
rather than the quantity of the part(s), percentages imply 100 equal units, and decimals adhere
The Sound of Fractions
94
to powers of ten. The hieroglyphic representations even take the form of adding unit fractions
of canonical [mostly unit] rational fractions to achieve non unit fractions.
Given the ability and need for us to describe the same relationship in different forms
requires a person to be able to understand each of the contexts in which one representational
form is affords benefits better than another. This requires both experience in different
contexts as well as an ability to think abstractly. Simply having experience in multiple domains
or contexts itself is not enough, as evidenced by the students who experience fractions in their
everyday lives and self reportedly understand their importance, but fail to identify the
important components in the various contexts or apply their knowledge correctly. Also, the
skill of thinking abstractly does not come without experiencing multiple situations and being
able to correctly identify and link the similarities and differences that exist in both contexts as
well as differentiating across contexts. This skill is also a major hurdle for students, as they may
not see the benefits of different fractional representations as they may not be properly situated
to see the strengths and weaknesses of particular representations.
Our approach of using a wholly separate context of aural and embodied interactions
with stronger temporal requirements forces provides more facets of the situation to identify
and develop abstract reasoning about fractions and the varying forms and requirements in
separate situations. Allowing the students to create their own representations also allows the
students to communicate with their peers and discover what features are important to include
when trying to convey their rhythm in an environment with shared goals. Moving beyond their
own artwork, students are introduced to our novel bead representation and can begin to apply
their knowledge from their own artwork. Taking another step, we provide animations to help
solidify the correct associations of what is conserved across representations, what features are
important, what is lost when moving between representations, and what representations elicit
stronger characteristics as they relate to fractions and the various forms fractions take. This
path of discovery, introduction, and guidance help students not only experience the embodied
and entrained characteristics of rhythms, but also helps them develop skills to correctly
perceive relationships between objects and scenarios in abstract ways.
12.3 Research Question 2: Can students who struggle with fractions make
meaningful progress in their composition, comprehension, and
communication when approaching the system of fractions from
perspectives related to music?
With a formidable approach to a new learning environment, we need to gauge what
works, what doesn’t, and how can this approach provide skills that can be used beyond
fractions and in other domains.
12.3.1 Hurdles Present in Students’ Misconceptions
Our curriculum is designed to start at a common shared interest for all students, and
progress in scaffolded discussion that utilizes the advantageous properties, representations and
The Sound of Fractions
95
embodied musical performances. This has proved to be great for ongoing engagement,
interest, and consideration. We struggle like many educators with helping those that are
struggling with concepts that are well below our curriculum’s expectations. Since we had not
formally tested our curriculum in a longer and more formal setting, we were surprised when we
came across certain clear hurdles.
12.3.1.1 n/n is confusing when n>20
We discuss what is the same, what is different, and what is important; A theme that we
use repeatedly during the curriculum to ultimately hone the skills of students to identify what
important components are needed to properly contextualize their situation. Early on in Group 1
when discussing what the artwork that students made to represent their rhythm, many
students were able to cite differences between the representations, but it was increasingly
harder for students to identify what is the same between students’ artwork. Students also
tended to describe the beats (parts), and not the rhythm (the/as a whole). To help aid the
students see some similarities, in particular that each person made a [whole] rhythm, the
conversation was guided towards mathematical properties of the rhythms as expressed in the
artwork.
Most students are able to properly identify the placement of a numerator and a
denominator, but their explanations of what they are vary widely, with few extending beyond a
shallow explanation of the numerator being `how many you have’ and the denominator being
`how many there are [total]’. This exhibited itself when we were discussing rhythms with fewer
beats, and how would we represent a rhythm of just 1 beat. Ultimately the students settled on
describing it in a fraction form of `1/1’. However, their understanding of their chosen
representation as it relates to both math and other rhythms is where we were able to highlight
an interesting phenomenon.
Since students chose `1/1’, it was implied (by both students and instructor) that
students meant there was 1 beat (numerator) and there was only 1 beat in the rhythm
(denominator). All students in this group except one did not explicitly represent rests, so the
majority of the rhythms (shared on the whiteboard in front of the classroom) ‘fit’ into this
description of having n/n beats. Our hope was to use the pose a situation that highlighted that
each rhythm is a whole, and that no matter how many beats there are, as long as they are all
sounding and equal, then the rhythm is whole. This could be expressed and verified through
the reflexive and symmetrical mathematical properties of their rhythms, that 1 is 1, 1/1 is the
same as 1, 1/1 is the same as 2/2, is the same as 10/10, is then same as n/n. However, when
increasing n, students were not as quick to respond that 10/10 is 1, and became less confident
when presented with 21/21 and higher.
Knowing that the students are familiar with the rule of reduction (supported by other
activities) shows their exposure to current math education. Their hesitance as n grows shows
that they lack a true understanding of what n/n really means, because they likely were only
exposed to n/n when n was 10 or less and memorized that rule, not understanding that it can
be extended to or abstractly thought of as a whole.

The Sound of Fractions
96
12.3.2 Reducing Complexity
Students acknowledge many times, in many of our data forms, that they know
understanding fractions is important for them and their future. They also acknowledge in all
forms of our data that the subject is hard, something that they do not fully comprehend, and
not interesting.
To tackle the lack of interest, we started this study from an area that is of high interest
to them, music. This has many positives as we have discussed ( see 5.3 Math, Music, and in
Between, 6 Our Prior Work, and 12.2 Other Domains and Approaches. It also has many
challenges. As we all learn, there are several pedagogical tools and approaches that students
and teachers use to communicate ideas. Some tools include (certainly not limited to) examples
(in the form of oral, written, illustrative, and video), experiments (manipulables), literature
(online, handheld, and handouts), and experiences. Some approaches that teachers use are
providing comparisons, allegories, similes, and reducing complexity (as seen from the
instructor’s view of what the student knows, does not know, and is familiar and experienced
in),
When these tools and approaches initially fail, teachers will continue to try and
approach the cognitive area that the troubled student(s) is in. This can only go so far, as
classroom management limits a significant amount of direct and tailored education. This limits
the teacher’s attention and potential for making meaningful progress. The students, in
particular those that have low SES resources, have less skill and resources to apply their own
agency to manage their own meta-cognition to move towards the teacher’s approach and
`meet-in-the-middle’. This creates a huge impasse. Students are frustrated and unable to
explain why, and teachers continue to teach for the larger class and recommend additional
opportunities that are exterior of the classroom (tutoring, after-school, or additional homework
or activities) that students and their parent(s) may not be able to accommodate.
SoF challenges students to experience music first, and inquire about the properties that
can be expressed in the math domain. We start off our curriculum by allowing the students to
create their own rhythm ( see Figure 15-3 and Figure 15-4 ), and challenge them to create a
representation of that rhythm so that another can reproduce their rhythm from looking at their
representation, with little to no guidance at all. This is not an easy task. Most students
immediately are interrupting the instructor that they do not understand, despite being
prequalified that (a) it is challenging, (b) We will repeat the task many times and successfully
slower, and (c) will help the students separate the task into smaller blocks.
Despite initial misunderstandings of the task to create their own representation of their
rhythm, the students begin to make their own rhythms that were rather complex (in number of
beats, speed, bi-modal, wide range of beat sizes [small, medium, and long size/duration],
rhythm-less [not a perceivable synchronized rhythm or poly-rhythm], poly-rhythmic, or not
cyclical). When the students then try to analyze their rhythm to begin to make their own
representation, they hit a road block that is expressed in their face, their body, and their voice.
When they revisit the task at hand though, prior to the teacher suggesting alternatives, the
students self-regulate their initial preference for complexity to manage the creative micro-

The Sound of Fractions
97
world that they are exploring. They do this by making rhythms that are simpler (with less beats,
slower, and with a narrow range of beat lengths/sizes) so that they can understand how to
translate the features that they want into a foreign context.
This phenomena of self-regulated learning in a foreign context is of particular interest to
us. First, this is an example of them being able to self regulate. Students are able to do this in a
domain that they are not normally able to navigate by themselves. Second, we know that their
interest helps fuel their progress, as they would have been disengaged, their typical response to
challenging math education. Third, students can navigate a task in a domain they struggle with
by approaching it from a domain they can perform in. Fourth, students are able to make
representations that are meaningful, and they continuously ideate over their representations of
their musical domain to decide what is important to include and exclude in the problem domain
of math. This translation allows for a solid building block to begin other exercises in the
curriculum that require students to contextualize, identify, quantify, iterate, separate, and
order the components of percussive rhythms.
12.3.2.1 Go Speed Racer Go!
Students initially want to create rhythms that are fun, resulting in one that is more
complex in nature, with more beats, rests, divisions, tempo, and polyrhythms. This is evidenced
in 11.3.1 The distribution of rhythms made by students with a particular signature, 11.3.2 The
distribution of recorded rhythms by duration, 11.3.3 The comparison of rhythmic complexity
against the number of beats tapped, 11.3.4 The number of instruments used in each rhythm,
and 11.3.7 Speeding Up versus Slowing Down. But what is also relevant is that students can’t
always operate in the complex musical world when asked mathematical questions, especially as
the questions become complex, nuanced, and particular. However, students are able to reduce
the complexity of their rhythms to a level that still elicits the mathematical question at hand,
and approach the mathematical question from a musical perspective. This helps solidify that
our approach is appropriate, culturally relevant, mathematically meaningful, and relevant for
learning. It is also important to not that the students themselves regulate the rhythms they
tap before the teacher instructs them to do so, showing they have agency within their own
learning environment, as well as the appropriate skills to navigate towards meaning with less
pedantic or demeaning instructions.
12.3.3 What is the numerator?
During our redesign of the interface and curriculum, we came to the decision to limit
the interface to initially only support one manipulable whole unit per instrument (this may be
thought of as a `measure’ in a musical domain), and not support additional measurements to
help teach more advanced concepts that surround mixed numbers. This decision was
supported by technical limitations, limitations in scheduling school and student participants for
the study, and being beyond the scope of a strong initial study. With a design that does not
fluidly undergird multiple manipulables in the same manner as the rest of the mathematical
concepts we support, we were surprised to find that students still operated with less
confidence when considering the size of the unit.

The Sound of Fractions
98
When transferring rhythms that students create to representations that they
themselves create, or when SoF does it for them when they record their rhythm, the concept of
a rest is not the forefront in the representation. For the representations that the students
made, only two included explicit rests. All the others represented the size (often related to
intensity) of the beat by the space between the items representing the beats. In the
representations that SoF creates, rests are in greyscale with lower opacity. While both choices
seem to align in their visual representations, this posed a problem for students, one that
challenges how to represent multiple beats of varying size in the same rhythm.
Some students tried to rearrange graphical beats so that they were closer to each other,
leaving a larger non uniform space between beats, as to give the beat the appearance
(graphical and aural) of being larger and louder. In representations in SoF that highlight division
(the bead and the line), the graphical beat does not change size, only location, reinforcing the
idea that the beat remains the same size in relation to all of its beats, the same way that the
representations that highlight duration (Pie and Bar) have graphical beats that change size
uniformly and immediately when a beat is added to or removed from the rhythm. This calls
attention to the lack of understanding from students to recognize the true size of a unit. The
students struggle to understand initially that a bead and a line (mark) remain constant graphical
sizes (diameter in relation to circumference and height in relation to width respectively) with
relative equal unit distance between regardless of the size (or duration) of a whole (rhythm).
12.3.3.1 What happens to the size and fraction of the numerator as the whole changes?
To help work through describing an individual beat’s size, we illustrated their sounding
aloud descriptions on the white board. The students chose to focus on the bead and the pie
representations. Prior to using SoF, students were challenged in an activity to describe what a
representation (both parts and whole) of a rhythm (beats and rhythm respectively) looks like
after it is doubled in size. Group 1’s descriptions were sufficient enough to draw a pie
representation that, according to their descriptions, included 11 pie slices arranged around the
circle with the same distance as it was previously. This led to a pie representation that only
accounted for one half of the whole circle, as seen in Figure 12-4. When the students then
were questioned about the remaining half, they were able to work through discussions that
they had to separate the actual size of the pie slice from the relationship to its whole.
Understanding that there are numerous ways to describe a beat was a pivotal point in their
understanding of fractions, and supported by the affordance of SoF with regards to supplying
multiple representation types that are manipulable as a whole. This learning moment was
supported when it came time to draw the bead representation twice the size of a previous
representation, where students both correctly identified the order and placement of the beats,
but also correctly and confidently described the size and fraction of each beat with relation to
each other and the whole rhythm.

The Sound of Fractions
99
Figure 12-4 The whiteboard showing the bead and the pie representations (chosen by the
students as preferable to work with) before and after doubling the size of them. The pie
representation previously (shown in the bottom right) was divided into 11 equal parts, but only
occupying 50% of the doubled circle. The number of iterated parts (made by the students)
equaled the smaller circle, but the design was starkly different and required reworking to ensure
that the unit fraction remained the same after the whole (rhythm) was doubled (in duration).
When performing the same activity with SoF and manipulating the representations,
students were accurately able to stretch the representations to become twice as large and
describe the position and size of the beats in both circular and linear representations.
12.3.3.2 Which comes first?
Students descriptions of order were correct, but to ensure that they were not just
guessing (given the the third remains the third when manipulating the size of the whole), we
posed questions about which beat will come first when comparing two different rhythms. In
Group 1 we asked if the second beat of three comes before the second beat of four, and for
Group 2 we asked if the second beat of two comes before the second beat of three. Both
groups had students that incorrectly thought the beat further (larger) along the rhythm came
before the former beat (smaller).
When questioned, the students who hypothesized incorrectly gave answers that were
related to its position on the circle. While their statements were correct (“one is loser to the
bottom than the other” and “the one with three is closer to the right than the one with the
two”) they are not pointing toward the ordered and scalar attributes that we want them to see.
Their answers hint that they have competing understanding of which beat is first in the circular
Bead representations. Rhythms, especially those represented as a Bead, which has a strong
The Sound of Fractions
100
suggestion of a never-ending repeating cycle, are harder for students to identify the beginning
of a rhythm during inspection at any given point during playback other than the initial playback,
which must include aural feedback, visual feedback, or both. This phenomenon is confirmed
form the beginning of the study when listening to rhythms of Taylor Swift (Shake it Off) and
Queen (We Will Rock You), which both were looped indefinitely, and students chose different
starting points, forgetting what the first sound was when the music started playing.
This does not mean that the students are unable to identify it the correct answer, only
that they are not yet confident in their answers in the situation when they have [circular]
representations that conflict with their understanding of fractions and their experience of the
rhythm. To help them confirm or change their answer, we allowed discussion and to add an
accompanying Line representation. This greatly helped the students to see the more
important attributes when comparing the unit fractions, size and order (by placement). This is
because the linear representations have more clear start (left most mark) and end (the
rightmost part of the rightmost beat) positions that the students can use to consider the
quantity (by size) and order, by both position. The line also helps students map events
temporally. After adding the line representation, students were able to more accurately
provide reasons as to why the smaller units with larger denominators come before the larger
units with smaller denominators. They provided descriptions similar to “it depends on where
the beat is on the line [or circle]”.
Upon playing the rhythm in SoF, students were undeniable as to which one was first.
This is an excellent case of how SoF provides a way for students hypothesize about math
related questions that they are not as confident in, and to identify the core concepts when both
the embodied, aural, temporal, and visual representations are share a uniform, proximal,
synchronized, and meaningful performance.
12.3.4 What is the denominator?
Another major component of fractions is the denominator and what it represents. A
denominator is more complex than just saying how many parts there are. It helps explain what
parts to consider, what parts to ignore, that the parts are all equal, how big the the whole is (by
virtue of how big the part(s) are), and how big each part is (by virtue of how big the whole is).
Our study helped understand a consistent phenomenon that exists when using embodied
rhythmic performances to approach math, that students tend to look identify some parts (beats
that make sound) more often than all parts (beats and rests that do not make sound).
Throughout the activities in both groups, students were asked to describe the rhythms
(whether they were created by SoF or the student’s themselves). The portion of their
descriptions that dealt with identifying how many parts there were were predominantly one
sided towards describing how many parts were beats (made sound and had full opacity color).
We had to consistently ask again (sometimes more than twice) for students to consider the
entire rhythm and all of its parts, including those parts that are ‘turned off’. Students are
categorizing the parts based on their state.

The Sound of Fractions
101
Most questions we ask students challenge them to describe their rhythms and
representations including all parts (beats and rests). Even basic descriptions allow the students
to delve further into more complex descriptions and relationships that help describe situations
in meaningful ways and communicate them more clearly. When students only focus on one
portion of the rhythm, they undermine their progress because they are failing to see the more
important complete larger whole. Problems posed to students in textbooks are often also
focused on a limited scope, asking how many apples in the basket of fruit. When you
understand fractions properly a person can identify what is important and what is not, but
when the student is confused as to what to consider, it is more difficult for them to answer a
question that asks you to answer questions that seemingly only focus on one portion. SoF
helps counteract this by enforcing unit fraction rhythms, providing a labeling mechanism for the
entire rhythm, constant inclusion of both beats and rests (two inherent properties in non-
metronomic rhythms), allowing the state of the beat to be binary, and providing aural feedback
for verification.
12.3.5 What is a fraction?
Students entered into our study with their own preconceived notion of what a fraction
is and their own experiences with the system of fractions. They also already were already
familiar with music and have skills related to making music and rhythms. As noted in 10.5.1 Pre-
post Test – What are fractions, after students participated in our study, they were able to
provide more descriptions than before, descriptions that are more robust, and highlight new
abstract thinking in contexts they previously had not explored. It is also important to look at
how the students were able to map the musical and math patterns to each other.
12.3.5.1 pattern.map(function(Music||Math){ return Music ? Math : Music })
When students are asked to make a rhythm, whether it is reiterated to be repetitive or
not, they always made one rhythm, and did not repeat it. We propose this is for many reasons.
First, students are concentrating on the performing the physical actions of their internal
rhythm, and managing that performance feedback loop as tapping persists within the rhythm.
This highlights their creative skills and abilities, and their interest in music with regards to
perceiving, creating, performing, and entraining patterns. Second, students are trying to
concentrate on the [curricular] task at hand, and therefore pause after each performance to
evaluate if their rhythm and performance achieve the goal. This shows that students are able
to analyze, mimic, repeat, and critique patterns. Thirdly, students adjust their rhythms over
time. They do this to experiment and adjust towards a goal. These actions highlight students’
abilities to manipulate, enhance, perfect, and familiarize musical patterns.
Understanding the complexity of musical performances is important, especially as it
pertains to knowledge transfer across domains. In the mathematical domain, students also
share many of the skills related to patterns. Infants understand logarithmic change. Very
young children learn to count. Kindergarten aged students being to categorize and measure.
Younger primary education students begin to understand common units and manipulations.
Towards the end of primary education, students will work with higher order functions, ratios,

The Sound of Fractions
102
and applied approaches. As students progress in their academic careers, their skills for
contextualizing, identifying, creating, and manipulating patterns grow.
Both domains have skills that are challenging. This is confirmed by students disengaging
in either or both domains, in addition to displaying lower grades or performances. A
compelling strength of including both math and music is that students can draw upon
experiences, rules, representations, and vocabulary in one domain, and concretely map them to
the same in the other domain. We focus primarily on meaningful progression in the math
domain, to helps students understand the system of fractions, but we do so with experiences in
both domains. Helping students move between both domains helps students perform wholly
in a single domain better. This is analogous to language acquisition. Learning and performing
in a second language helps you in your native tongue.
With students actively participating in a structured curriculum supported by aural,
visual, and physical context that have strong embodied and temporal components, students
can develop stronger understandings in each domain, as well as more abstract reasoning to
apply their knowledge beyond the classroom setting. This is evidenced by students’
performances of music making in clearer subsequent performances coupled with their ability to
recognize and describe mathematical patterns.
12.3.5.2 Descriptions and Definitions of Fractions as they Relate to SoF
Students were asked throughout the study to explain what fractions mean to them,
what they are, identify the parts and whole(s), make representations of fractions, and apply
their understanding in different contexts. Student definitions are often initial terse, off-topic,
not comprehensive, and fail to identify important component or relationships about fractions
or the system that they describe. This is discussed in further detail in 10.5.1 Pre-post Test –
What are fractions. It is of no surprise that when tasked to make physical representations of
their aural rhythms so that others can replicate them, that students are able to provide rich
representations based on music (Upitis, 1993). It is also no surprise that students can make
complex rhythms as described in 12.3.2.1 Go Speed Racer Go!. What is interesting is the
explanations of fractions towards the end of the study, after incorporating SoF and the
accompanying curriculum.
But why are the mathematical definitions initially shorter and less complex initially, but
the musical representations (aural, embodied, and tangible) are not, and then the
mathematical definitions longer, stronger, and more meaningful to the students and also
mathematically? The short answer is that our approach is promising. Our reasoning is because:
Students can use their own creation and skills in one domain and with guided
instruction can identify the important components for a given context
Students who are exposed to and operate within richer environments experience and
provide richer descriptions
Representations and embodied interactions with targeted mathematical components
provide meaningful avenues to understand relationship and representational similarity

The Sound of Fractions
103
12.4 Research Question 3: How do multiple, novel, rich, and interactive
culturally appropriate representations affect engagement in a
learning environment?
With several examples of how our approach provides meaningful academic progress
and skills that enhance their problem solving skills, we need to evaluate the engagement of
students and the impact it has.
12.4.1 Hey Mikey, I think s/he likes it!
During our study we asked questions to determine what the students found fun,
interesting, motivating, and educational. Students repeatedly replied that they like listening to
and making music, making tangible representations, hearing and interacting with their rhythms,
seeing different representations and their similarities (see 15.5 Group 1 Video Data and Notes
15.6 Group 2 Video Data and Notes for occurrences). Students appreciated the examples tied to
music that they themselves created, individually or as a class group or class. They commented
positively on popular musical references. Students also rushed into the classroom with
excitement, even after returning from break. They also enjoyed making references learned in
class to other experiences outside of school.
12.4.2 Multiple Representations
Math has many representations, even before reaching fractions, and especially reaching
far beyond. They each have their purpose too. As with all representations, there is a trade off,
highlighting one feature and backgrounds another. Utilizing a single feature risks losing another
altogether. But creating, identifying, and manipulating each representation challenges people
to be engaged with the underlying principle(s) that the representations seek to represent. The
beauty of our approach is that the students operate within the educational environment first
without knowing the underlying ideas, concepts, and principles that we are trying to educate
them on. They simply have so many to work with that they are excited by the idea to choose,
an area of agency that is often overlooked in some settings. By providing students with
multiple representations and allowing them the opportunity to choose is a strong reason why
we are able to capture their attention in our curriculum.
12.4.3 Novel Representations
When we present the Bead representation, its novelty is challenging. Many of our
exercises focus on interacting with the Bead, but students also chose it when given the option
to work with any representation type. The Bead provides circular, repetitive, cyclical,
segmented, divisional, scalar, ordered, grouped, prototypical, colorful, interactive, shrink-able,
stretch-able, transition-able, manipulable, static, active, attractive, simple, and approachable
properties. Some of these attributes are conflicting, such as stretch-able and shrink-able, active
and static, and grouped and divisional. These juxtapositional properties, along with the others,
are carefully integrated into this single representation to allow contextual exploration of what a
The Sound of Fractions
104
fraction can describe. By providing multiple various activities for students to discover and
interact with these properties, the students are not only interested, but remain intrigued.
12.4.4 Rich [mathematically oriented and musically related] Representations
Just like the Bead representation, the other three of the Core Four provide
mathematically rich properties. SoF also helps provide musical representations that are
accessible to the students, who are interested in music. Students are able to hear and
recognize their rhythms that they record in SoF. This provides a sense of accomplishment and
successful communication to another, albeit themselves via the computer (especially since the
challenge of making tangible representations of their rhythms is quite complex, unguided, and
generally unreproducible when sharing with a classmate).
Students tendency to gravitate towards faster or more complex rhythms in non directed
situations also shows that we capture their attention. The complexity of their rhythms in
comparison to the activity at hand keeps their curiosity, and the scaffolding and structure of the
curriculum helps ensure that the mathematical idea is properly communicated. SoF and the
curriculum also provide mechanisms to consistently build upon and accurately hone their
descriptions of their rhythms and other representations in mathematical and fractional terms.
12.4.5 Transitions
‘Woah!.......’ This expression was observed many times and in many forms when
students discovered that the Core Fore could be graphically transitioned between each other.
This awesome XXXX cite citation needed eddy izzard XXXX property also provides many
computational thinking properties, such as abstraction, functions, and modeling. Its power of
making clearly defined one to one associations also lends its hand to describing non math
domain situations into standard mathematical representations, especially in conjunction with
our labeling mechanism. Given the Core Four can be transitioned between each other, SoF
provides twelve separate transitions alone that students can operate and study. It also
reinforces the idea that representations are not immutable.
12.4.6 Engagement as a whole
Engagement in the classroom is powerful. If you can capture a student’s interest,
curiosity, and perseverance consistently, then the learning environment and the topics being
discussed are engaging, meaningful, and rewarding (not just for the student). Students also
commented that they struggled with certain activities, but were able persevere with answers
and reasoning on their own given the proper amount of time to think and explore.
In short, students experienced excitement and engaging participation with SoF in a way
that made it possible for them to interact with math in an academically meaningful way they
had previously lost.

The Sound of Fractions
105
13 FUTURE WORK
We have shown that there is a great need to approach fraction learning from a musical,
embodied, and culturally relevant domain that students maintain interest, can perform
accurately in, and make meaningful academic progress. This study, while quite extensive, does
not provide for all domains or contexts thoroughly, and our research has shown that there is
strong potential for more progress.
13.1.1 Enhancements for additional studies
To enhance our analysis, we would like to study log data in more robust way, and need a
way to conceptualize and record data in a synchronized way across video and queryable data
structures.
13.1.2 Other Domains and Approaches
- Calculus before arithmetic. Include music?
- Mixed numbers, multiple measures, non unit fraction rhythms.
- Better scheduling, handouts, and a button to separate tasks for the database
- Random patterns of new representations, to prevent pushing a standard way of
representing
14 CONCLUSION
We focused on an important and challenging area of mathematics education where
many students fail to make meaningful progress, fractions. By focusing on the social and
economic backgrounds of the students who needed the most help, we developed a socio-
technical program with an accompanying curriculum to address the situation from the students’
perspective, and progressed using contexts familiar, approachable, performable, and
interesting to students. This robust approach showed promising results of learning while
providing an experience that highlights the whole and the parts at the same time in a culturally
relevant set of activities. These embodied activities were performed alongside our aural and
visual application that helped scaffold students’ knowledge to gradually bring students into
more standard mathematical representations and situations.
We have provided the history, a literature review, our motivations and prior work, and
the data for review. We ran the study and analyzed the data to discover new phenomena that
highlights future potential and possible areas of improvement. We look forward to continuing
this project as another tool for educators and motivated individuals to learn something new
and share with the community at large.
15 APPENDIX
15.1 Abbreviations
SoF – Sound of Fractions - our socio-technical application to help teach fractions
CC – Common Core – The United States based Kindergarden-12 curriculum
SOL – The Virginia state based Standards Of Learning Kindergarden-12 curriculum
SES – SocioEconomic Status
UI – User Interface
UX – User Experience
15.2 Accessibility of this Thesis Document
This thesis is available at http://www.specialorange.org/thesis in many formats with
accompanying slides, presentation, and links to data sources.
All figures should have alternate text for screen readers.
The colors of the document text are chosen to support color-blindness, and other colors in
figures. The figures of the interface are not designed to support color blindness. Please accept
our apology.

The Sound of Fractions
107
15.3 Blank Lesson Plan
Figure 15-1 : The Lesson Plan planning page. This allows researchers to identify the meaningful
components of a well designed lesson and communicate them easily for a teacher to review and
reference during a class session.

The Sound of Fractions
108
15.4 Curriculum
Figure 15-2 What do Fractions mean to you? - Lesson Plan Day 1, Activity 1

The Sound of Fractions
109
Figure 15-3 Listening to a Rhythm - Lesson Plan Day 1, Activity 2
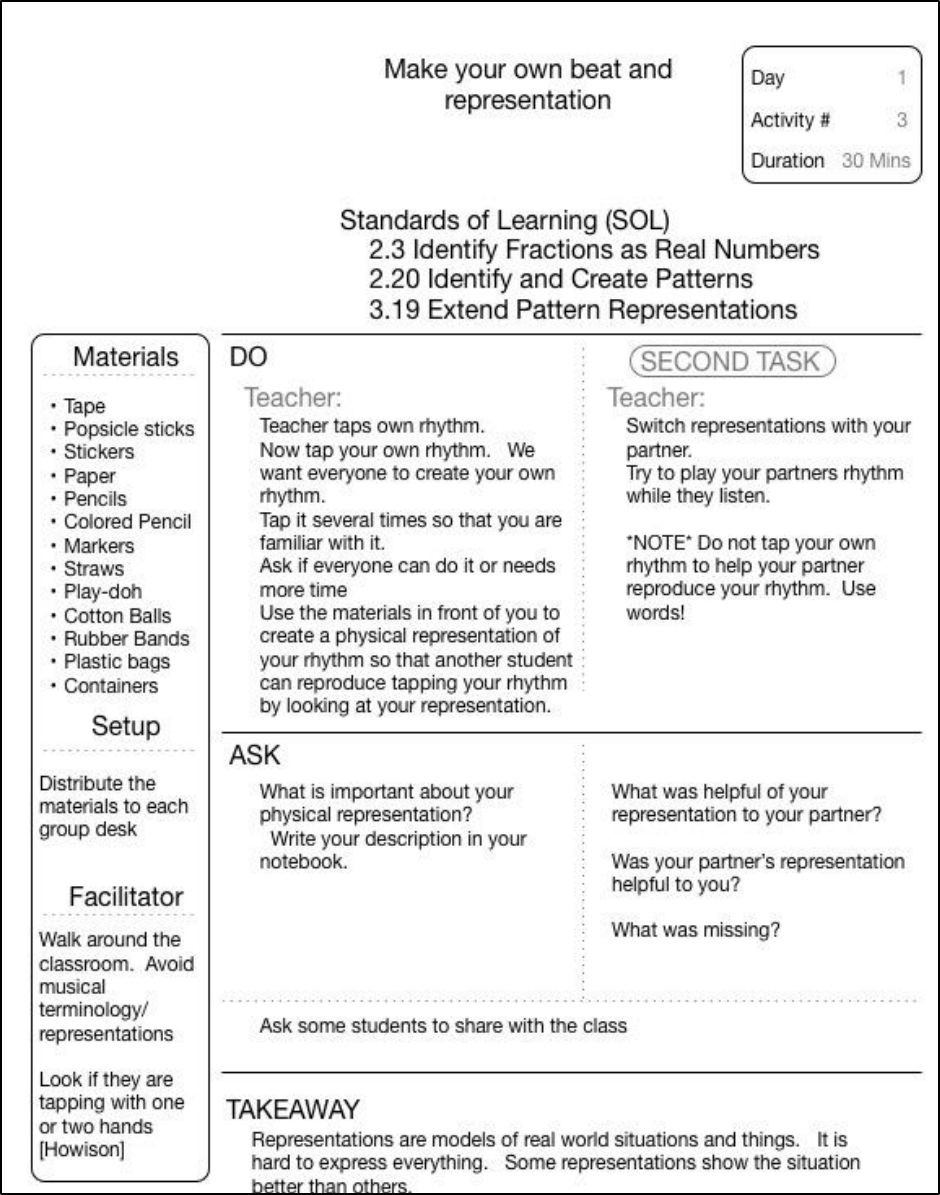
The Sound of Fractions
110
Figure 15-4 Make your own rhythm and representation - Lesson Plan Day 1, Activity 3

The Sound of Fractions
111
Figure 15-5 Make a new representation - Lesson Plan Day 1, Activity 4

The Sound of Fractions
112
Figure 15-6 Day 1 Homework Patterns - Lesson Plan Day 1, Homework

The Sound of Fractions
113
Figure 15-7 Describe What's important - Lesson Plan Day 2, Activity 1
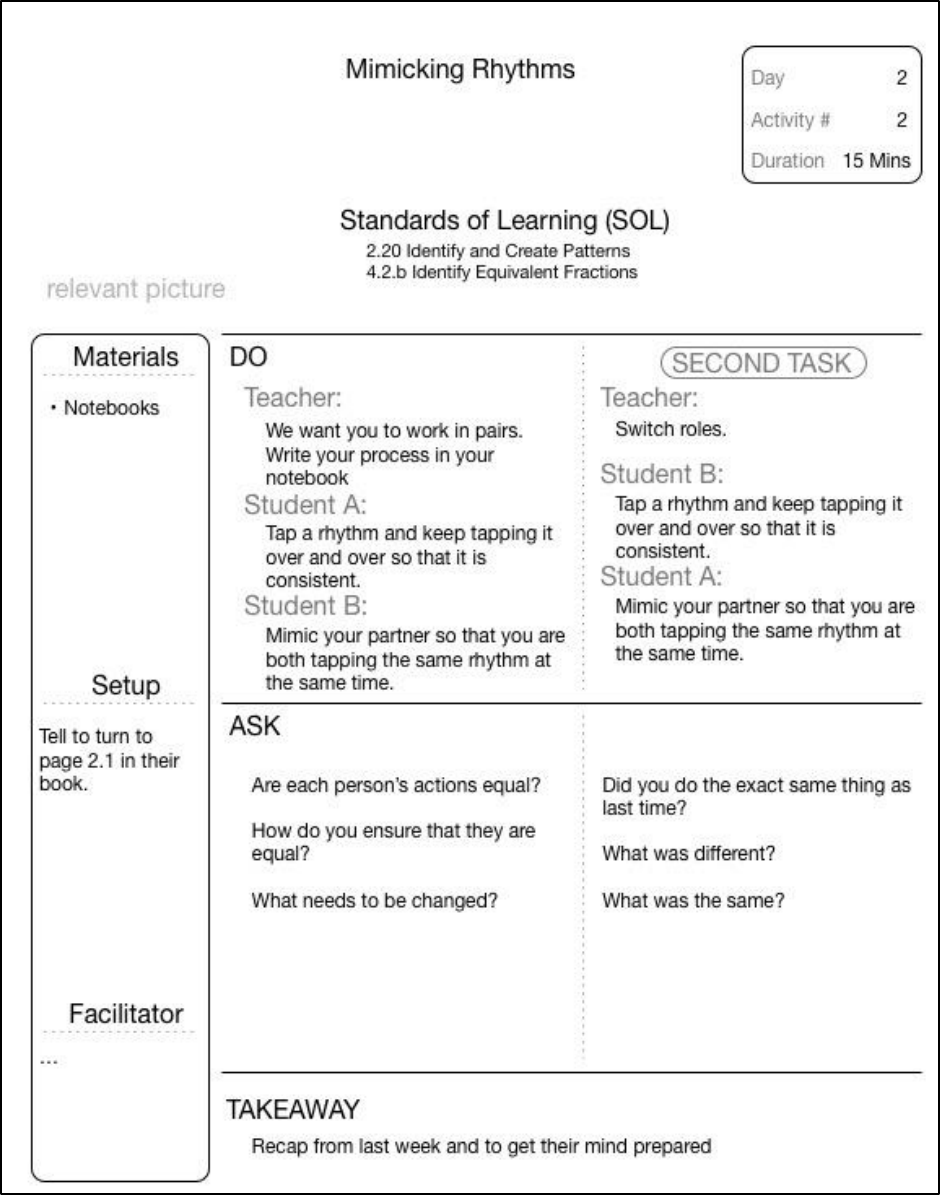
The Sound of Fractions
114
Figure 15-8 Mimicking Rhythms - Lesson Plan Day 2, Activity 2

The Sound of Fractions
115
Figure 15-9 What Size!? - Lesson Plan Day 2, Activity 3
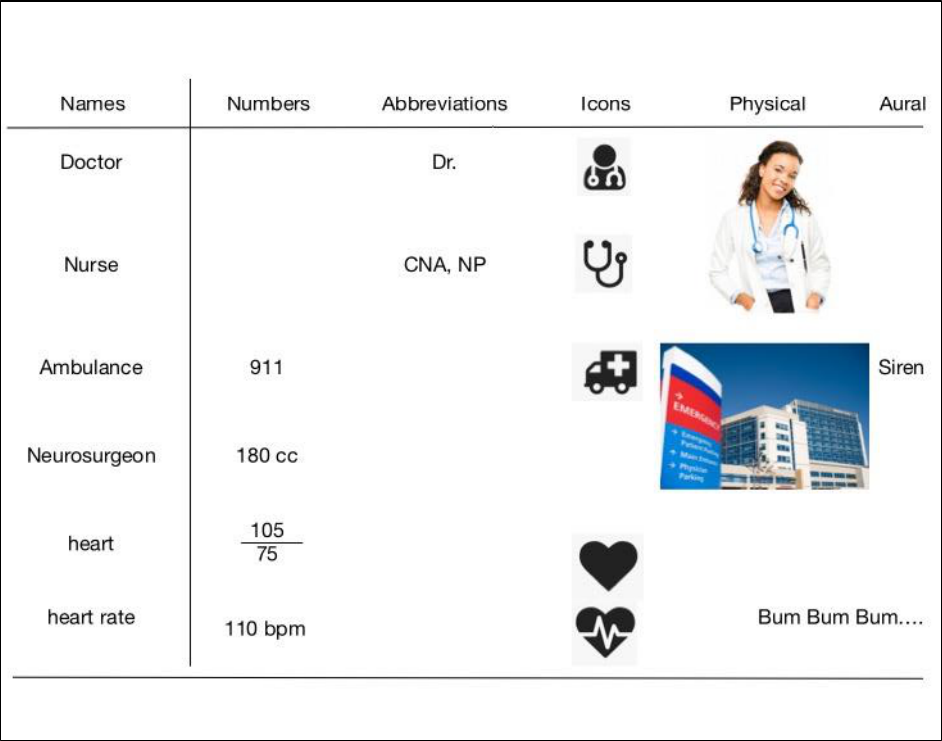
The Sound of Fractions
116
Figure 15-10 The Medical Representations Handout - Lesson Plan Day 2, Activity 3

The Sound of Fractions
117
Figure 15-11 Make your own fraction representation - Lesson Plan Day 2, Activity 4

The Sound of Fractions
118
Figure 15-12 The numbers representation handout - Lesson Plan Day 2, Activity 4

The Sound of Fractions
119
Figure 15-13 Play with SoF - Lesson Plan Day 2, Activity 5

The Sound of Fractions
120
Figure 15-14 Day 2 Homework

The Sound of Fractions
121
Figure 15-15 Make a Bead representation - Lesson Plan Day 3, Activity 1
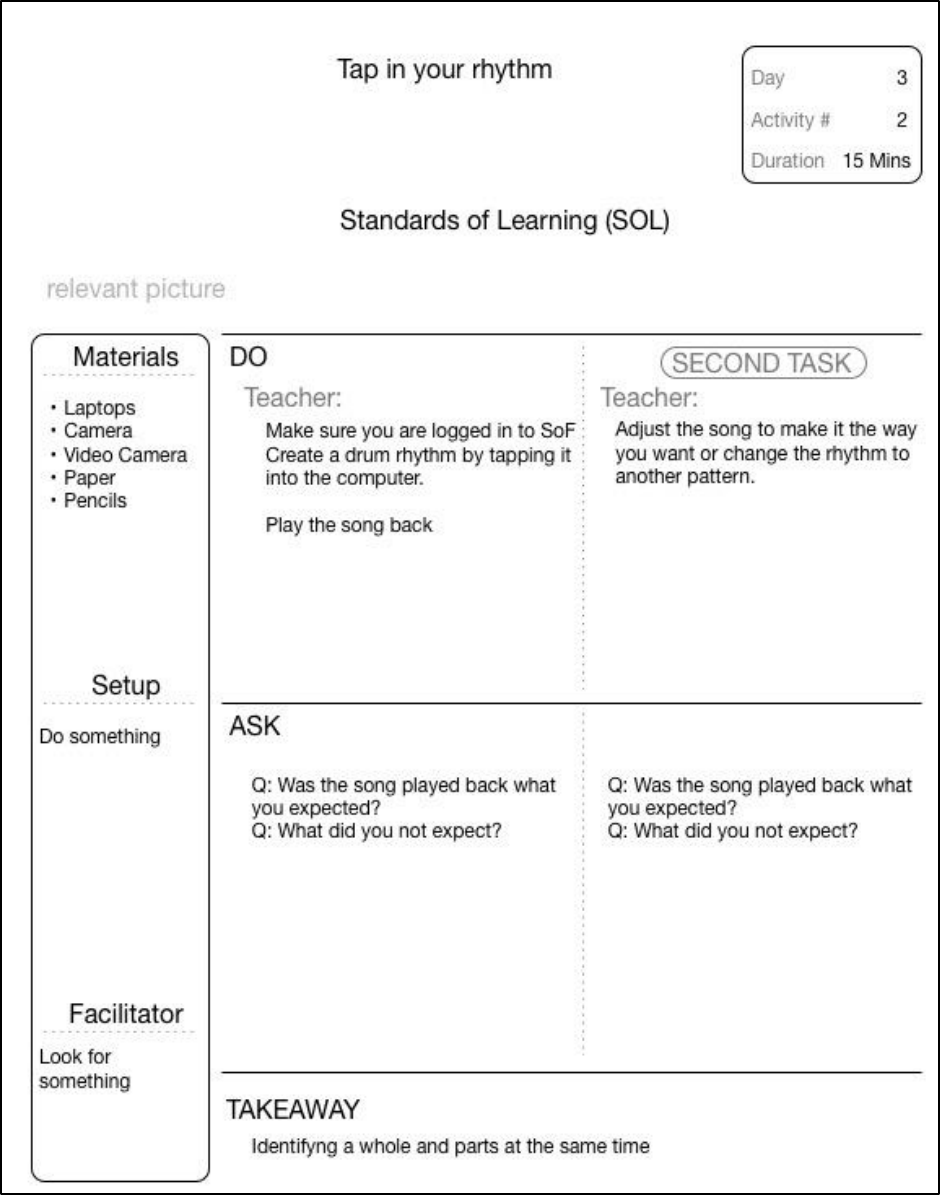
The Sound of Fractions
122
Figure 15-16 Tap in your rhythm - Lesson Plan Day 3, Activity 2

The Sound of Fractions
123
Figure 15-17 What is a whole - Lesson Plan Day 3, Activity 3

The Sound of Fractions
124
Figure 15-18 Day 3 Homework
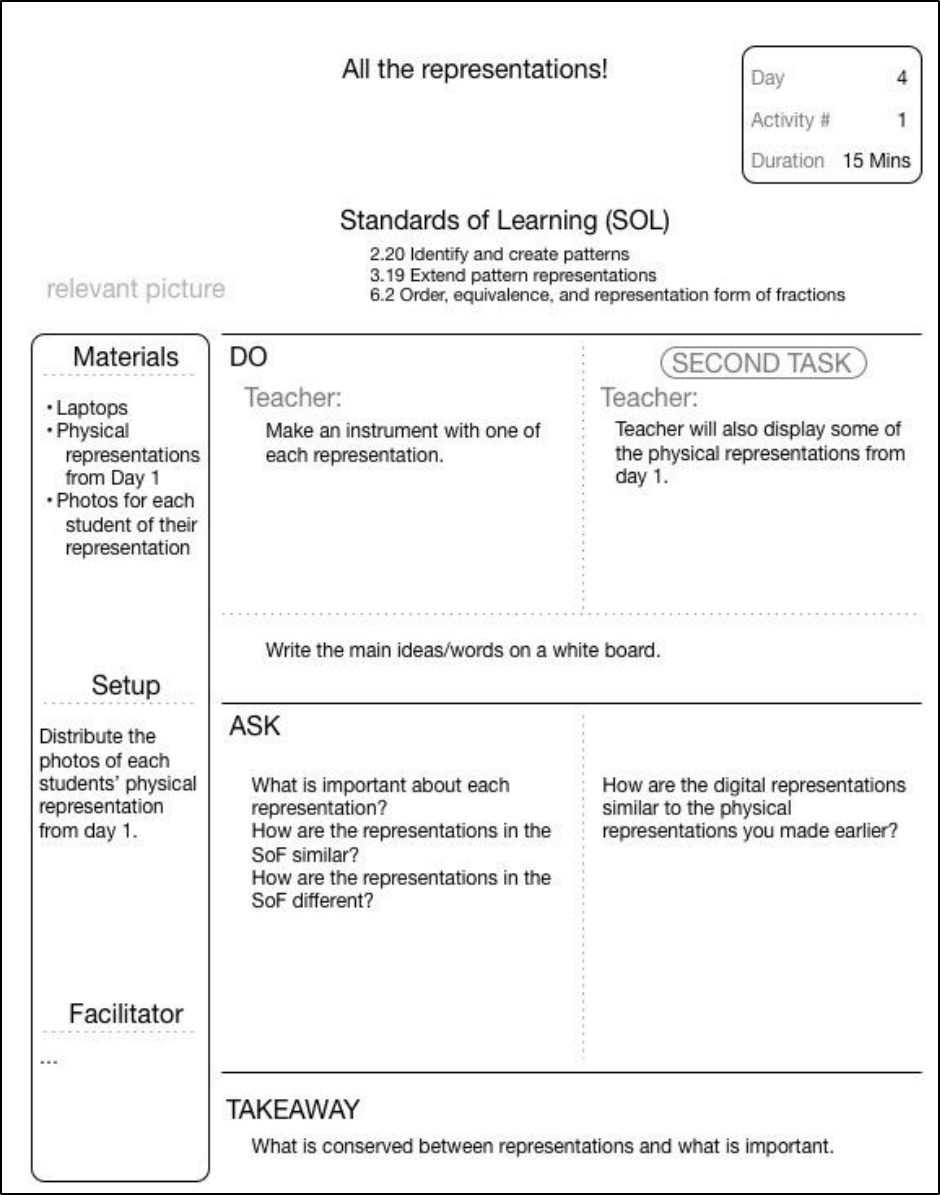
The Sound of Fractions
125
Figure 15-19 All the representations! - Lesson Plan Day 4, Activity 1
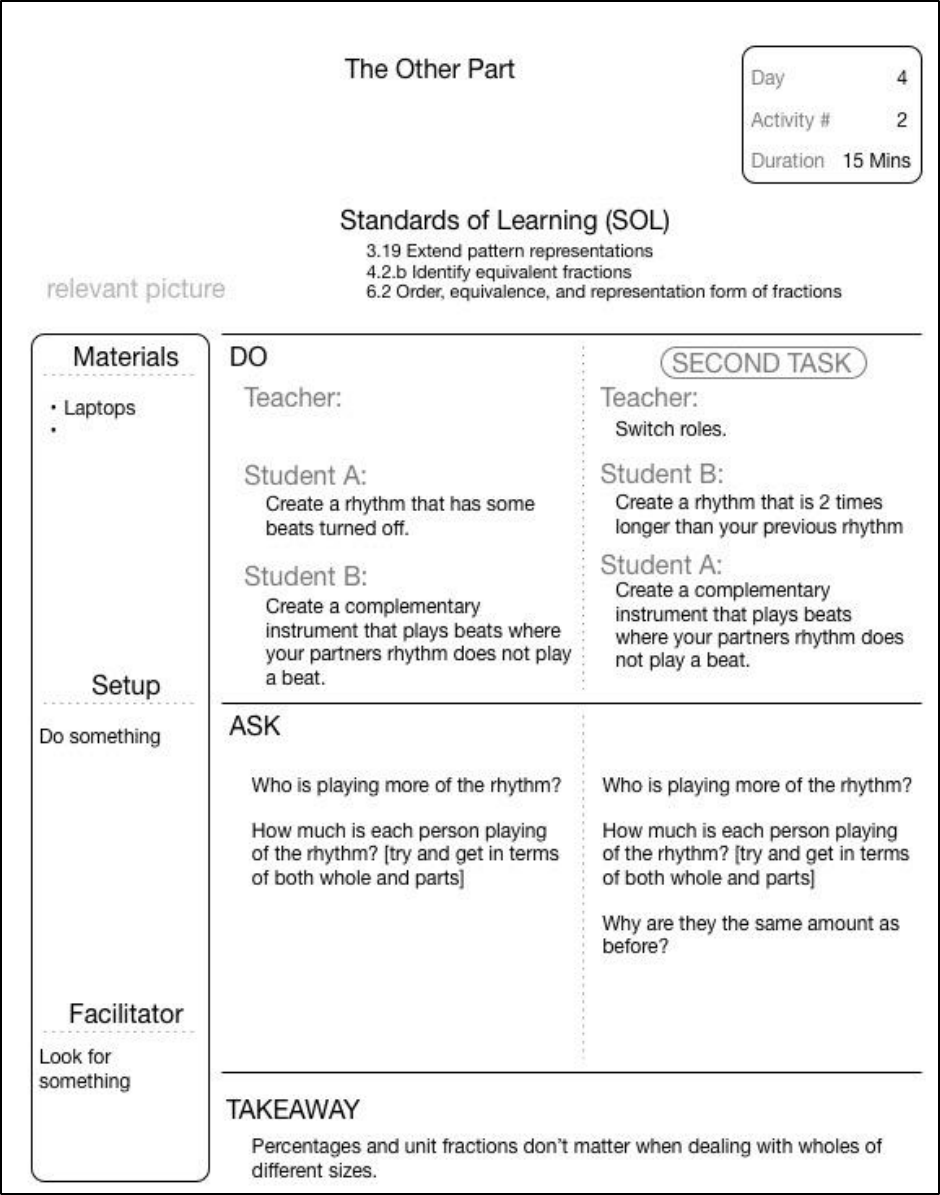
The Sound of Fractions
126
Figure 15-20 The Other Part - Lesson Plan Day 4, Activity 2

The Sound of Fractions
127
Figure 15-21 Which comes first? - Lesson Plan Day 4, Activity 3

The Sound of Fractions
128
Figure 15-22 Day 4 Homework

The Sound of Fractions
129
Figure 15-23 Recap - Lesson Plan Day 5, Activity 1
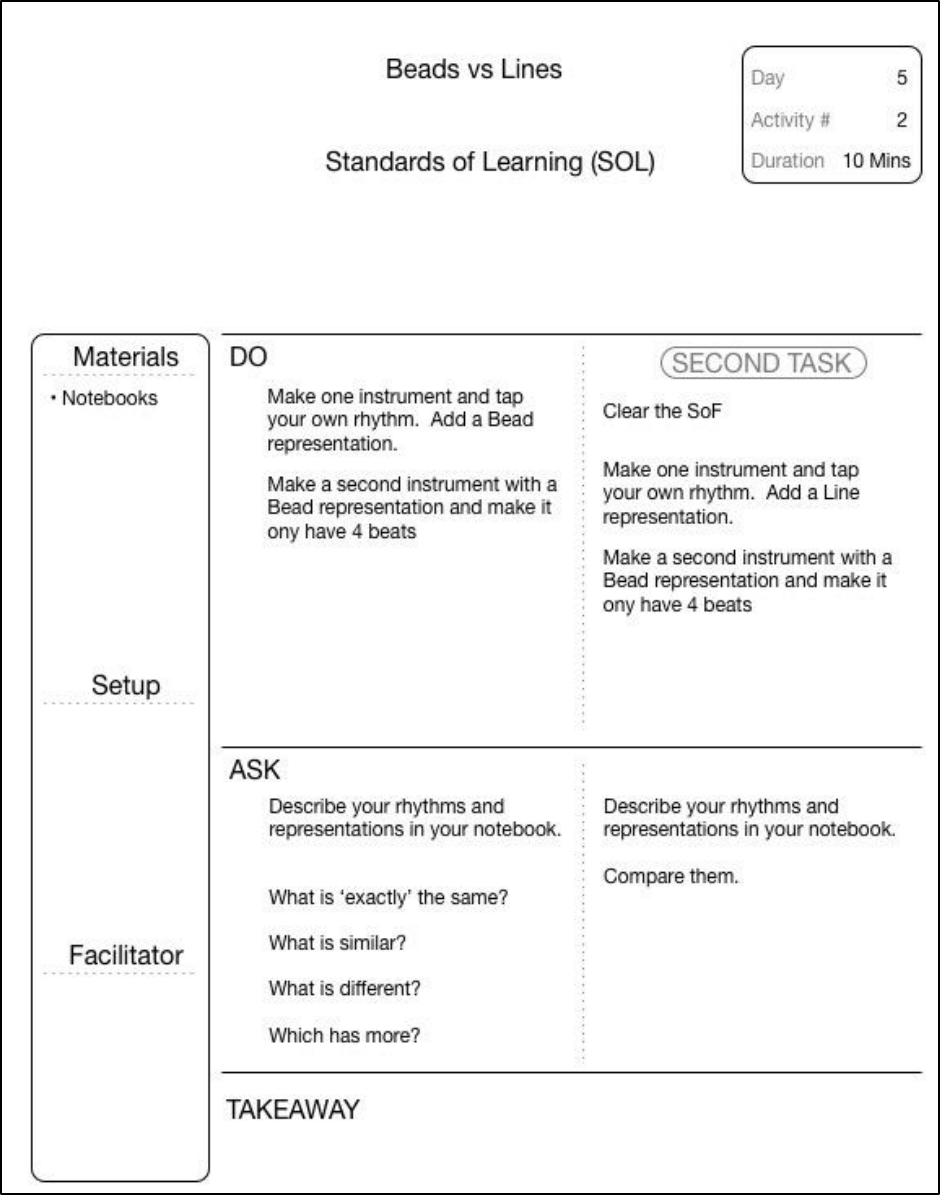
The Sound of Fractions
130
Figure 15-24 Beads vs Lines - Lesson Plan Day 5, Activity 2
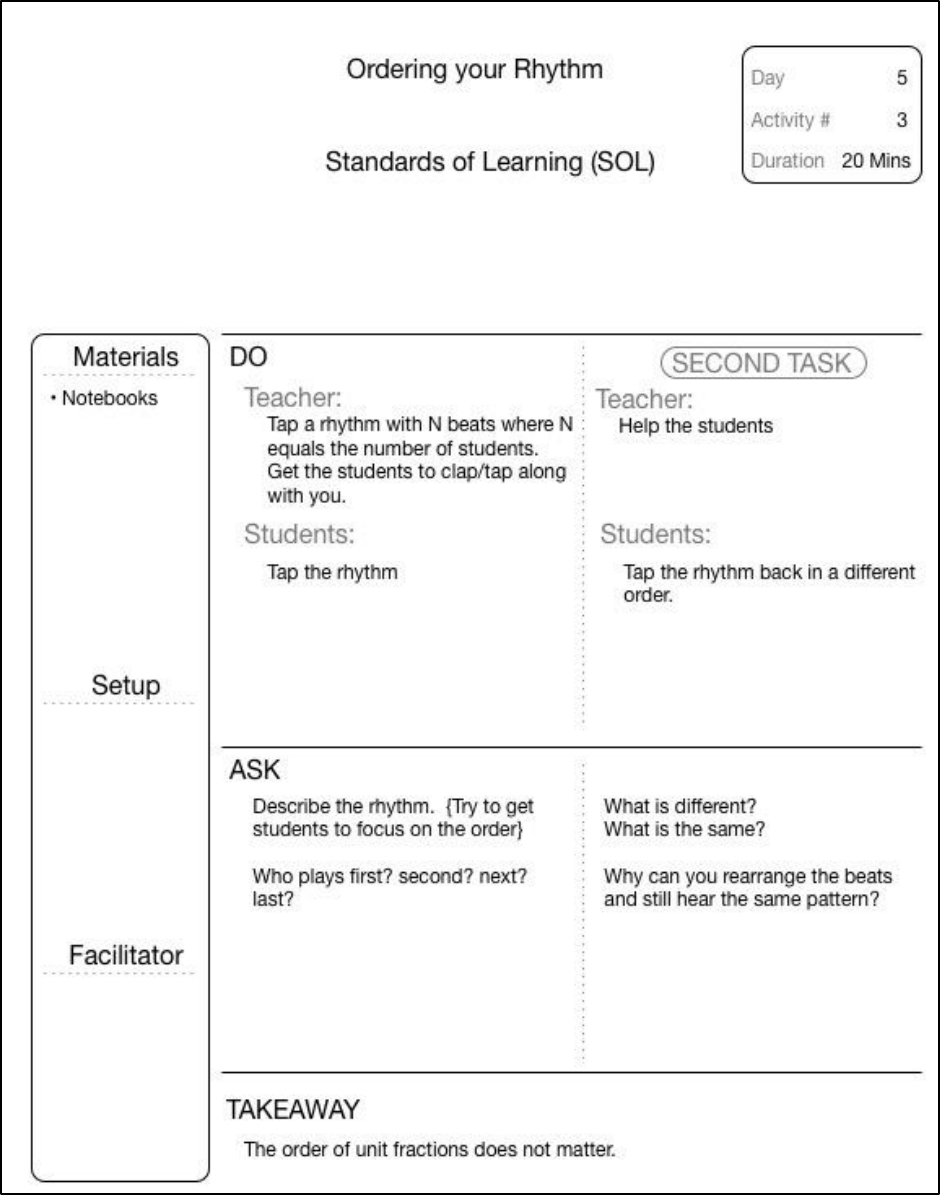
The Sound of Fractions
131
Figure 15-25 Ordering your rhythm - Lesson Plan Day 5, Activity 3
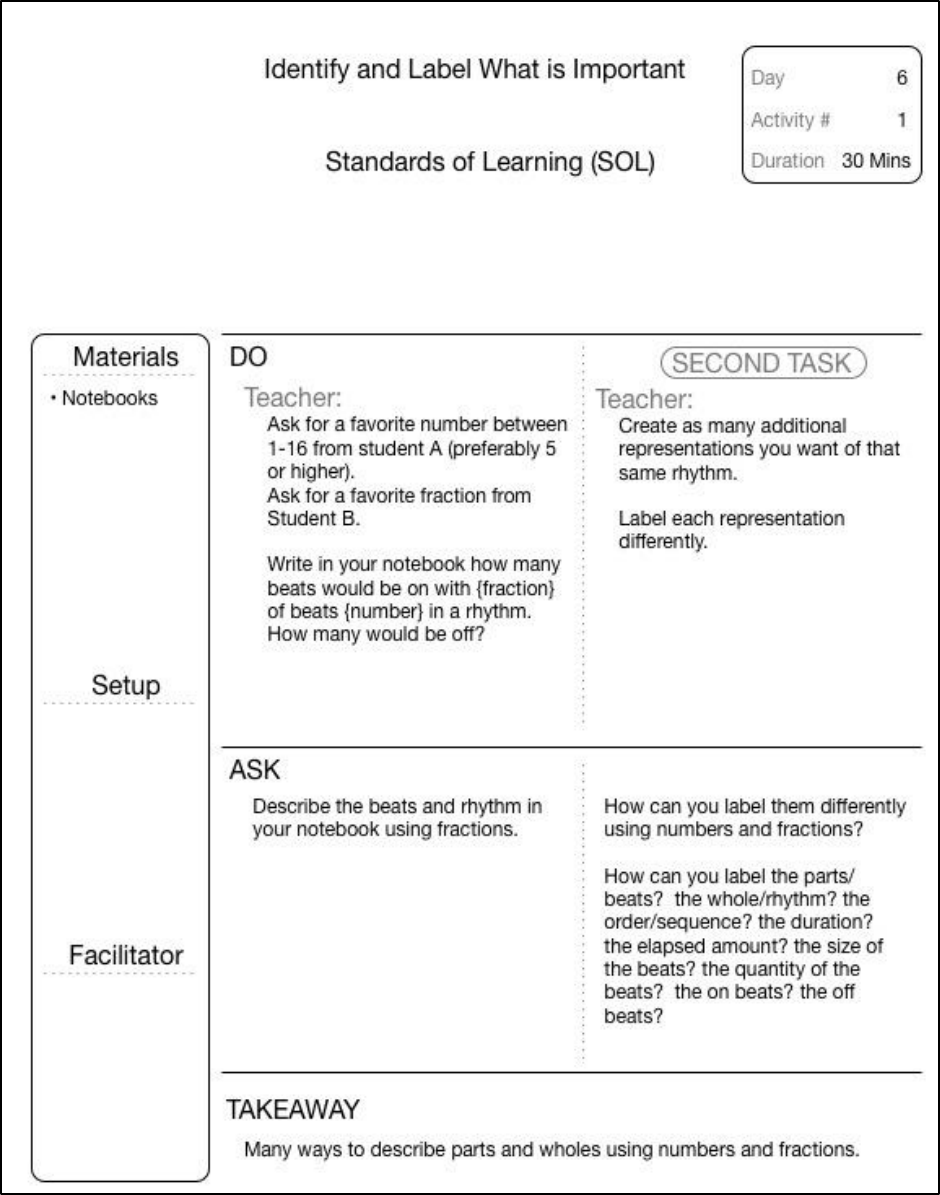
The Sound of Fractions
132
Figure 15-26 Identify and Label what is important - Lesson Plan Day 6, Activity 1

The Sound of Fractions
133
Figure 15-27 Transitioning to other representations - Lesson Plan Day 6, Activity 2
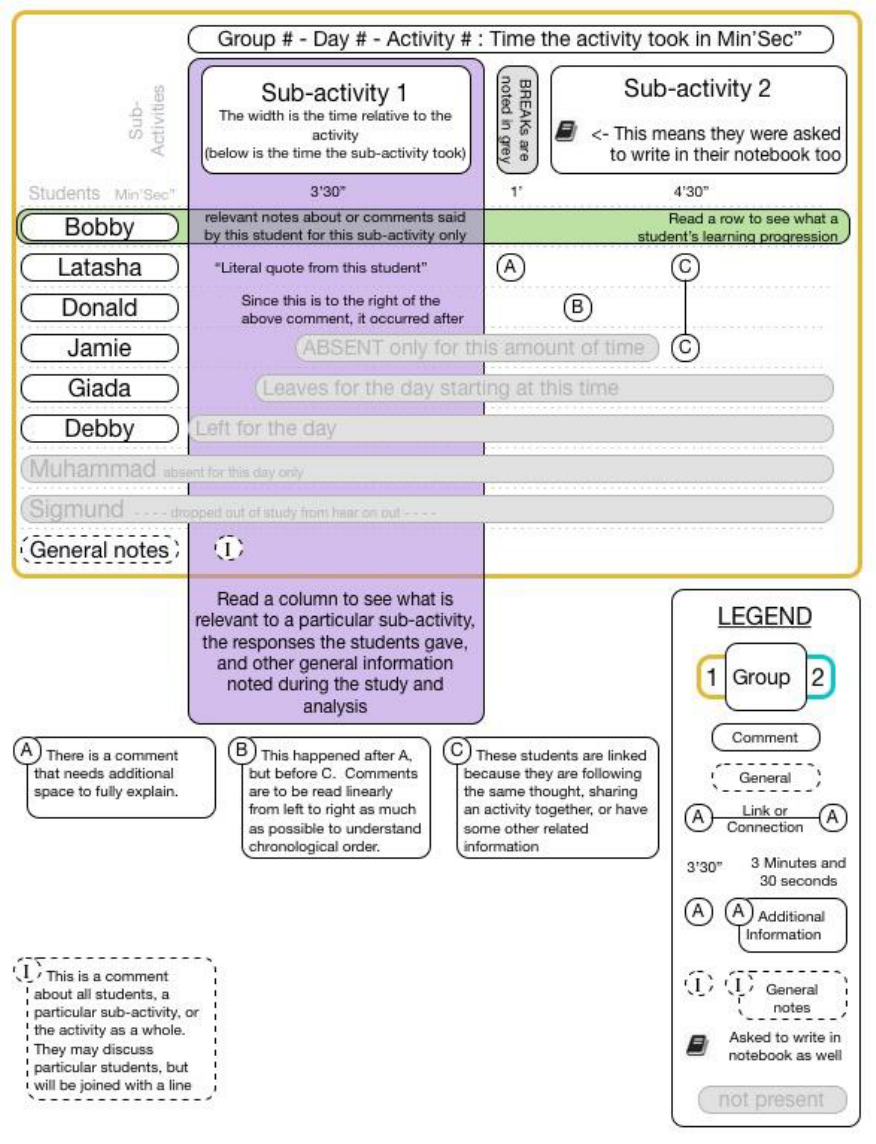
The Sound of Fractions
134
15.5 Group 1 Video Data and Notes
Figure 15-28 A Legend and description for reviewing video data of activities and sub-activities
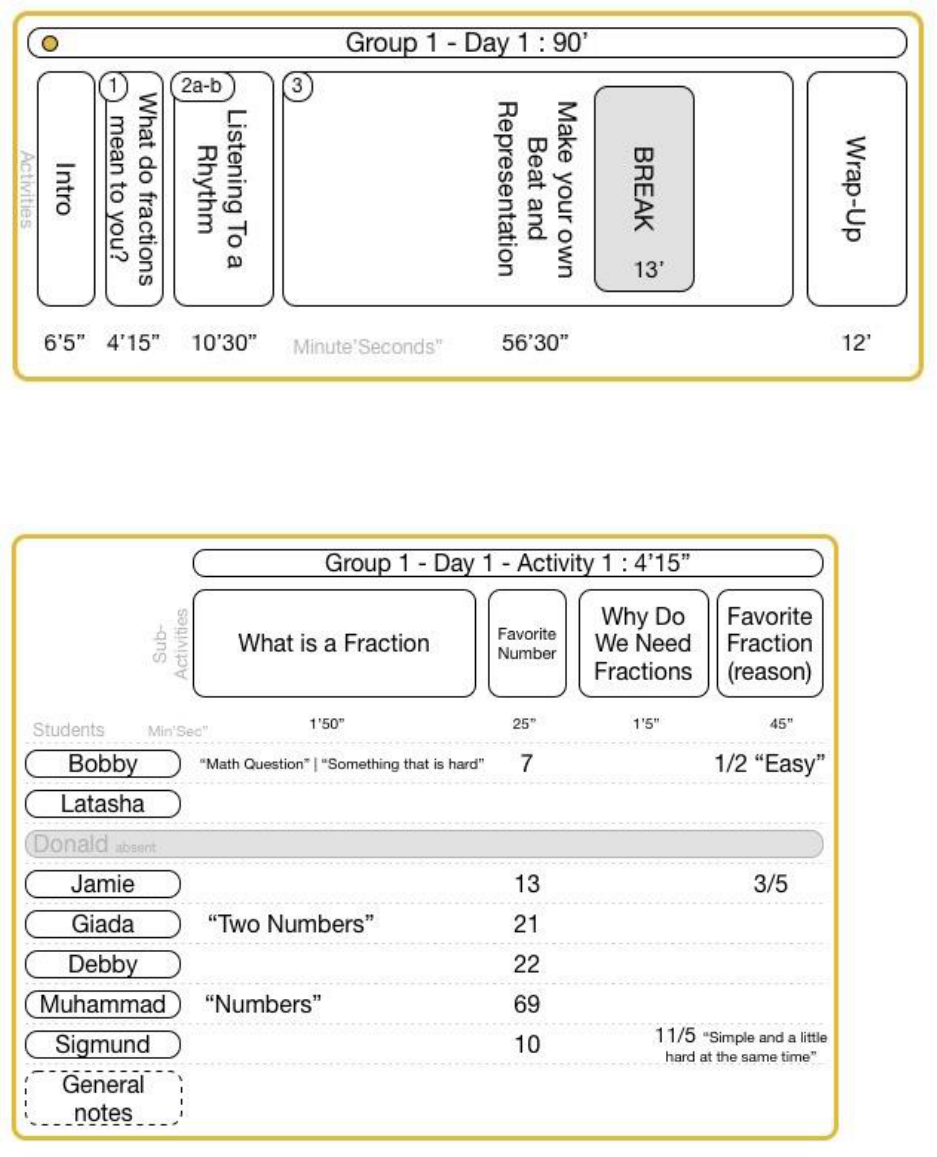
The Sound of Fractions
135
15.5.1 Group 1 Day 1
Figure 15-29 An Overview of Group 1 Day 1 Classroom video data
15.5.1.1 Group 1 Day 1 Activity 1
Figure 15-30 Group 1 Day 1 Activity 1 Classroom video data
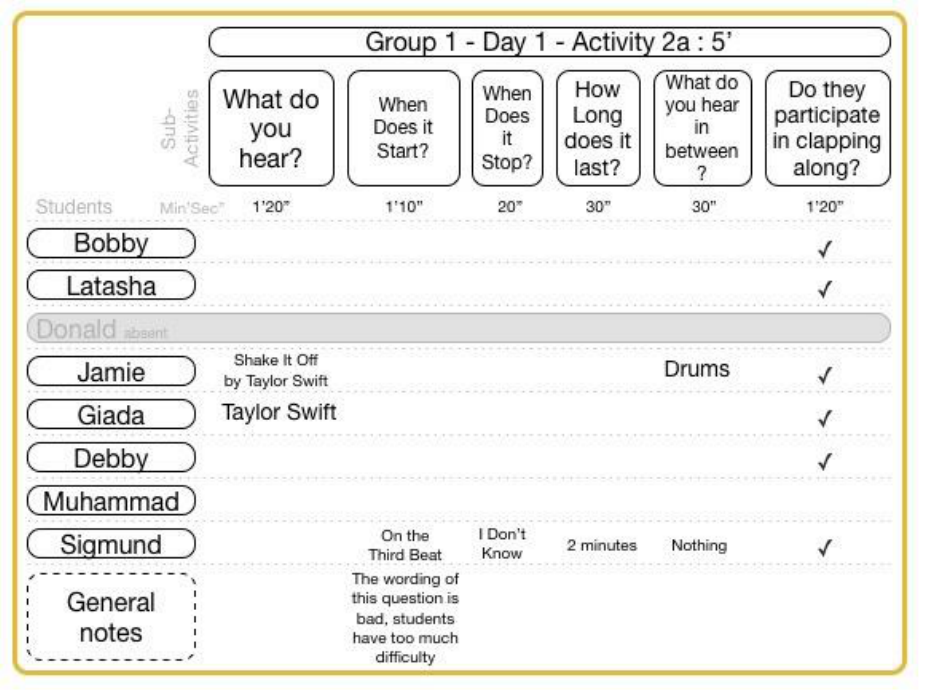
The Sound of Fractions
136
15.5.1.2 Group 1 Day 1 Activity 2 (a and b)
Figure 15-31 Group 1 Day 1 Activity 2a Classroom video data

The Sound of Fractions
137
Figure 15-32 Group 1 Day 1 Activity 2b Classroom video data
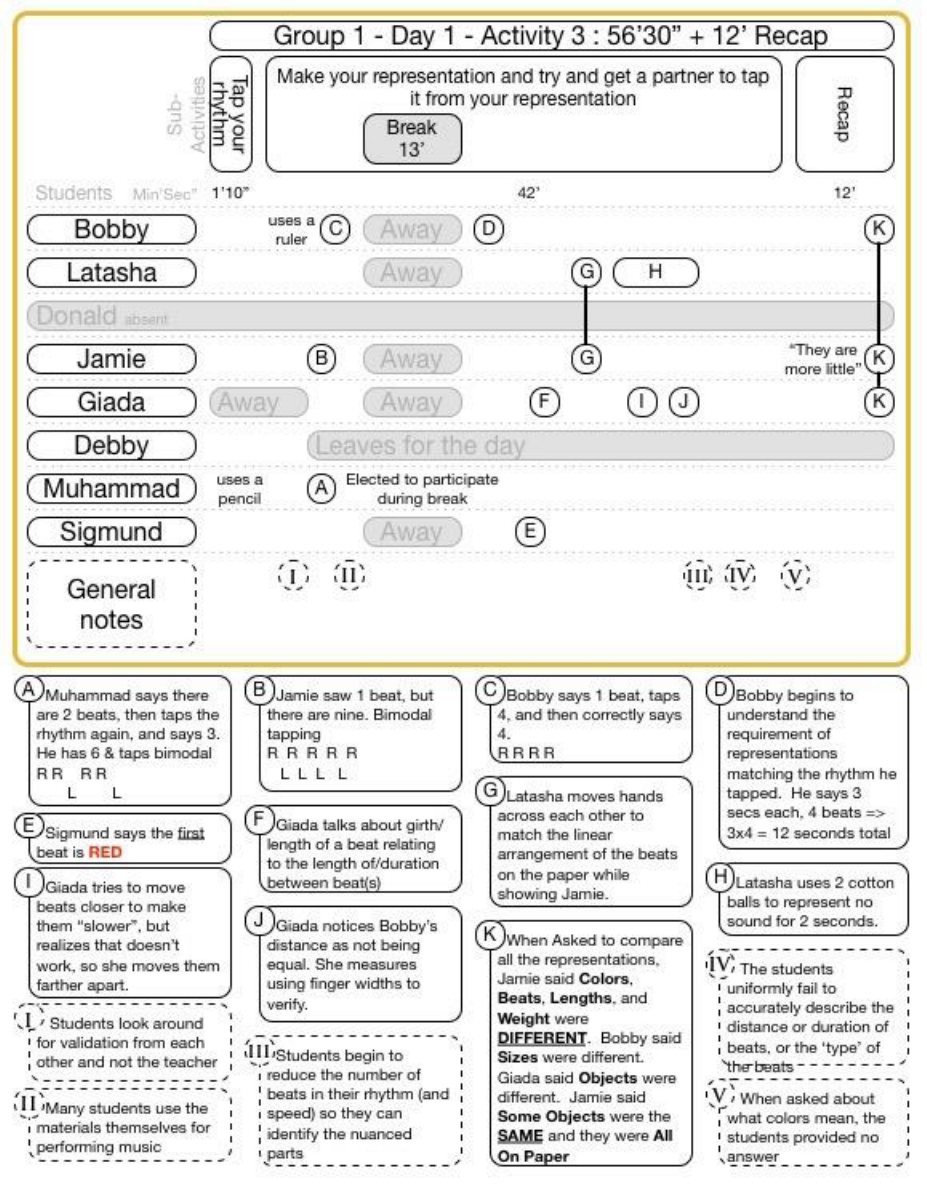
The Sound of Fractions
138
15.5.1.3 Group 1 Day 1 Activity 3
Figure 15-33 Group 1 Day 1 Activity 3 video data

The Sound of Fractions
139
15.5.2 Group 1 Day 2
Figure 15-34 Group 1 Day 2 Overview Classroom video data
15.5.2.1 Group 1 Day 2 Activity 1
Figure 15-35 Group 1 Day 2 Activity 1 Classroom video data

The Sound of Fractions
140
Group 1 Day 2 Activity 2
Figure 15-36 Group 1 Day 2 Activity 2 Classroom video data

The Sound of Fractions
141
15.5.2.2 Group 1 Day 2 Activity 3
Figure 15-37 Group 1 Day 2 Activity 3 Classroom video data
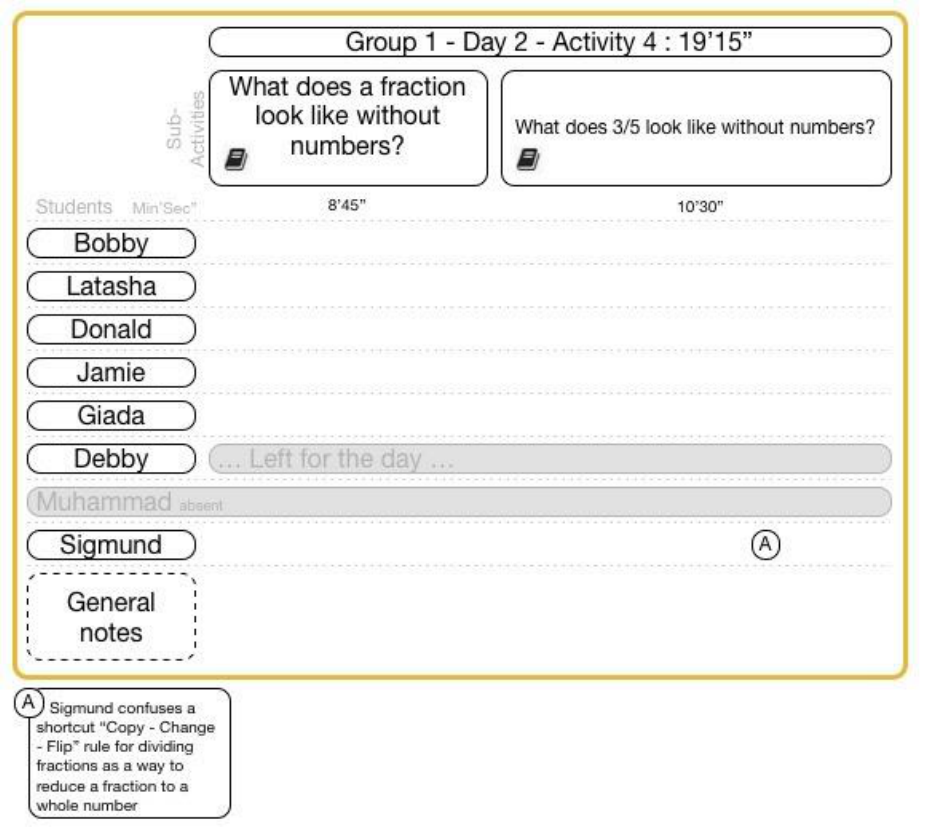
The Sound of Fractions
142
15.5.2.3 Group 1 Day 2 Activity 4
Figure 15-38 Group 1 Day 2 Activity 4 Classroom video data
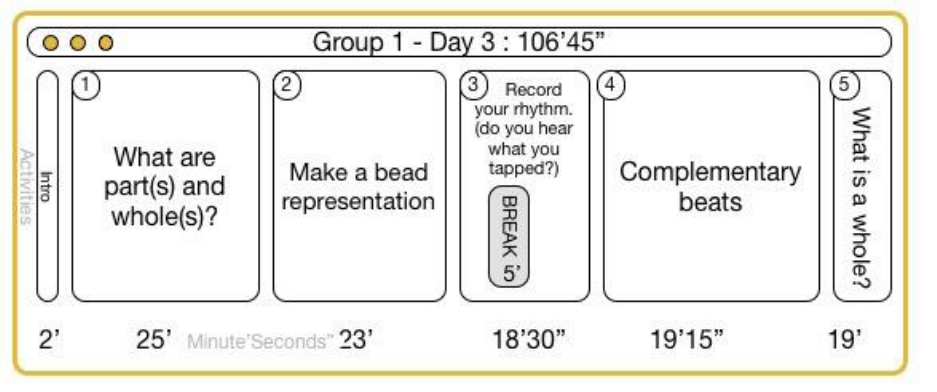
The Sound of Fractions
143
15.5.3 Group 1 Day 3
Figure 15-39 Group 1 Day 3 Overview Classroom video data
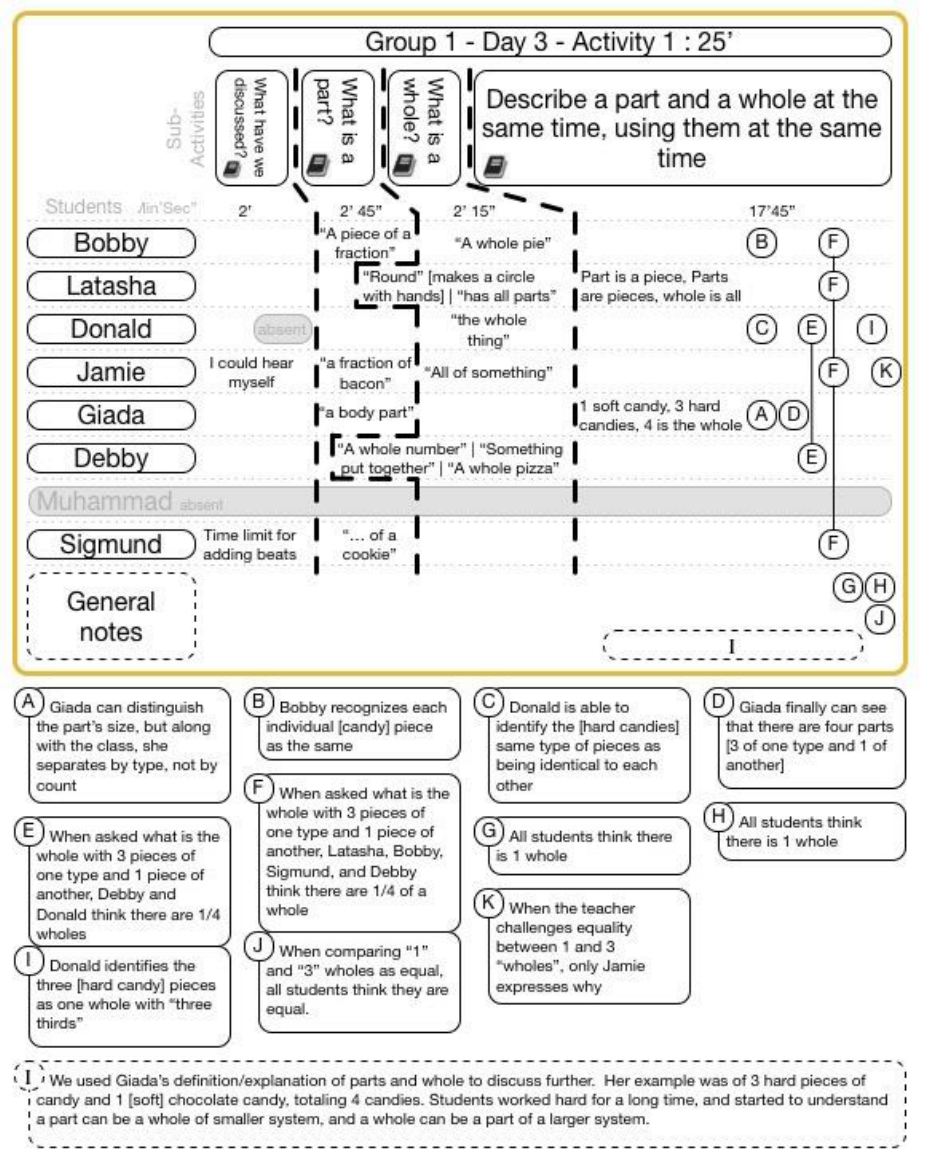
The Sound of Fractions
144
15.5.3.1 Group 1 Day 3 Activity 1
Figure 15-40 Group 1 Day 3 Activity 1 Classroom video data
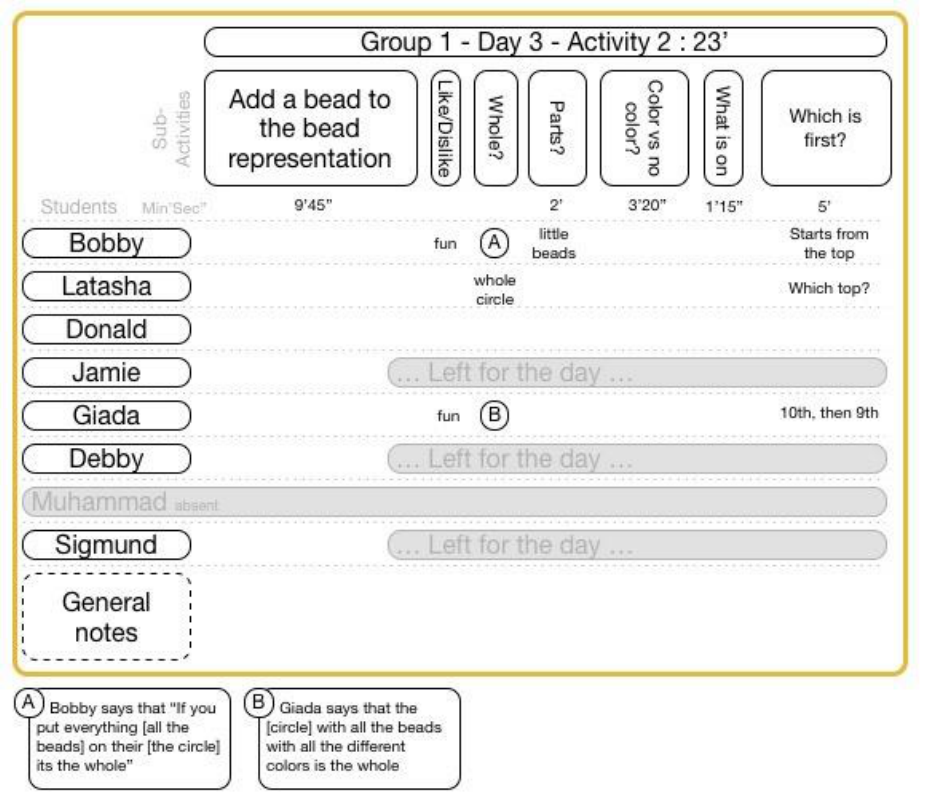
The Sound of Fractions
145
15.5.3.2 Group 1 Day 3 Activity 2
Figure 15-41 Group 1 Day 3 Activity 2 Classroom video data

The Sound of Fractions
146
15.5.3.3 Group 1 Day 3 Activity 3
Figure 15-42 Group 1 Day 3 Activity 3 Classroom video data
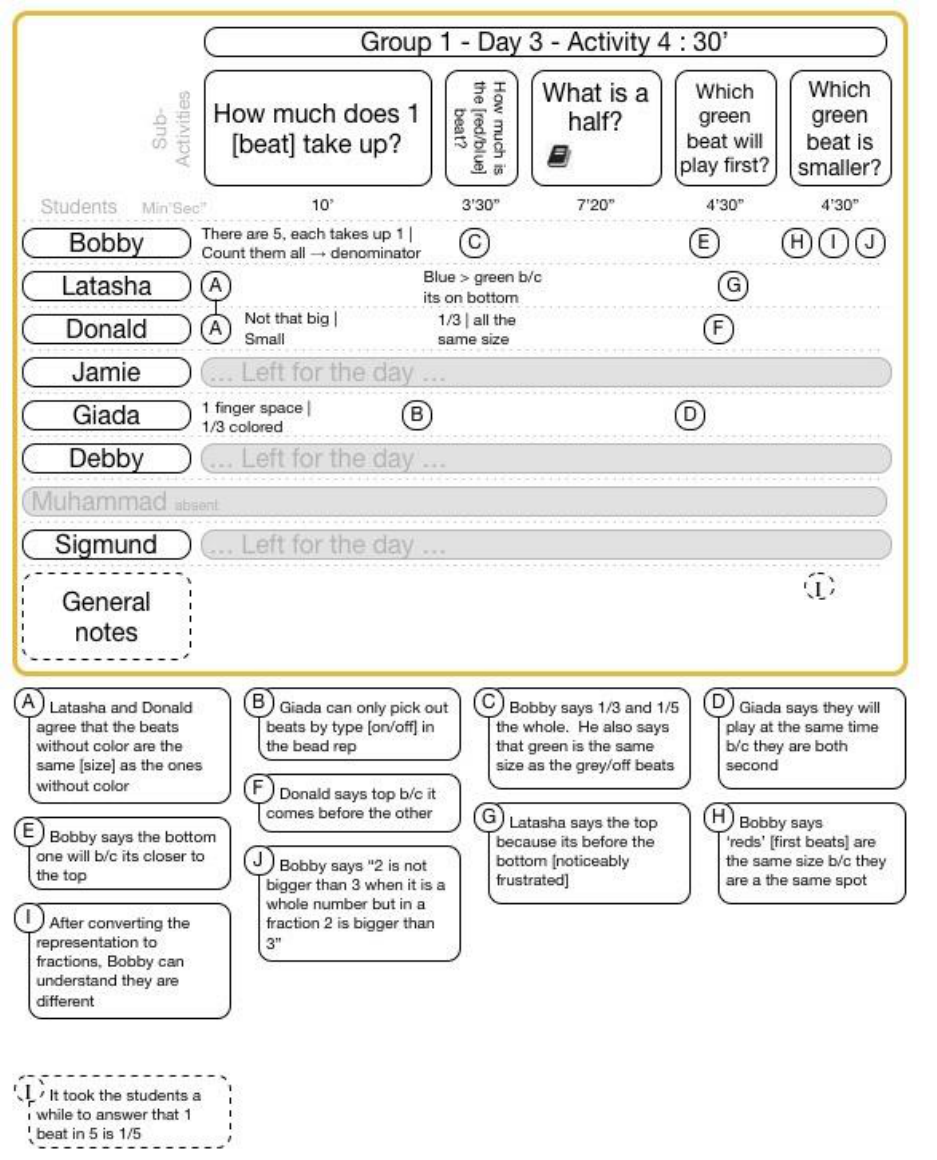
The Sound of Fractions
147
15.5.3.4 Group 1 Day 3 Activity 4
Figure 15-43 Group 1 Day 3 Activity 4 Classroom video data
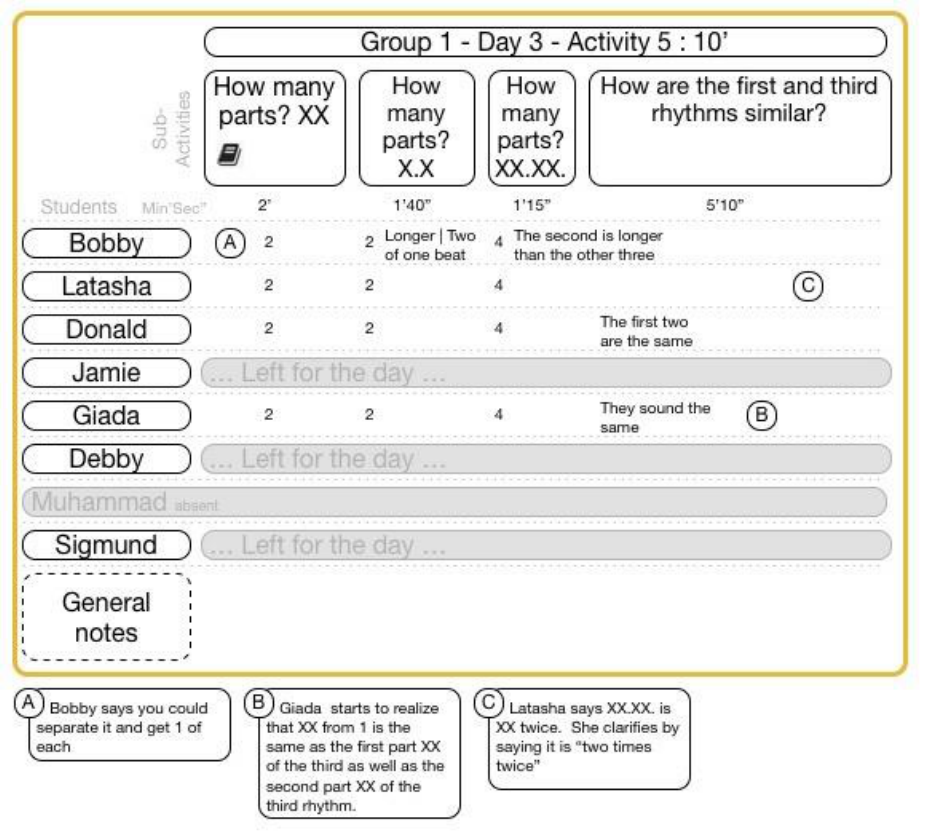
The Sound of Fractions
148
15.5.3.5 Group 1 Day 3 Activity 5
Figure 15-44 Group 1 Day 3 Activity 5 Classroom video data
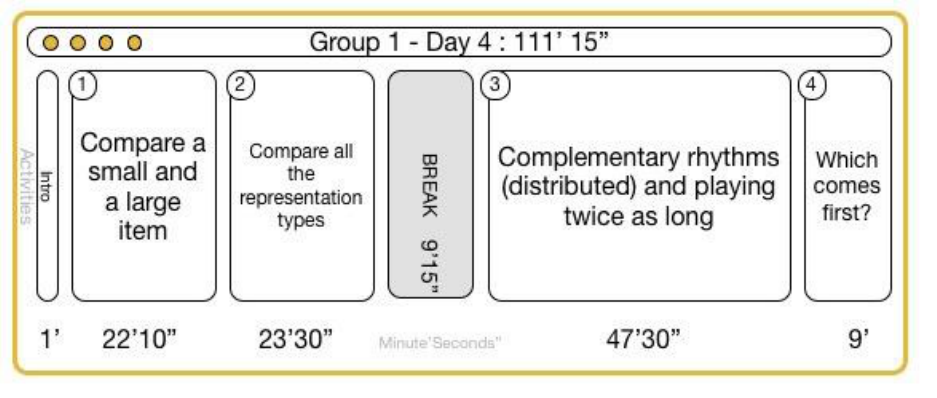
The Sound of Fractions
149
15.5.4 Group 1 Day 4
Figure 15-45 Group 1 Day 4 Overview Classroom video data

The Sound of Fractions
150
15.5.4.1 Group 1 Day 4 Activity 1
Figure 15-46 Group 1 Day 4 Activity 1 Classroom video data

The Sound of Fractions
151
15.5.4.2 Group 1 Day 4 Activity 2
Figure 15-47 Group 1 Day 4 Activity 2 Classroom video data
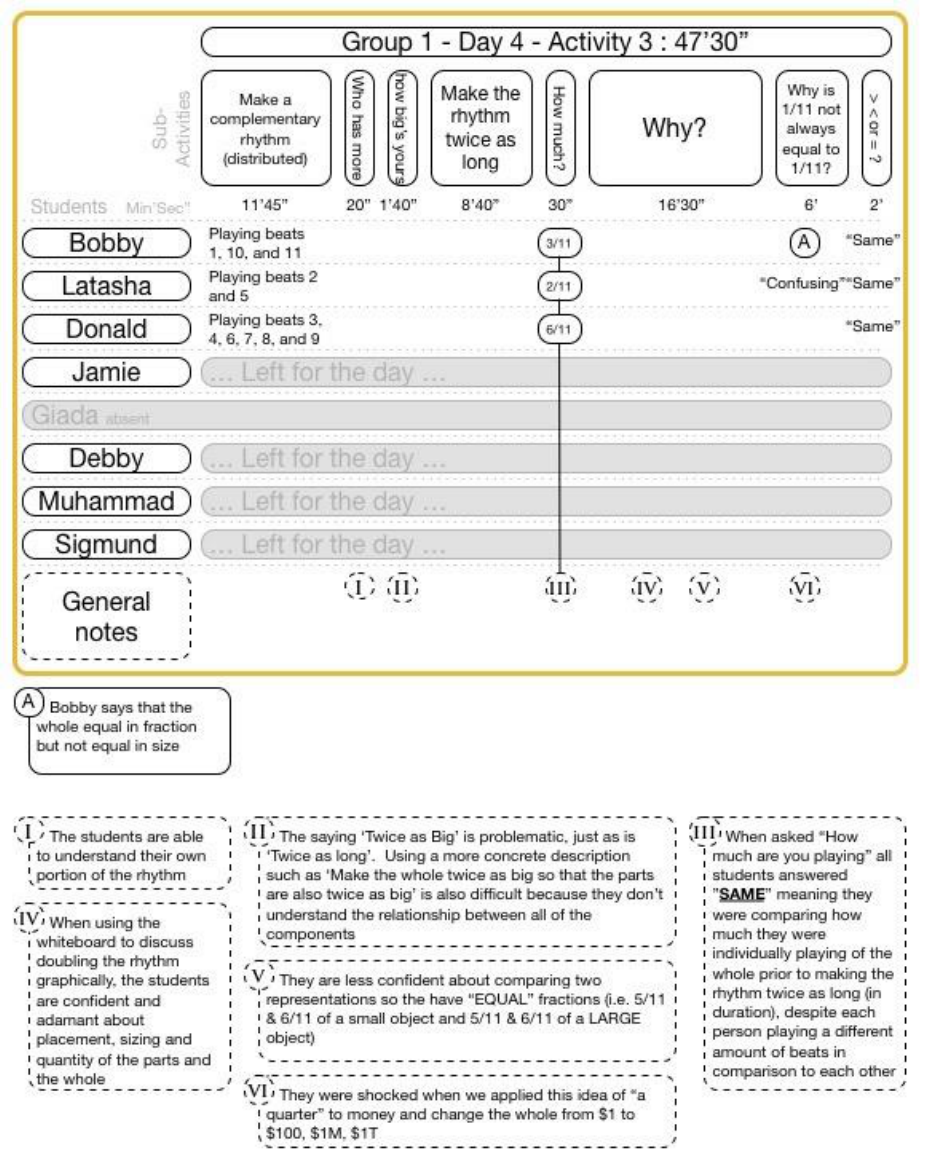
The Sound of Fractions
152
15.5.4.3 Group 1 Day 4 Activity 3

The Sound of Fractions
153
15.5.4.4 Group 1 Day 4 Activity 4
Figure 15-48 Group 1 Day 4 Activity 4
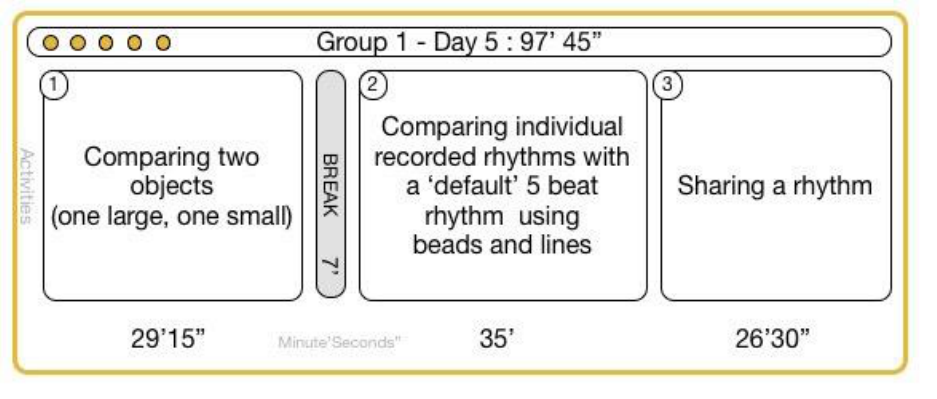
The Sound of Fractions
154
15.5.5 Group 1 Day 5
Figure 15-49 Group 1 Day 5 Overview Classroom video data

The Sound of Fractions
155
15.5.5.1 Group 1 Day 5 Activity 1
Figure 15-50 Group 1 Day 5 Activity 1 Classroom video data
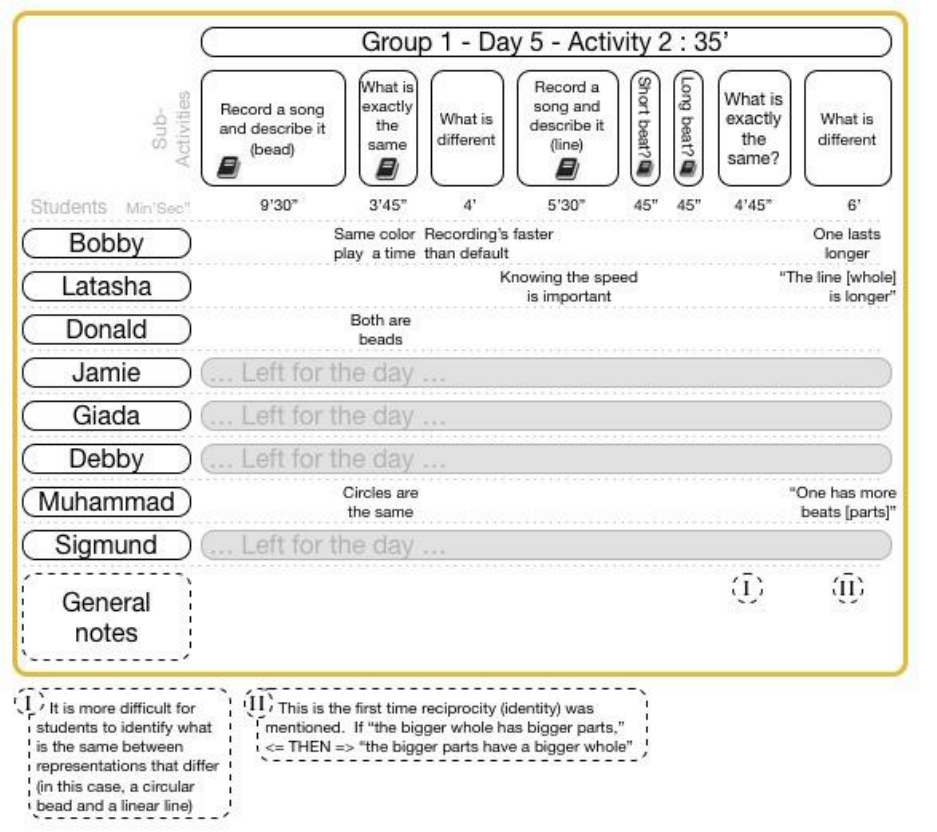
The Sound of Fractions
156
15.5.5.2 Group 1 Day 5 Activity 2
Figure 15-51 Group 1 Day 5 Activity 2 Classroom video data

The Sound of Fractions
157
15.5.5.3 Group 1 Day 5 Activity 3
Figure 15-52 Group 1 Day 5 Activity 3 Classroom video data

The Sound of Fractions
158
15.5.6 Group 1 Day 6
Figure 15-53 Group 1 Day 6 Overview Classroom video data
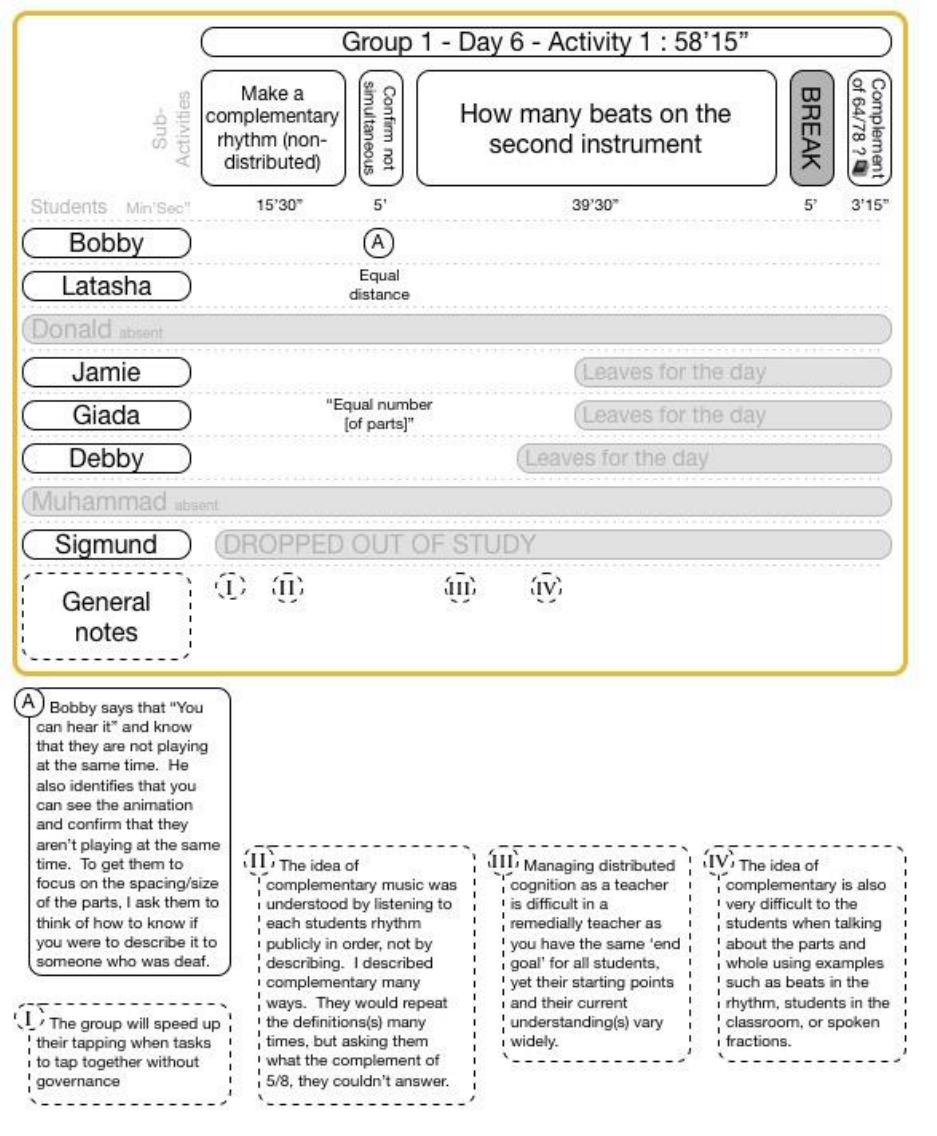
The Sound of Fractions
159
15.5.6.1 Group 1 Day 6 Activity 1
Figure 15-54 Group 1 Day 6 Activity 1 Classroom video data

The Sound of Fractions
160
15.5.6.2 Group 1 Day 6 Activity 2
Figure 15-55 Group 1 Day 6 Activity 2 Classroom video data
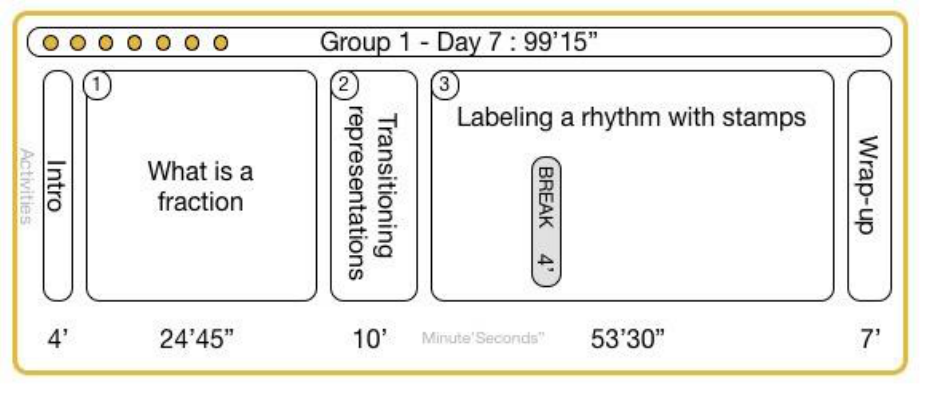
The Sound of Fractions
161
15.5.7 Group 1 Day 7
Figure 15-56 Group 1 Day 7 Overview Classroom video data

The Sound of Fractions
162
15.5.7.1 Group 1 Day 7 Activity 1
Figure 15-57 Group 1 Day 7 Activity 1 Classroom video data
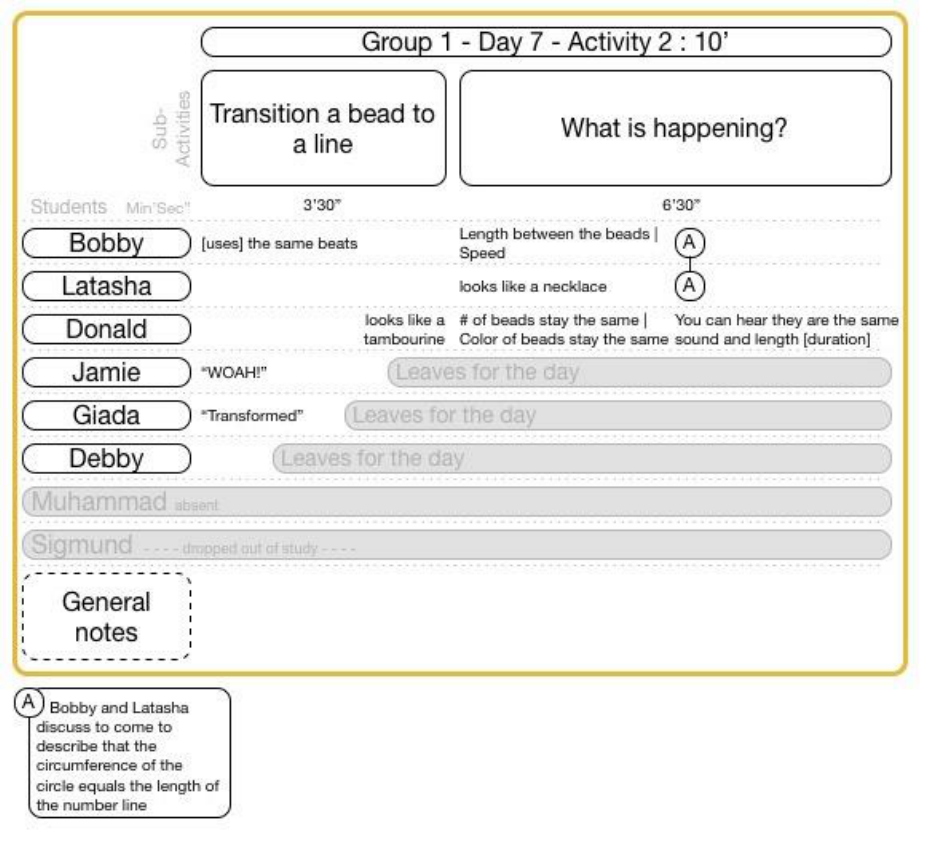
The Sound of Fractions
163
15.5.7.2 Group 1 Day 7 Activity 2
Figure 15-58 Group 1 Day 7 Activity 2 Classroom video data

The Sound of Fractions
164
15.5.7.3 Group 1 Day 7 Activity 3
Figure 15-59 Group 1 Day 7 Activity 3 Classroom video data
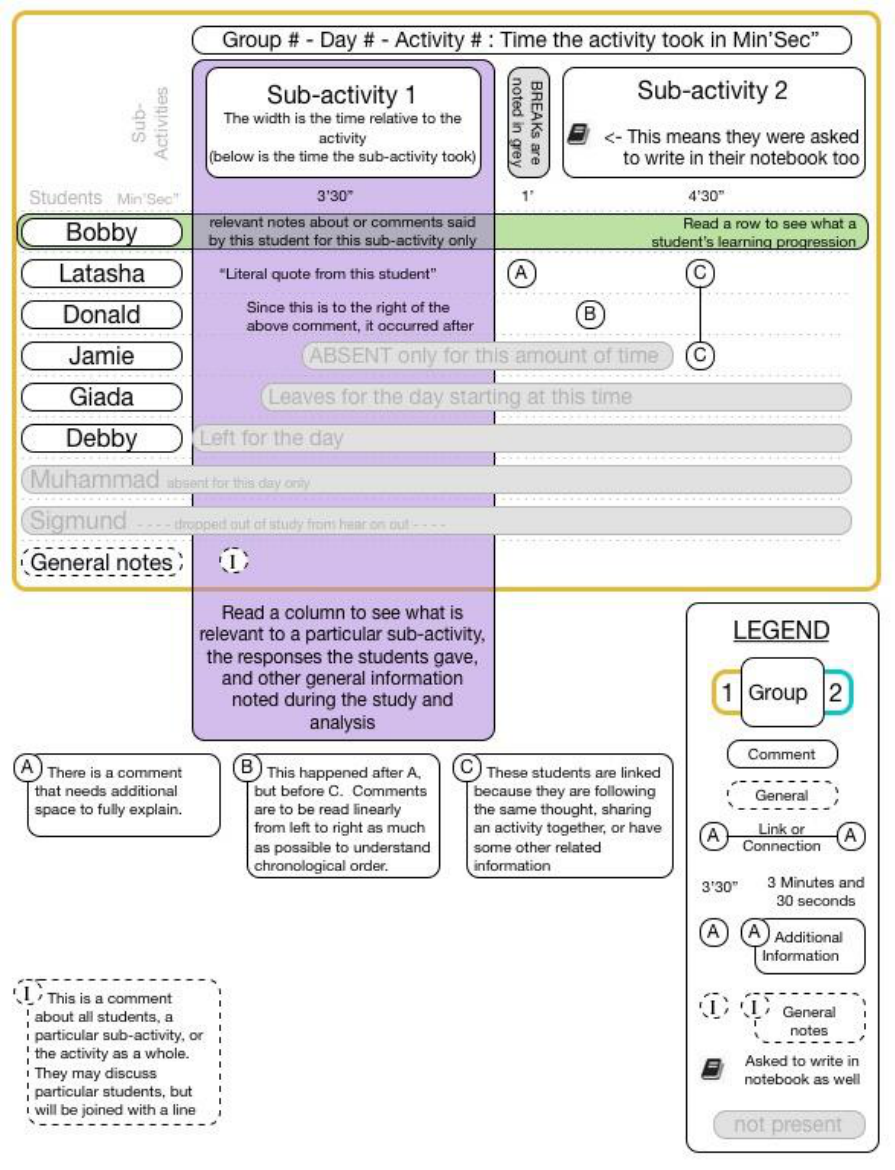
The Sound of Fractions
165
15.6 Group 2 Video Data and Notes
Figure 15-60 A Legend and description for reviewing video data of activities and sub-activities
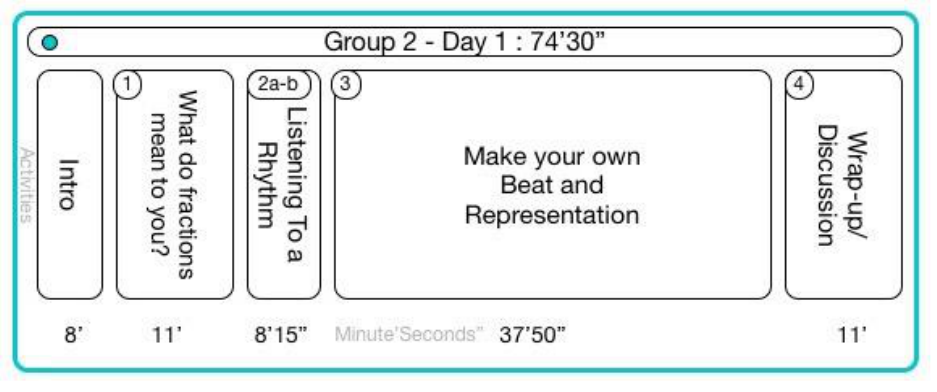
The Sound of Fractions
166
15.6.1 Group 2 Day 1
Figure 15-61 Group 2 Day 1 Overview Classroom video data

The Sound of Fractions
167
15.6.1.1 Group 2 Day 1 Activity 1
Figure 15-62 Group 2 Day 1 Activity 1 Classroom video data
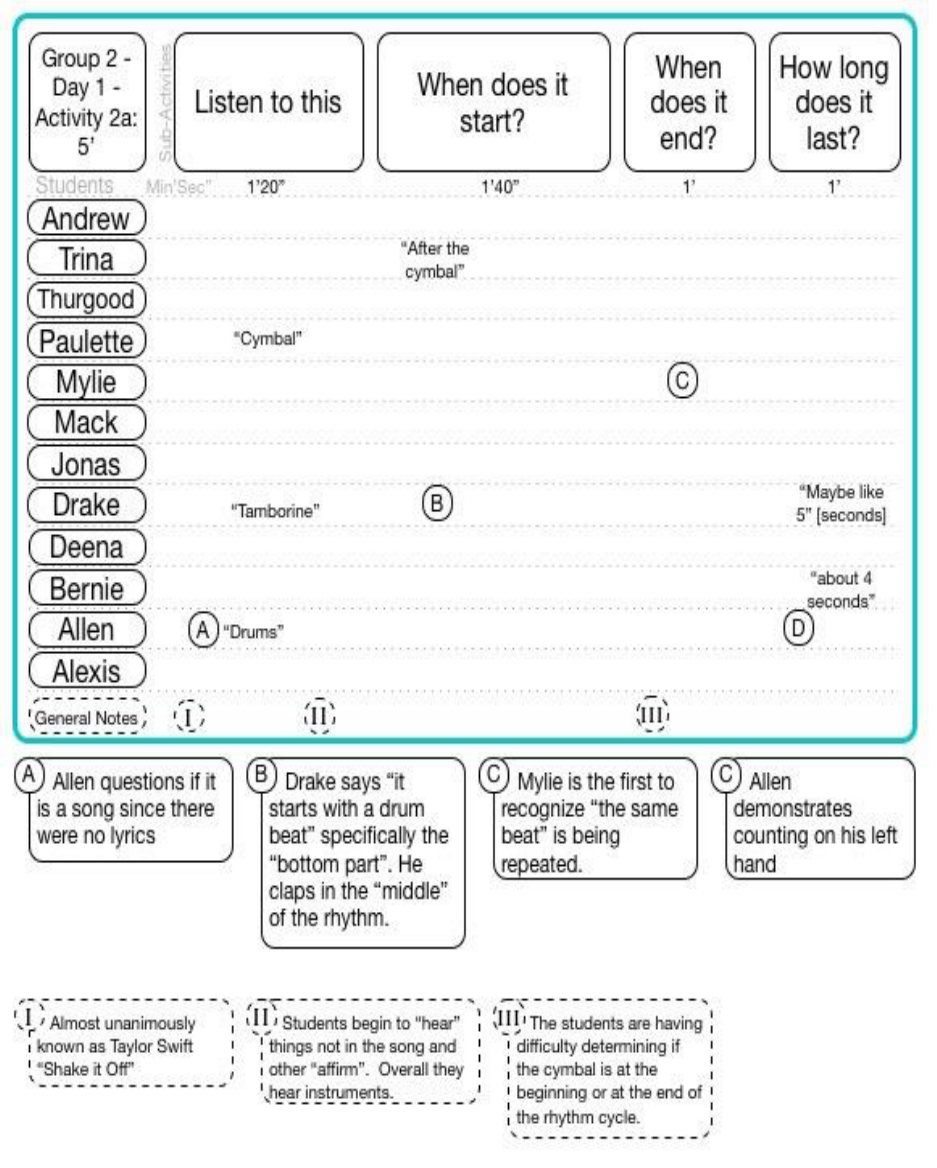
The Sound of Fractions
168
15.6.1.2 Group 2 Day 1 Activity 2 (a and b)
Figure 15-63 Group 2 Day 1 Activity 2a Classroom video data
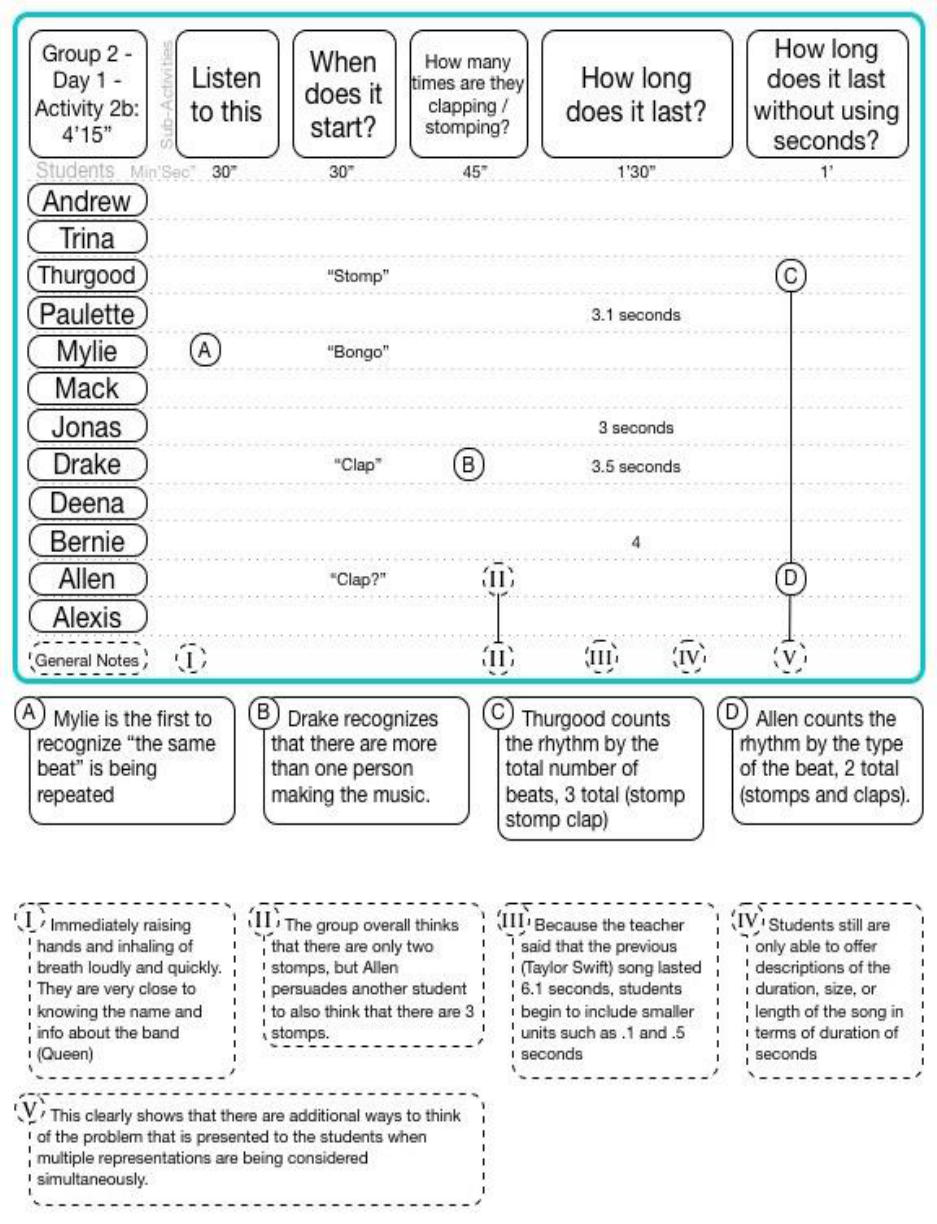
The Sound of Fractions
169
Figure 15-64 Group 2 Day 1 Activity 2b Classroom video data

The Sound of Fractions
170
15.6.1.3 Group 2 Day 1 Activity 3
Figure 15-65 Group 2 Day 1 Activity 3 Classroom video data

The Sound of Fractions
171
15.6.1.4 Group 2 Day 1 Activity 4
Figure 15-66 Group 2 Day 1 Activity 4 Classroom video data
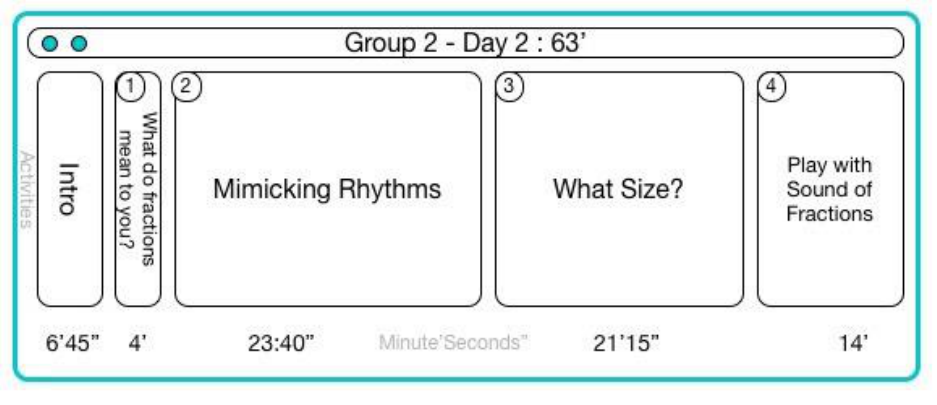
The Sound of Fractions
172
15.6.2 Group 2 Day 2
Figure 15-67 Group 2 Day 2 Overview Classroom video data
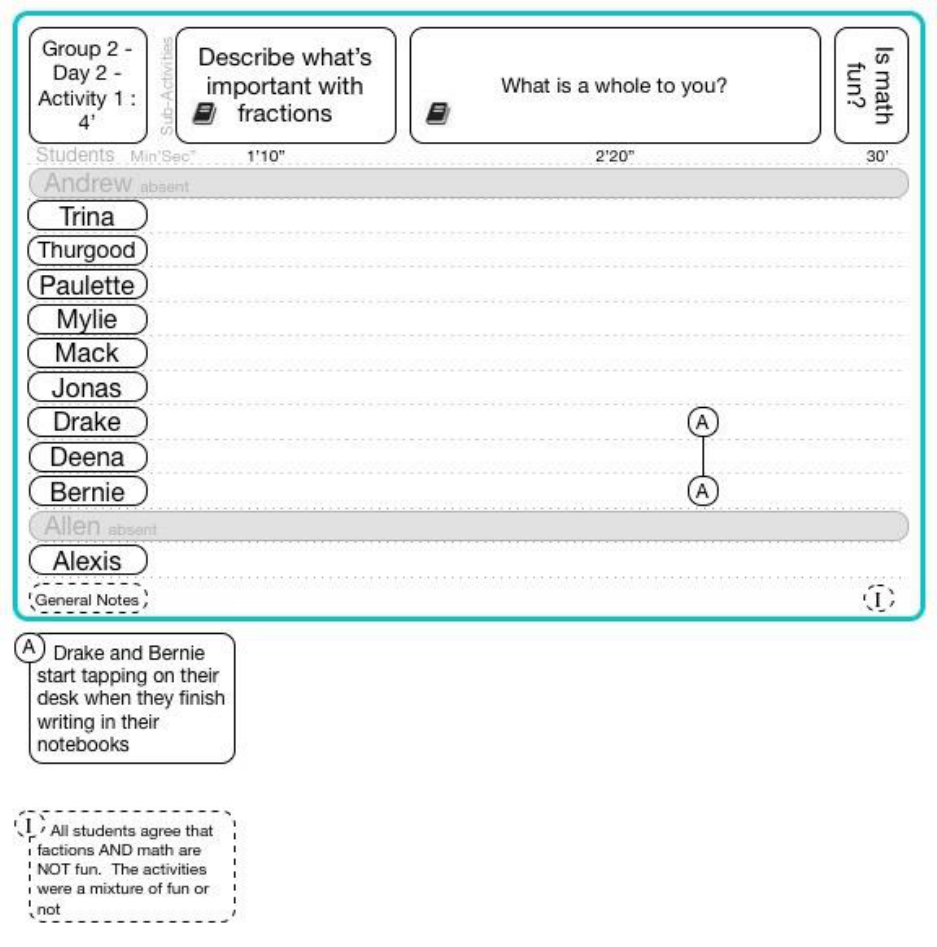
The Sound of Fractions
173
15.6.2.1 Group 2 Day 2 Activity 1
Figure 15-68 Group 2 Day 2 Activity 1 Classroom video data
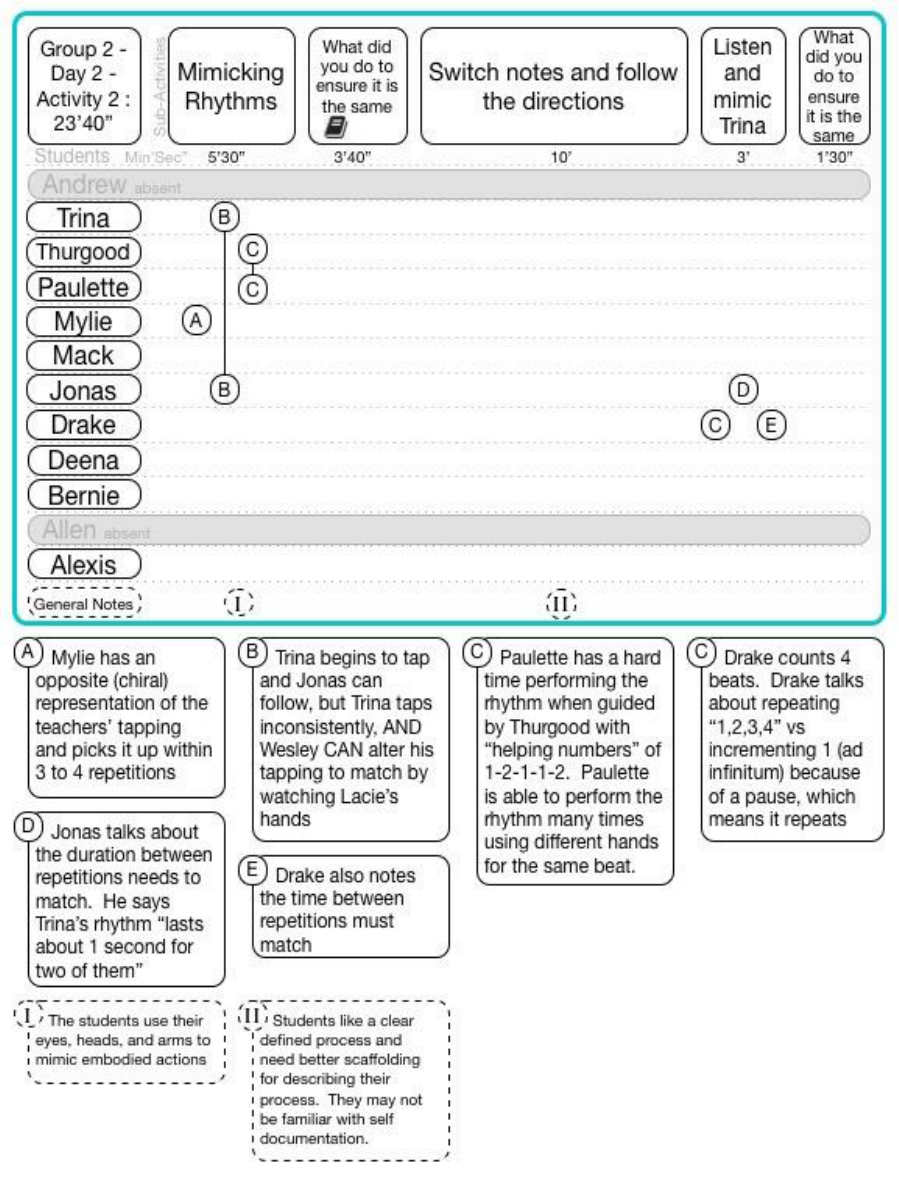
The Sound of Fractions
174
15.6.2.2 Group 2 Day 2 Activity 2
Figure 15-69 Group 2 Day 2 Activity 2 Classroom video data
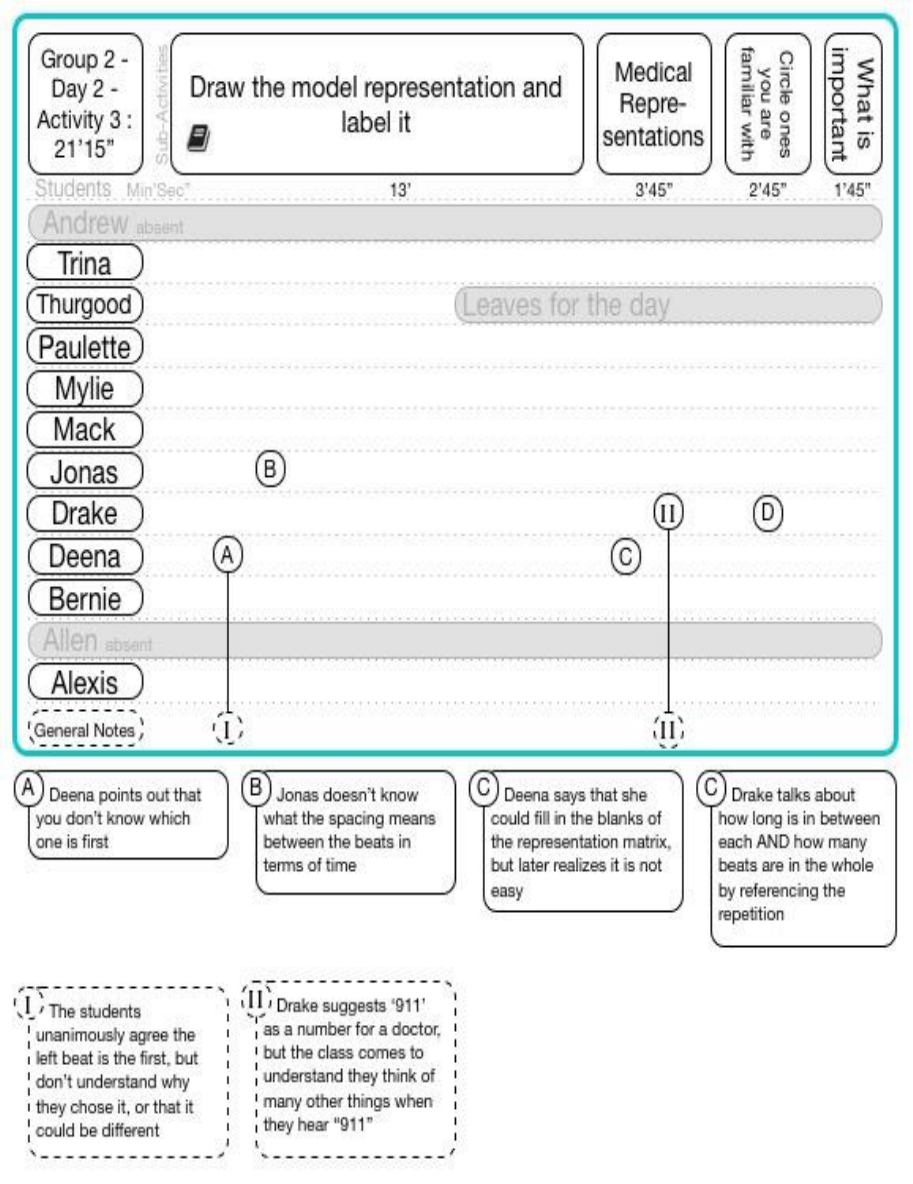
The Sound of Fractions
175
15.6.2.3 Group 2 Day 2 Activity 3
Figure 15-70 Group 2 Day 2 Activity 3 Classroom video data
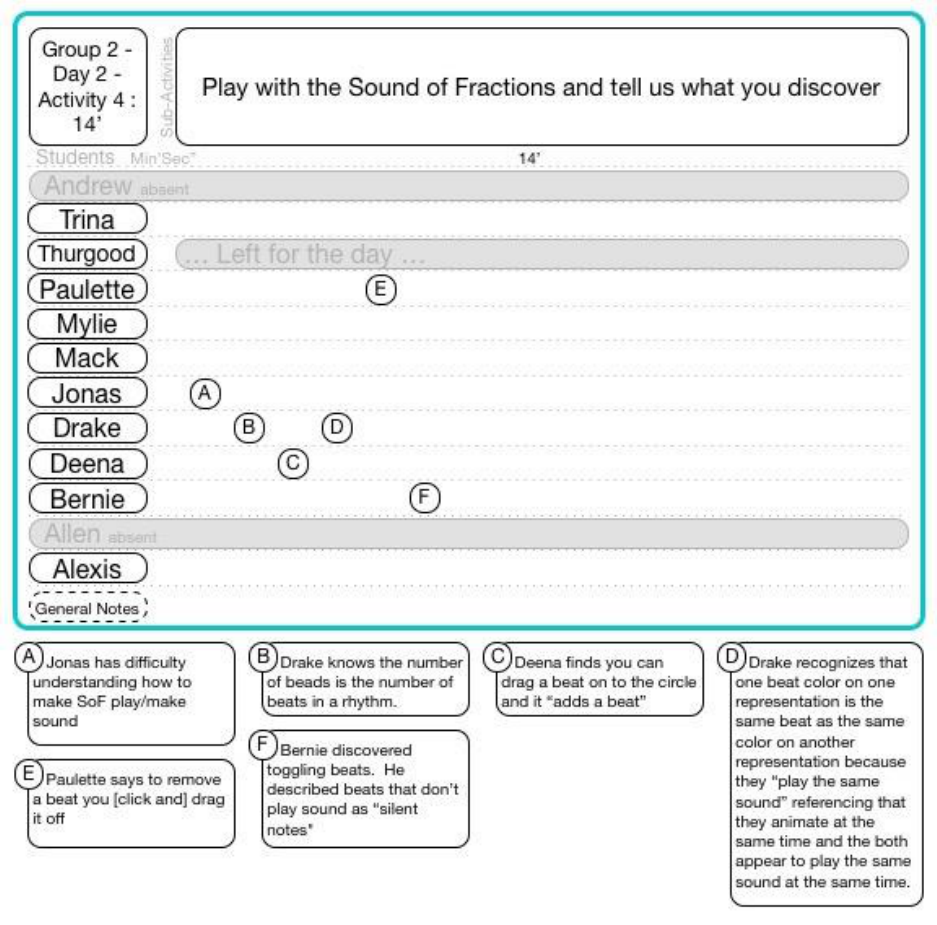
The Sound of Fractions
176
15.6.2.4 Group 2 Day 2 Activity 4
Figure 15-71 Group 2 Day 2 Activity 4 Classroom video data

The Sound of Fractions
177
15.6.3 Group 2 Day 3
Figure 15-72 Group 2 Day 3 Overview Classroom video data

The Sound of Fractions
178
15.6.3.1 Group 2 Day 3 Activity 1
Figure 15-73 Group 2 Day 3 Activity 1 Classroom video data

The Sound of Fractions
179
15.6.3.2 Group 2 Day 3 Activity 2
Figure 15-74 Group 2 Day 3 Activity 2 Classroom video data

The Sound of Fractions
180
15.6.3.3 Group 2 Day 3 Activity 3
Figure 15-75 Group 2 Day 3 Activity 3 video data
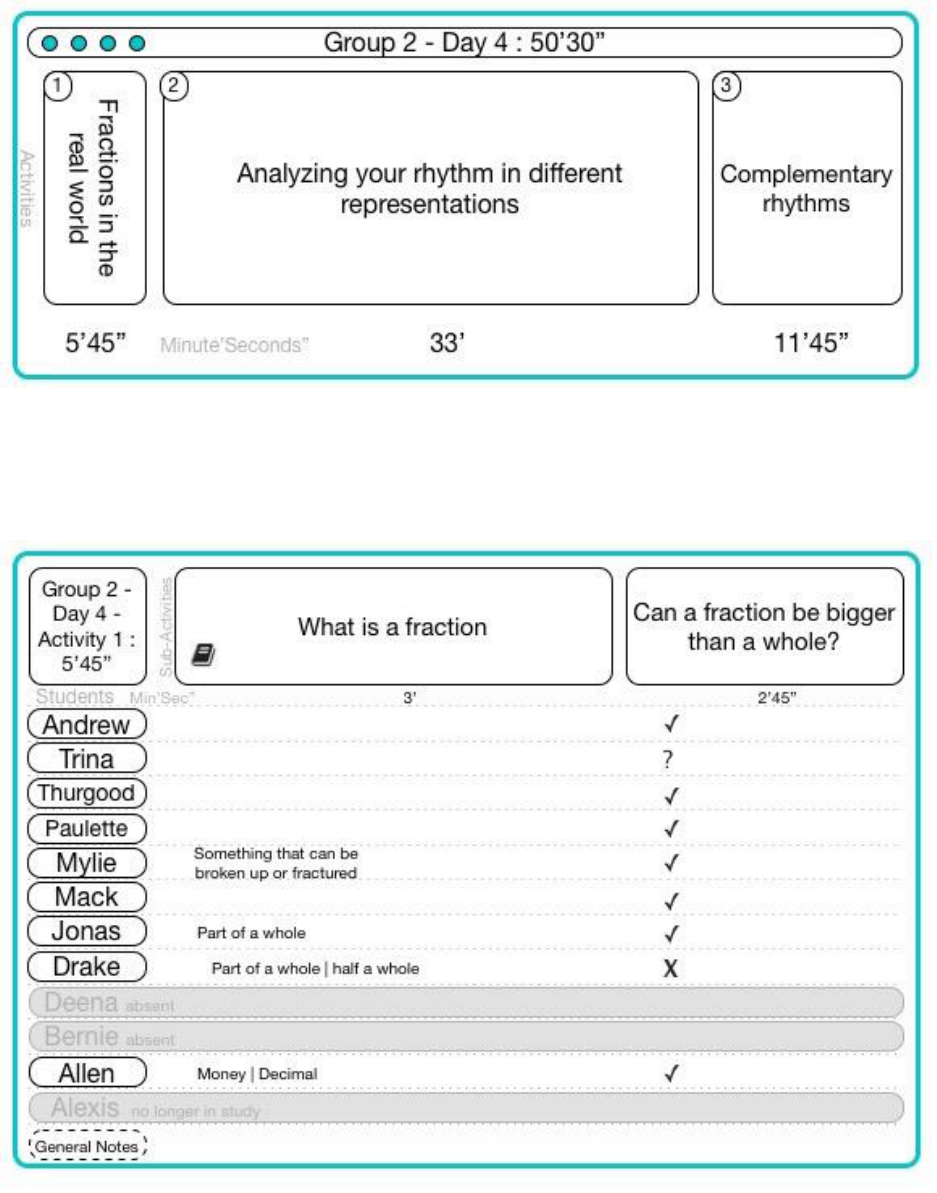
The Sound of Fractions
181
15.6.4 Group 2 Day 4
Figure 15-76 Group 2 Day 4 Overview Classroom video data
15.6.4.1 Group 2 Day 4 Activity 1
Figure 15-77 Group 2 Day 4 Activity 1 Classroom video data
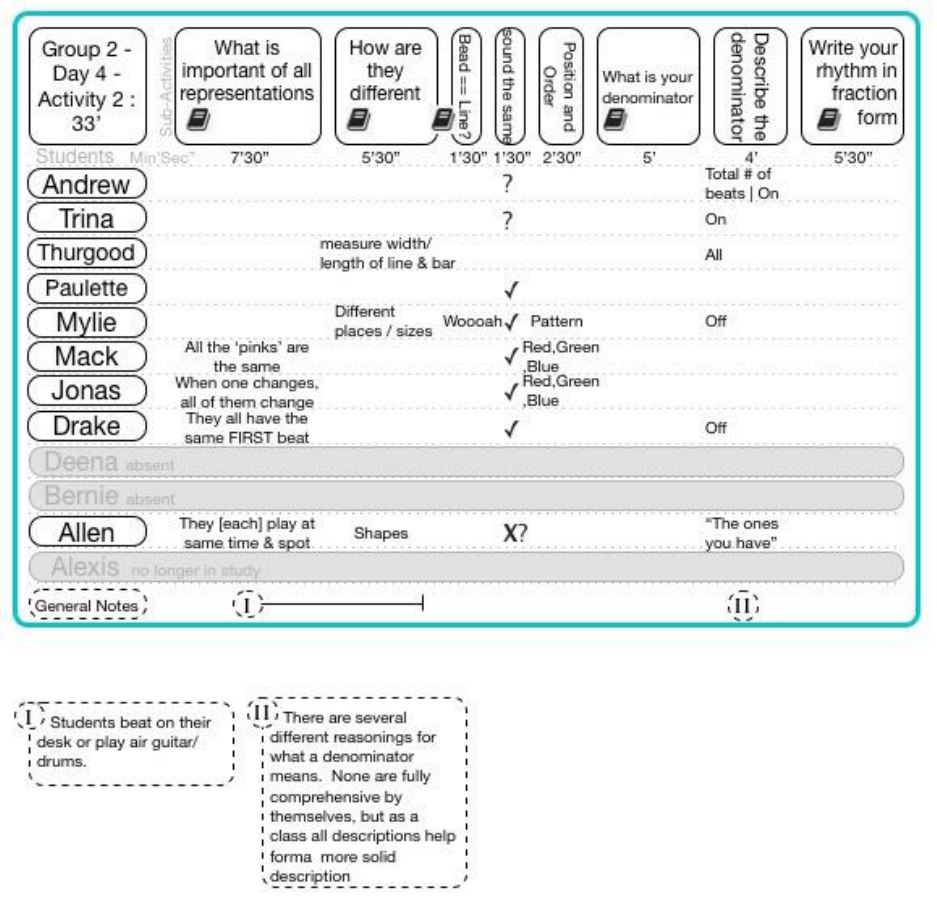
The Sound of Fractions
182
15.6.4.2 Group 2 Day 4 Activity 2
Figure 15-78 Group 2 Day 4 Activity 2 Classroom video data
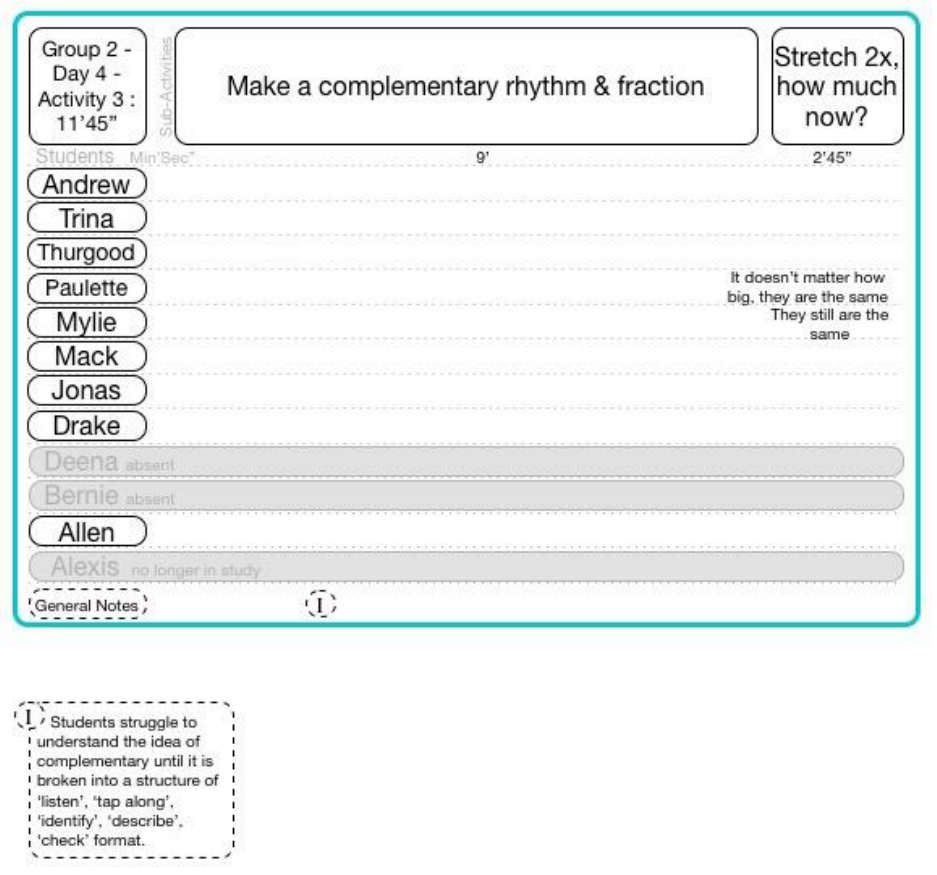
The Sound of Fractions
183
15.6.4.3 Group 2 Day 4 Activity 3
Figure 15-79 Group 2 Day 4 Activity 3 video data
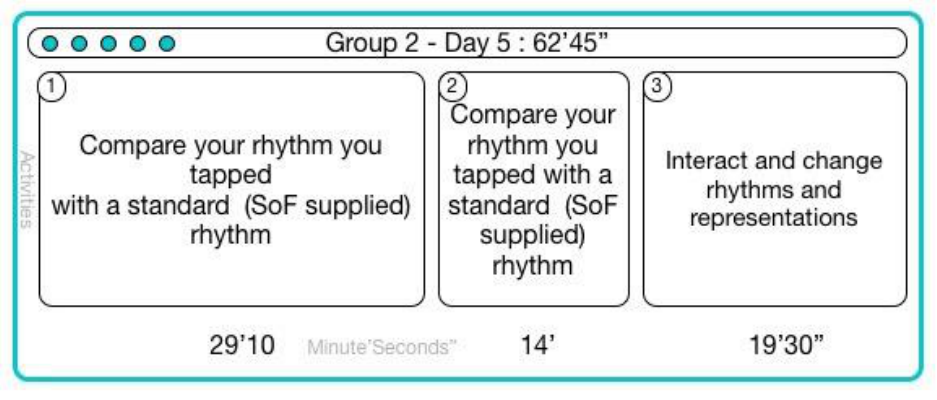
The Sound of Fractions
184
15.6.5 Group 2 Day 5
Figure 15-80 Group 2 Day 5 Overview video data
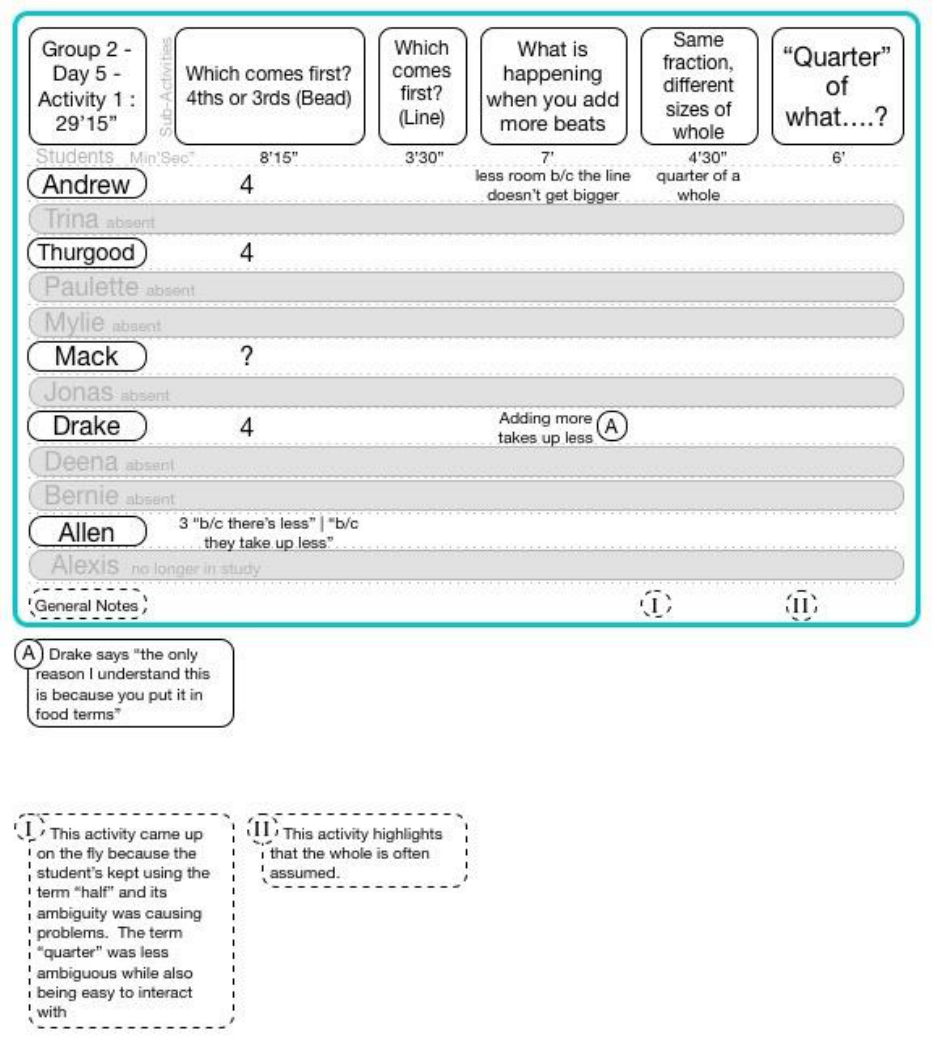
The Sound of Fractions
185
15.6.5.1 Group 2 Day 5 Activity 1
Figure 15-81 Group 2 Day 5 Activity 1 Classroom video data

The Sound of Fractions
186
15.6.5.2 Group 2 Day 5 Activity 2
Figure 15-82 Group 2 Day 5 Activity 2 Classroom video data
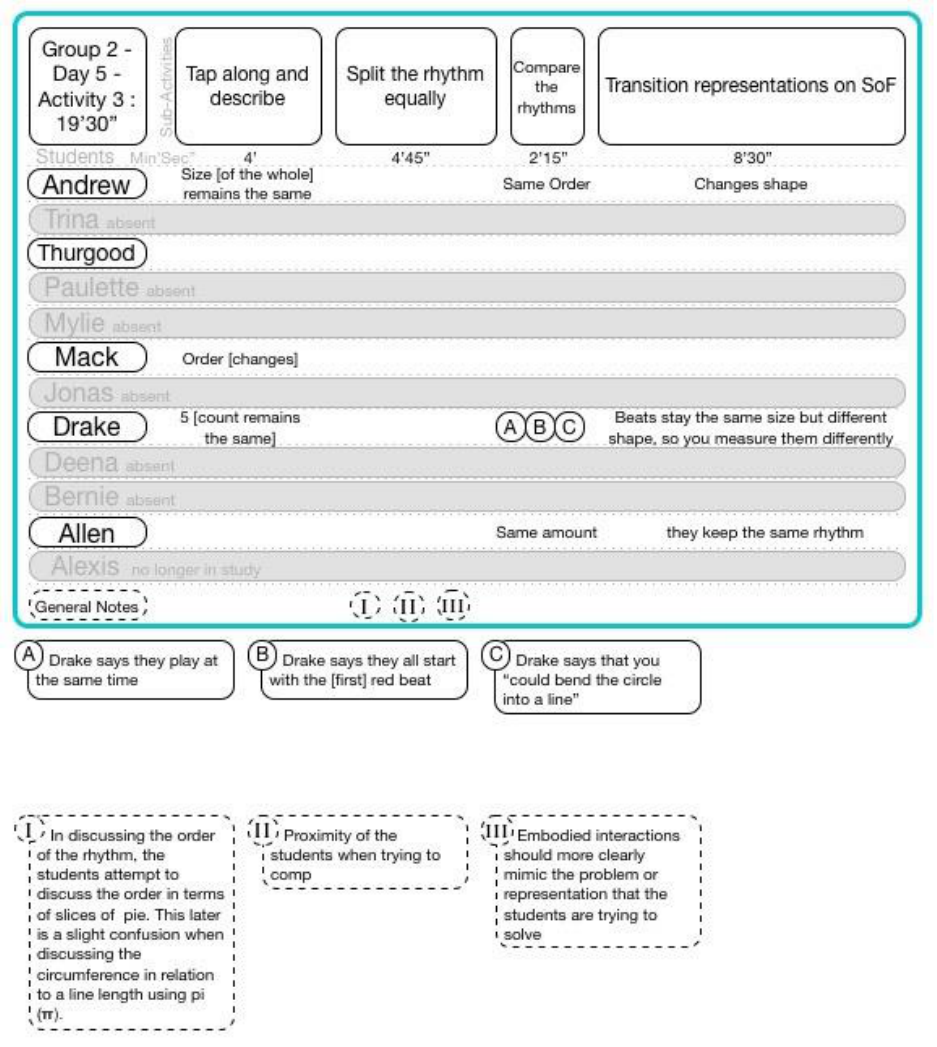
The Sound of Fractions
187
15.6.5.3 Group 2 Day 5 Activity 3
Figure 15-83 Group 2 Day 5 Activity 3 video data

The Sound of Fractions
188
15.6.6 Group 2 Day 6
Figure 15-84 Group 2 Day 6 Overview Classroom video data
15.6.6.1 Group 2 Day 6 Activity 1
Figure 15-85 Group 2 Day 6 Activity 1 Classroom video data
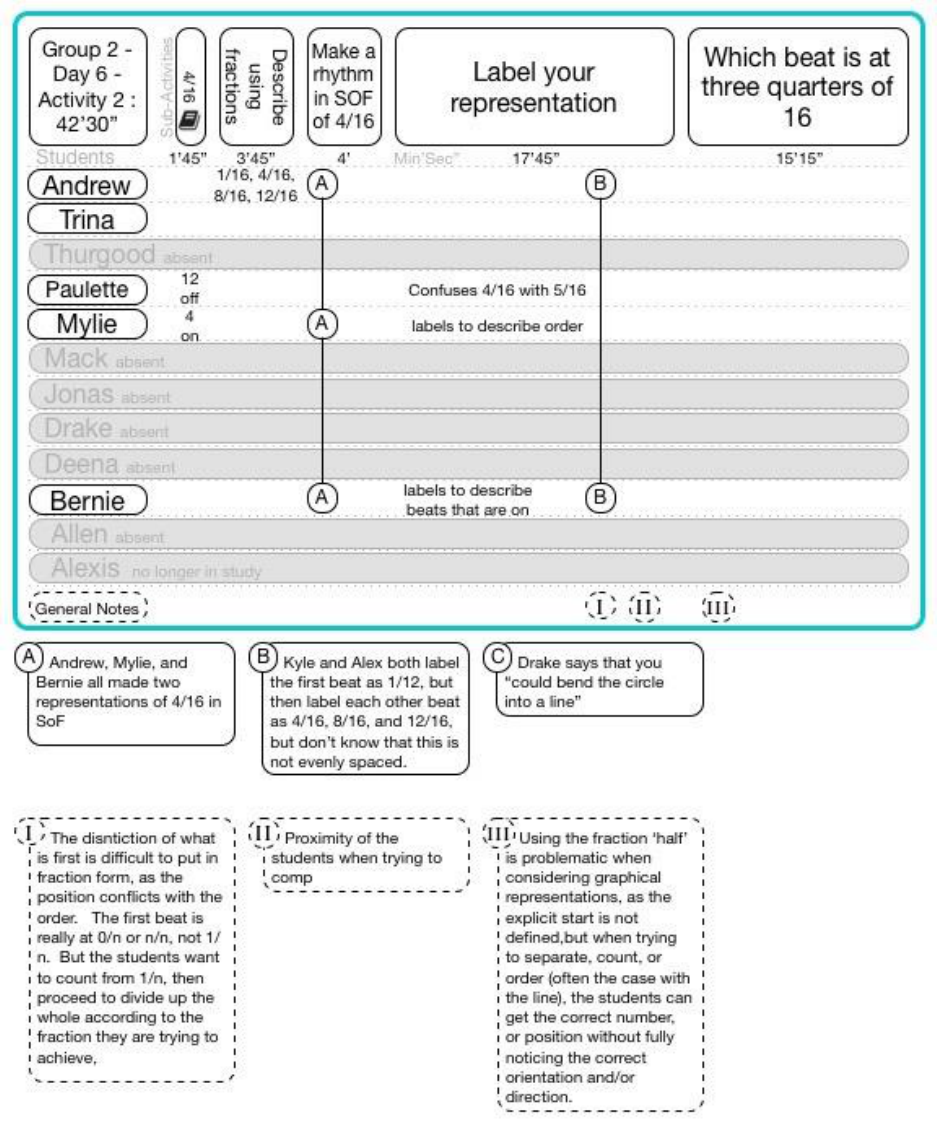
The Sound of Fractions
189
15.6.6.2 Group 2 Day 6 Activity 2
Figure 15-86 Group 2 Day 6 Activity 2 Classroom video data
The Sound of Fractions
190
15.7 Main Code Branch Development Timeline Video
To see the filesystem develop over time, with the many users contribute to its source,
you can watch the following video. One tenth of one second equals one day.
Figure 15-87 A video rendering of a force directed layout of the master branch development of
code for the Sound of Fractions. Also viewable at https://youtu.be/fSM2UkWs2Vs

The Sound of Fractions
191
15.8 Institutional Review Board Certification
The Sound of Fractions
192
Figure 15-88 : IRB Certificate Page
15.9 Indirect References
The Following were referenced during research. Although we are not directly citing
them, we would like to acknowledge that their research came up during our efforts and may
have also helped steer us, albeit unconsciously.
Simmel, G. (1950). The stranger. The Sociology of Georg Simmel, 402–408.
Simon, H. A. (1969). The Sciences of the Artificial (Vol. 136). Cambridge, MA, USA: MIT
Press.
Weeden, R. E. (1972). A comparison of the academic achievement in reading and mathematics
of Negro children whose parents are interested, not interested, or involved in a program of
Suzuki violin. ProQuest Information & Learning.
Fuller, R. B. (1975). Synergetics. Pacific Tape Library.
Shaw, M. (1980). The impact of abstraction concerns on modern programming languages.
Proceedings of the IEEE, 68(9), 1119–1130.
Landers, R. (1984). The Talent Education School of Shinichi Suzuki: An Analysis: Application
of Its Philosophy and Methods to All Areas of Instruction.
d’Ambrosio, U. (1985). Ethnomathematics and its place in the history and pedagogy of
mathematics. For the Learning of Mathematics, 44–48.
Neufeld, K. A. (1986). Understanding of selected pre-number concepts: Relationships to a
formal music program. Alberta Journal of Educational Research.
Alexander, E. R. (1987). Design in planning and decision making: theory and its implications for
practice. In Proceedings of the 1987 conference on planning and design in urban &
regional planning (1987 international congress on planning and design theory, Boston, MA,
17--20 August 1987). ASME, New York (pp. 25–30).
Schön, D. A. (1987). Educating the reflective practitioner: Toward a new design for teaching and
learning in the professions. San Francisco.
D’Ambrosio, U. (1987). Reflections on ethnomathematics. International Study Group on
Ethnomathematics Newsletter, 3(1), 3–5.
Nielsen, J., & Molich, R. (1990). Heuristic evaluation of user interfaces. In Proceedings of the
SIGCHI conference on Human factors in computing systems (pp. 249–256).
The Sound of Fractions
193
Shaw, M. (1990). Prospects for an engineering discipline of software. Software, IEEE, 7(6), 15–
24.
Fish, R. S., Kraut, R. E., Root, R. W., & Rice, R. E. (1992). Evaluating video as a technology for
informal communication. In Proceedings of the SIGCHI conference on Human factors in
computing systems (pp. 37–48).
Carroll, J. M., & Rosson, M. B. (1992). Getting around the task-artifact cycle: how to make
claims and design by scenario. ACM Transactions on Information Systems (TOIS), 10(2),
181–212.
Barten, S. S. (1992). The language of musical instruction. Journal of Aesthetic Education, 53–61.
Buchanan, R. (1992). Wicked problems in design thinking. Design Issues, 5–21.
Feldman, E. B. (1994). Practical art criticism. Prentice Hall New York.
ABELES, H. F., HOFFER, C. F., & KLOTMAN, R. H. (1994). Social Psychological
Foundations Of Music Education. Schimer Book, New York, ABD.
Williams, N. (1995). The Comic Book as Course Book: Why and How.
Kafai, Y. B., & Resnick, M. (1996). Constructionism in practice: Designing, thinking, and
learning in a digital world. Routledge.
Bødker, S. (1996). Creating conditions for participation: Conflicts and resources in systems
development. Human-Computer Interaction, 11(3), 215–236.
Constant, D., Sproull, L., & Kiesler, S. (1996). The kindness of strangers: The usefulness of
electronic weak ties for technical advice. Organization Science, 7(2), 119–135.
Wellman, B. (1997). An electronic group is virtually a social network. Culture of the Internet, 4,
179–205.
Jordan, A., Lindsay, L., & Stanovich, P. J. (1997). Classroom teachers’ instructional interactions
with students who are exceptional, at risk, and typically achieving. Remedial and Special
Education, 18(2), 82–93.
Sinor, J. (1997). The Ideas of Kod{á}ly in America This article on the application of Zolt{á}n
Kod{á}ly’s teaching method in the United States was first published in the Music Educators
Journal in February 1986. Music Educators Journal, 83(5), 37–41.
Story, M. F. (1998). Maximizing usability: the principles of universal design. Assistive
Technology, 10(1), 4–12.
The Sound of Fractions
194
Herbsleb, J. D., & Grinter, R. E. (1999). Architectures, coordination, and distance: Conway’s
law and beyond. IEEE Software, 16(5), 63–70.
Reimer, B. (1999). Facing the Risks of the“ Mozart Effect.” Grand Masters Series. Music
Educators Journal, 86(1), 37–43.
MacKay, W. E. (1999). Is paper safer? The role of paper flight strips in air traffic control. ACM
Transactions on Computer-Human Interaction (TOCHI), 6(4), 311–340.
Hollan, J., Hutchins, E., & Kirsh, D. (2000). Distributed cognition: toward a new foundation for
human-computer interaction research. ACM Transactions on Computer-Human Interaction
(TOCHI), 7(2), 174–196.
Czerwinski, M., Cutrell, E., & Horvitz, E. (2000). Instant messaging and interruption: Influence
of task type on performance. In OZCHI 2000 conference proceedings (Vol. 356, p. 361).
Hetland, L. (2000). Learning to make music enhances spatial reasoning. Journal of Aesthetic
Education, 179–238.
Vaughn, K. (2000). Music and mathematics: Modest support for the oft-claimed relationship.
Journal of Aesthetic Education, 149–166.
Sherin, B. L. (2001). A comparison of programming languages and algebraic notation as
expressive languages for physics. International Journal of Computers for Mathematical
Learning, 6(1), 1–61.
Hartson, H. R., Andre, T. S., & Williges, R. C. (2001). Criteria for evaluating usability
evaluation methods. International Journal of Human-Computer Interaction, 13(4), 373–
410.
Somervell, J., Srinivasan, R., Vasnaik, O., & Woods, K. (2001). Measuring distraction and
awareness caused by graphical and textual displays in the periphery. In Proceedings of the
39th Annual ACM Southeast Conference.
D’Ambrosio, U. (2001). What Is Ethnomathematics, and How Can It Help Children in Schools?.
Teaching Children Mathematics, 7(6), 308–310.
Baker, K., Greenberg, S., & Gutwin, C. (2002). Empirical development of a heuristic evaluation
methodology for shared workspace groupware. In Proceedings of the 2002 ACM conference
on Computer supported cooperative work (pp. 96–105).
Wilson, M. (2002). Six views of embodied cognition. Psychonomic Bulletin & Review, 9(4),
625–636.
The Sound of Fractions
195
Russell, D. M., Drews, C., & Sue, A. (2002). Social aspects of using large public interactive
displays for collaboration. In UbiComp 2002: Ubiquitous Computing (pp. 229–236).
Springer.
Norman, D. A. (2002). The psychpathology of everyday things. Basic books.
Rosson, M. B., & Carroll, J. J. M. (2002). Usability engineering [electronic resource]: scenario-
based development of human-computer interaction. Morgan Kaufmann.
Zhao, Q. A., & Stasko, J. T. (2002). What’s happening?: promoting community awareness
through opportunistic, peripheral interfaces. In Proceedings of the working conference on
advanced visual interfaces (pp. 69–74).
Collective, T. D.-B. R. (2003). Design-based research: An emerging paradigm for educational
inquiry. Educational Researcher, 5–8.
Denning, P. J. (2003). Great principles of computing. Communications of the ACM, 46(11), 15–
20.
Gulliksen, J., Göransson, B., Boivie, I., Blomkvist, S., Persson, J., & Cajander, Å. (2003). Key
principles for user-centred systems design. Behaviour and Information Technology, 22(6),
397–409.
Trafton, J. G., Altmann, E. M., Brock, D. P., & Mintz, F. E. (2003). Preparing to resume an
interrupted task: Effects of prospective goal encoding and retrospective rehearsal.
International Journal of Human-Computer Studies, 58(5), 583–603.
Amrit, C., Hillegersberg, J., & Kumar, K. (2004). A social network perspective of Conway’s
law. In Proceedings of the CSCW Workshop on Social Networks, Chicago, IL, USA.
Collins, A., Joseph, D., & Bielaczyc, K. (2004). Design research: Theoretical and
methodological issues. The Journal of the Learning Sciences, 13(1), 15–42.
Somervell, J. (2004). Developing heuristic evaluation methods for large screen information
exhibits based on critical parameters. Virginia Polytechnic Institute and State University.
Erler, M. F. (2004). Exploring World Cultures with Music. Social Studies and the Young
Learner, 17(1), 30–32.
De Souza, C., Dourish, P., Redmiles, D., Quirk, S., & Trainer, E. (2004). From technical
dependencies to social dependencies. In Workshop on Social Networks for Design and
Analysis: Using Network Information in CSCW.
Bayazit, N. (2004). Investigating design: A review of forty years of design research. Design
Issues, 20(1), 16–29.
The Sound of Fractions
196
Harel, G., & Lim, K. (2004). Mathematics teachers’ knowledge base: Preliminary results. In
Proceeding of the 28th annual meeting of the International Group for the Psychology of
Mathematics Education (Vol. 3, pp. 25–32).
Rogers, Y. (2004). New theoretical approaches for HCI. Annual Review of Information Science
and Technology, 38(1), 87–143.
Viégas, F. B., & Donath, J. (2004). Social network visualization: Can we go beyond the graph. In
Workshop on Social Networks, CSCW (Vol. 4, pp. 6–10).
Tatum, J. S. (2004). The challenge of responsible design. Design Issues, 20(3), 66–80.
Abras, C., Maloney-Krichmar, D., & Preece, J. (2004). User-centered design. Bainbridge, W.
Encyclopedia of Human-Computer Interaction. Thousand Oaks: Sage Publications, 37(4),
445–456.
Dourish, P. (2004). Where the action is: the foundations of embodied interaction. MIT press.
Boehner, K., DePaula, R., Dourish, P., & Sengers, P. (2005). Affect: from information to
interaction. In Proceedings of the 4th decennial conference on Critical computing: between
sense and sensibility (pp. 59–68).
Van Der Aalst, W. M. P., Reijers, H. A., & Song, M. (2005). Discovering social networks from
event logs. Computer Supported Cooperative Work (CSCW), 14(6), 549–593.
Terrenghi, L., Kranz, M., Holleis, P., & Schmidt, A. (2006). A cube to learn: a tangible user
interface for the design of a learning appliance. Personal and Ubiquitous Computing, 10(2-
3), 153–158.
Wing, J. M. (2006). Computational Thinking. COMMUNICATIONS OF THE ACM, Vol. 49(3),
33–35.
Klemmer, S. R., Hartmann, B., & Takayama, L. (2006). How bodies matter: five themes for
interaction design. In Proceedings of the 6th conference on Designing Interactive systems
(pp. 140–149).
Few, S. (2006). Information dashboard design. O’Reilly.
Crick, C., Munz, M., & Scassellati, B. (2006). Synchronization in social tasks: Robotic
drumming. In Robot and Human Interactive Communication, 2006. ROMAN 2006. The
15th IEEE International Symposium on (pp. 97–102).
Gonçalves, M. A., Moreira, B. L., Fox, E. A., & Watson, L. T. (2007). ``What is a good digital
library?’'--A quality model for digital libraries. Information Processing & Management,
43(5), 1416–1437.
The Sound of Fractions
197
Michalowski, M. P., Sabanovic, S., & Kozima, H. (2007). A dancing robot for rhythmic social
interaction. In Human-Robot Interaction (HRI), 2007 2nd ACM/IEEE International
Conference on (pp. 89–96).
Leutenegger, S., & Edgington, J. (2007). A games first approach to teaching introductory
programming. In ACM SIGCSE Bulletin (Vol. 39, pp. 115–118).
Martin, T., Rivale, S. D., & Diller, K. R. (2007). Comparison of student learning in challenge-
based and traditional instruction in biomedical engineering. Ann Biomed Eng, 35(8), 1312–
1323. doi:10.1007/s10439-007-9297-7
Owen, C. (2007). Design thinking: Notes on its nature and use. Design Research Quarterly, 2(1),
16–27.
Cross, N. (2007). From a design science to a design discipline: Understanding designerly ways
of knowing and thinking. Design Research Now, 41–54.
Suchman, L. (2007). Human-machine reconfigurations: Plans and situated actions. Cambridge
University Press.
KRAMER, J. (2007). IS ABSTRACTION THE KEY TO COMPUTING. COMMUNICATIONS
OF THE ACM, 50(5), 27–42.
Petroski, H. (2007). Small things considered: Why there is no perfect design. Random House
LLC.
Gamoran, A. (2007). Standards-based reform and the poverty gap: Lessons for No Child Left
Behind. Brookings Institution Press.
Tatar, D. (2007). The design tensions framework. Human--Computer Interaction, 22(4), 413–
451.
Bonsiepe, G. (2007). The uneasy relationship between design and design research. Design
Research Now, 25–39.
Quarles, J., Lampotang, S., Fischler, I., Fishwick, P., & Lok, B. (2008). Collocated AAR:
augmenting after action review with mixed reality. In Proceedings of the 7th IEEE/ACM
International Symposium on Mixed and Augmented Reality (pp. 107–116).
Wing, J. M. (2008). Computational thinking and thinking about computing. Philos Trans A Math
Phys Eng Sci, 366(1881), 3717–3725. doi:10.1098/rsta.2008.0118
Sicart, M. (2008). Defining game mechanics. Game Studies, 8(2).
The Sound of Fractions
198
Harrison, S., & Tatar, D. (2008). Places: people, events, loci--the relation of semantic frames in
the construction of place. Computer Supported Cooperative Work (CSCW), 17(2-3), 97–
133.
Blackwell, A. (2008). The Abstract is “an Enemy”: Alternative Perspectives to Computational
Thinking. PPIG Lancaster.
Greenberg, S., & Buxton, B. (2008). Usability evaluation considered harmful (some of the time).
In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (pp.
111–120).
Saldana, J. (2009). An introduction to codes and coding. The Coding Manual for Qualitative
Researchers, 1–31.
Pauwels, K., Ambler, T., Clark, B. H., LaPointe, P., Reibstein, D., Skiera, B., … Wiesel, T.
(2009). Dashboards as a service: why, what, how, and what research is needed? Journal of
Service Research.
Zaharias, P., & Poylymenakou, A. (2009). Developing a usability evaluation method for e-
learning applications: Beyond functional usability. Intl. Journal of Human--Computer
Interaction, 25(1), 75–98.
Kirschner, S., & Tomasello, M. (2009). Joint drumming: social context facilitates
synchronization in preschool children. Journal of Experimental Child Psychology, 102(3),
299–314.
Denning, P. J. (2009). The profession of IT Beyond computational thinking. Communications of
the ACM, 52(6), 28–30.
Lu, J. J., & Fletcher, G. H. L. (2009). Thinking about computational thinking. In ACM SIGCSE
Bulletin (Vol. 41, pp. 260–264).
Tan, W., Liu, D., & Bishu, R. (2009). Web evaluation: Heuristic evaluation vs. user testing.
International Journal of Industrial Ergonomics, 39(4), 621–627.
Palen, L., Anderson, K. M., Mark, G., Martin, J., Sicker, D., Palmer, M., & Grunwald, D. (2010).
A vision for technology-mediated support for public participation & assistance in mass
emergencies & disasters. In Proceedings of the 2010 ACM-BCS visions of computer science
conference (p. 8).
Dork, M., Gruen, D., Williamson, C., & Carpendale, S. (2010). A visual backchannel for large-
scale events. Visualization and Computer Graphics, IEEE Transactions on, 16(6), 1129–
1138.
The Sound of Fractions
199
Beaton, B., Harrison, S., & Tatar, D. (2010). Digital drumming: a study of co-located, highly
coordinated, dyadic collaboration. In Proceedings of the SIGCHI Conference on Human
Factors in Computing Systems (pp. 1417–1426).
Hornbæk, K. (2010). Dogmas in the assessment of usability evaluation methods. Behaviour &
Information Technology, 29(1), 97–111.
Schmager, F., Cameron, N., & Noble, J. (2010). GoHotDraw: evaluating the Go programming
language with design patterns. In Evaluation and Usability of Programming Languages and
Tools (p. 10).
Secundo, G., Margherita, A., Elia, G., & Passiante, G. (2010). Intangible assets in higher
education and research: mission, performance or both? Journal of Intellectual Capital,
11(2), 140–157.
Hwang, W., & Salvendy, G. (2010). Number of people required for usability evaluation: the
10\pm2 rule. Communications of the ACM, 53(5), 130–133.
Eckerson, W. W. (2010). Performance dashboards: measuring, monitoring, and managing your
business. John Wiley & Sons.
Council, N. R. (2010). REPORT OF A WORKSHOP ON THE SCOPE AND NATURE OF
Computational Thinking, 114.
Repenning, A., Webb, D., & Ioannidou, A. (2010). Scalable game design and the development of
a checklist for getting computational thinking into public schools. In Proceedings of the
41st ACM technical symposium on Computer science education (pp. 265–269).
Tate, B. A. (2010). Seven languages in seven weeks: a pragmatic guide to learning programming
languages. Pragmatic Bookshelf.
Ruthmann, A., Heines, J. M., Greher, G. R., Laidler, P., & Saulters II, C. (2010). Teaching
computational thinking through musical live coding in scratch. In Proceedings of the 41st
ACM technical symposium on Computer science education (pp. 351–355).
Fisher, D., McDonald, D. W., Brooks, A. L., & Churchill, E. F. (2010). Terms of service, ethics,
and bias: Tapping the social web for cscw research. Computer Supported Cooperative Work
(CSCW), Panel Discussion.
Koh, K. H., Basawapatna, A., Bennett, V., & Repenning, A. (2010). Towards the automatic
recognition of computational thinking for adaptive visual language learning. In Visual
Languages and Human-Centric Computing (VL/HCC), 2010 IEEE Symposium on (pp. 59–
66).
Hirano, S. H., Yeganyan, M. T., Marcu, G., Nguyen, D. H., Boyd, L. A., & Hayes, G. R. (2010).
vSked: evaluation of a system to support classroom activities for children with autism. In
The Sound of Fractions
200
Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (pp.
1633–1642).
Berland, M., & Lee, V. R. (2011). Collaborative strategic board games as a site for distributed
computational thinking. International Journal of Game-Based Learning, 1(2), 65.
Council, N. R. (2011). Computer Science: Reflections of the Field, Reflections from the Field.
National Research Council.
Kafura, D., & Tatar, D. (2011). Initial experience with a computational thinking course for
computer science students. In Proceedings of the 42nd ACM technical symposium on
Computer science education (pp. 251–256).
Vavoula, G., & Sharples, M. (2011). Meeting the challenges in evaluating mobile learning: A 3-
level evaluation framework. Combining E-Learning and M-Learning: New Applications of
Blended Educational Resources, 178.
Council, N. R. (2011). NRC Report of a Workshop of Pedagogical Aspects of Computational
Thinking. National Academy of Sciences.
Knapp, R. B., Kim, J., & André, E. (2011). Physiological signals and their use in augmenting
emotion recognition for human--machine interaction. In Emotion-Oriented Systems (pp.
133–159). Springer.
Basawapatna, A., Koh, K. H., Repenning, A., Webb, D. C., & Marshall, K. S. (2011).
Recognizing computational thinking patterns. In Proceedings of the 42nd ACM technical
symposium on Computer science education (pp. 245–250).
Fisher, D. (2011). Social Media Visualization & Privacy. In Proc. CSCW (pp. 19–23).
Steen, M. (2011). Tensions in human-centred design. CoDesign, 7(1), 45–60.
Choi, I., & Bargar, R. (2012). A playable evolutionary interface for performance and social
engagement. In Intelligent Technologies for Interactive Entertainment (pp. 170–182).
Springer.
Hassenzahl, M., Heidecker, S., Eckoldt, K., Diefenbach, S., & Hillmann, U. (2012). All you need
is love: Current strategies of mediating intimate relationships through technology. ACM
Transactions on Computer-Human Interaction (TOCHI), 19(4), 30.
van Barneveld, A., Arnold, K. E., & Campbell, J. P. (2012). Analytics in higher education:
Establishing a common language. EDUCAUSE Learning Initiative.
Initiative, C. C. S. S., & others. (2012). Common core state standards for English language arts
& literacy in history/social studies, science, and technical subjects. Common Core
Standards Initiative.
The Sound of Fractions
201
Aho, A. V. (2012). Computation and Computational Thinking. The Computer Journal, 55(7), 4.
Sebesta, R. W. (2012). Concepts of Programming Languages.
DiPiro, J. T. (2012). Keeping Your Eyes on the Dashboard. American Journal of Pharmaceutical
Education, 76(3).
Radha, M. (2012). Mediated interactions in musical expression.
Hossain, M. S., Butler, P., Boedihardjo, A. P., & Ramakrishnan, N. (2012). Storytelling in entity
networks to support intelligence analysts. In Proceedings of the 18th ACM SIGKDD
international conference on Knowledge discovery and data mining (pp. 1375–1383).
Kapp, K. M. (2012). The gamification of learning and instruction: game-based methods and
strategies for training and education. Wiley. com.
Rooksby, J., & Sommerville, I. (2012). The management and use of social network sites in a
government department. Computer Supported Cooperative Work (CSCW), 21(4-5), 397–
415.
Murray, T., Wing, L., Woolf, B., Wise, A., Wu, S., Clark, L., … Xu, X. (2013). A Prototype
Facilitators Dashboard: Assessing and visualizing dialogue quality in online deliberations
for education and work. In Submitted to 2013 International Conference on e-Learning, e-
Business, Enterprise Information Systems, and e-Government.
Scott, K. A., & White, M. A. (2013). COMPUGIRLS’Standpoint Culturally Responsive
Computing and Its Effect on Girls of Color. Urban Education, 48(5), 657–681.
Bennett, V. E., Koh, K., & Repenning, A. (2013). Computing creativity: divergence in
computational thinking. In Proceeding of the 44th ACM technical symposium on Computer
science education (pp. 359–364).
Mitchell, J. J., & Ryder, A. J. (2013). Developing and Using Dashboard Indicators in Student
Affairs Assessment. New Directions for Student Services, 2013(142), 71–81.
Kirsh, D. (2013). Embodied cognition and the magical future of interaction design. ACM
Transactions on Computer-Human Interaction (TOCHI), 20(1), 3.
Division, N. C. P. S. A. S. (2013). NORTH CAROLINA END-OF-COURSE TESTS. Retrieved
from http://www.ncpublicschools.org/accountability/testing/eoc/
Suri, J. F. (2013). Rotman on Design: The Best on Design Thinking from Rotman Magazine.
University of Toronto Press.
Norman, D. A. (2013). The Design of Everyday Things: Revised and Expanded Edition. Basic
Books. Retrieved from http://books.google.com/books?id=nVQPAAAAQBAJ
The Sound of Fractions
202
Johnson, L., Adams, S., Cummins, M., Estrada, V., Freeman, A., & Ludgate, H. (2013). The
NMC horizon report: 2013 higher education edition.
Bardzell, J., & Bardzell, S. (2013). What is critical about critical design? In Proceedings of the
SIGCHI conference on human factors in computing systems (pp. 3297–3306).
Wisnioski, M. (2014). ``Suppose the World Were Already Lost’': Worst Case Design and the
Engineering Imagination at Harvey Mudd College. Engineering Studies, (ahead-of-print),
1–22.
Ferri, G., Bardzell, J., Bardzell, S., & Louraine, S. (2014). Analyzing critical designs: categories,
distinctions, and canons of exemplars. In Proceedings of the 2014 conference on Designing
interactive systems (pp. 355–364).
Hui, J. S., Gerber, E. M., & Dow, S. P. (2014). Crowd-based design activities: helping students
connect with users online. In Proceedings of the 2014 conference on Designing interactive
systems (pp. 875–884).
Fox, E. A., & da Silva Torres, R. (2014). Digital Library Technologies: Complex Objects,
Annotation, Ontologies, Classification, Extraction, and Security. Synthesis Lectures on
Information Concepts, Retrieval, and Services, (0), 1–205.
Marlow, J., & Dabbish, L. (2014). From rookie to all-star: professional development in a graphic
design social networking site. In Proceedings of the 17th ACM conference on Computer
supported cooperative work & social computing (pp. 922–933).
Swamy, N., Fournet, C., Rastogi, A., Bhargavan, K., Chen, J., Strub, P.-Y., & Bierman, G.
(2014). Gradual typing embedded securely in JavaScript. In Proceedings of the 41st annual
ACM SIGPLAN-SIGACT symposium on Principles of programming languages (pp. 425–
438).
Knowles, B., Blair, L., Walker, S., Coulton, P., Thomas, L., & Mullagh, L. (2014). Patterns of
persuasion for sustainability. In Proceedings of the 2014 conference on Designing
interactive systems (pp. 1035–1044).
Tatar, D. (2014). Reflecting Our Better Nature. Interactions, 21(3), 46–49. doi:10.1145/2594188
Kavanaugh, A., Tedesco, J. C., & Madondo, K. (2014). Social Media vs. Traditional Internet Use
for Community Involvement: Toward Broadening Participation. In Electronic Participation
(pp. 1–12). Springer.
Wiese, J., Min, J.-K., Hong, J. I., & Zimmerman, J. (2015). ``You Never Call, You Never
Write’': Call and SMS Logs Do Not Always Indicate Tie Strength. In Proceedings of the
2015 conference on Computer supported cooperative work-CSCW’15.
The Sound of Fractions
203
Pierce, J., Sengers, P., Hirsch, T., Jenkins, T., Gaver, W., & DiSalvo, C. (2015). Expanding and
Refining Design and Criticality in HCI. In Proceedings of the 33rd Annual ACM
Conference on Human Factors in Computing Systems (pp. 2083–2092).
K. Luther J. Tolentino, W. W. A. P. B. B. M. A. B. H., & Dow, S. (2015). Structuring,
Aggregating, and Evaluating Crowdsourced Design Critique. In , Vancouver (Ed.), .
Abel, T. (n.d.). Design Education: Incorporating Eye-Tracking Research into the Traditional
Design Studio.
Rich, M. (n.d.). Finding Forrester.
Fox, S., Ulgado, R. R., & Rosner, D. K. (n.d.). Hacking Culture, Not Devices: Access and
Recognition in Feminist Hackerspaces.
15.10 Additional thoughts from the author
After writing this thesis, I am confident of the following:
I still wouldn’t spell rhythm correctly if it weren’t for autocorrect, or a vice that it
resembles an iconic old train facing the right, where the ‘r’ is a caboose, the ‘y’ is the center,
the ‘t’ is where the wood is held to be put into the last ‘h’ smokestack, and the ‘m’ is the guard
that pushes objects out of the way of the train on the tracks. This may seem silly, but the word
‘rhythm’ appears XXXX times in this document. That doesn’t count my years of notes. So while
it is funny that I don’t remember how to spell it with precision immediately, I have a mnemonic
to cover my basis.
These are the words I have learned while in grad school, and thought enough to record
them for later reference - typhlostrophedontically, methystrophedontically, chiasmatically,
henophthalmotyphlostrophedontically, boustrophedontically, orthogonally, penultimate, gruit,
sable, proprioception, exteroceptive, interoceptive, lagniappe, hedonic, shirk, virgule,
patronymic, neologism, semogenesis, lethologica, trichotillomania, miasma, bijection,
heterozygosity, helen, gtts, pick, contumacious, cloying, lunule, petrichor, aglet, phloem, drupe,
preantepenultimate, pulchritudinous, callipygian, antepenultimate, propreantepenultimate,
somaesthetics, sentential, lexicographical, vartiwell, subsume, pentheraphobia, blaxploitation,
purposive, praxiology, bisceps, bicepses, flummox, fledging, vacillate, dour, vamp, abecedarian,
arity, blat, asymptotic, contrapositive, aleph, sybaritic, quixotic, bigram, hapax, hapax, velleity,
veridical, obverse, hilt, pervade, absquatulate, caroom, ramify, propinquity, homophily, boon,
micturate, explanandum, start, undergird, doatingly, ambisinister, lemma, ablation,
nosocomial, polsemy, olfactory, and finally din.
XXX Things to compile for final printing XXXX
- Count how many times `rhythm exists in this document’

16 BIBLIOGRAPHY
ABELES, H. F., HOFFER, C. F., & KLOTMAN, R. H. (1994). Social Psychological Foundations Of
Music Education. Schimer Book, New York, ABD.
Acotto, E., & Andreatta, M. (2012). Between mind and mathematics. Different kinds of
computational representations of music. Math{é}matiques et Sciences Humaines.
Mathematics and Social Sciences, (199), 7–25.
Barten, S. S. (1992). The language of musical instruction. Journal of Aesthetic Education, 53–61.
Beaton, B., Harrison, S., & Tatar, D. (2010). Digital drumming: a study of co-located, highly
coordinated, dyadic collaboration. In Proceedings of the SIGCHI Conference on Human
Factors in Computing Systems (pp. 1417–1426).
Behr, M., Harel, G., Post, T., Lesh, R., & Grouws, D. A. (1992). Handbook of research on
mathematics teaching and learning. Rational Number, Ratio. and Proportion. In D. Grouws
(Ed.), Macmillan, New York.
Blaine, T., & Perkis, T. (2000). The Jam-O-Drum interactive music system: a study in interaction
design. In Proceedings of the 3rd conference on Designing interactive systems: processes,
practices, methods, and techniques (pp. 165–173).
Cole, M. (1998). Cultural psychology: A once and future discipline. Harvard University Press.
Confrey, J. (1994). Multiplication and Exponential Functions. The Development of Multiplicative
Reasoning in the Learning of Mathematics, 291.
Courey, S. J., Balogh, E., Siker, J. R., & Paik, J. (2012). Academic music: music instruction to
engage third-grade students in learning basic fraction concepts. Educational Studies in
Mathematics, 81(2), 251–278. doi:10.1007/s10649-012-9395-9
Cummins, F. (2009). Rhythm as an affordance for the entrainment of movement. Phonetica,
66(1-2), 15–28.
D’Ambrosio, U. (1987). Reflections on ethnomathematics. International Study Group on
Ethnomathematics Newsletter, 3(1), 3–5.
D’Ambrosio, U. (2001). What Is Ethnomathematics, and How Can It Help Children in Schools?.
Teaching Children Mathematics, 7(6), 308–310.
Davis, G. E., & Pitkethly, A. (1990). Cognitive aspects of sharing. Journal for Research in
Mathematics Education, 145–153.
Dourish, P. (2004). Where the action is: the foundations of embodied interaction. MIT press.
The Sound of Fractions
205
Empson, S. B. (1999). Equal sharing and shared meaning: The development of fraction concepts
in a first-grade classroom. Cognition and Instruction, 17(3), 283–342.
Empson, S. B., & Levi, L. (2011). Extending Children’s Mathematics: Fractions and
Decimals:[innovations in Cognitively Guided Instruction]. Heinemann Portsmouth, NH.
Eves, H. (1969). An introduction to the history of mathematics . New York: Holt, Rinehart and
Winston. Inc.
Fey, J. T. (1989). Technology and mathematics education: A survey of recent developments and
important problems. Educational Studies in Mathematics, 20(3), 237–272.
Gamoran, A. (2007). Standards-based reform and the poverty gap: Lessons for No Child Left
Behind. Brookings Institution Press.
Gill, S. P. (2012). Rhythmic synchrony and mediated interaction: towards a framework of
rhythm in embodied interaction. AI & Society, 27(1), 111–127.
Grainger, C. (n.d.). Coding is not the new literacy. Retrieved from http://www.chris-
granger.com/2015/01/26/coding-is-not-the-new-literacy/
Graziano, A. B., Peterson, M., & Shaw, G. L. (1999). Enhanced learning of proportional math
through music training and spatial-temporal training. Neurological Research, 21(2), 139–
152.
Gromko, J. E. (1994). Children’s invented notations as measures of musical understanding.
Psychology of Music, 22(2), 136–147.
Hetland, L. (2000). Learning to make music enhances spatial reasoning. Journal of Aesthetic
Education, 179–238.
Holland, S., Bouwer, A. J., Dalgelish, M., & Hurtig, T. M. (2010). Feeling the beat where it counts:
fostering multi-limb rhythm skills with the haptic drum kit. In Proceedings of the fourth
international conference on Tangible, embedded, and embodied interaction (pp. 21–28).
Howison, M., Trninic, D., Reinholz, D., & Abrahamson, D. (2011). The Mathematical Imagery
Trainer: from embodied interaction to conceptual learning. In Proceedings of the SIGCHI
Conference on Human Factors in Computing Systems (pp. 1989–1998).
Initiative, C. C. S. S., & others. (2012). Common core state standards for English language arts &
literacy in history/social studies, science, and technical subjects. Common Core Standards
Initiative.
Jordà, S., Geiger, G., Alonso, M., & Kaltenbrunner, M. (2007). The reacTable: exploring the
synergy between live music performance and tabletop tangible interfaces. In Proceedings
of the 1st international conference on Tangible and embedded interaction (pp. 139–146).
Jordan, A., Lindsay, L., & Stanovich, P. J. (1997). Classroom teachers’ instructional interactions
The Sound of Fractions
206
with students who are exceptional, at risk, and typically achieving. Remedial and Special
Education, 18(2), 82–93.
Kaput, J. J., & Thompson, P. W. (1994). Technology in mathematics education research: The first
25 years in the JRME. Journal for Research in Mathematics Education, 25(6), 676–684.
Kieren, T. E. (1976). On the Mathematical, Cognitive and Instructional. In Number and
Measurement. Papers from a Research Workshop. (Vol. 7418491, p. 101).
Kirschner, S., & Tomasello, M. (2009). Joint drumming: social context facilitates synchronization
in preschool children. Journal of Experimental Child Psychology, 102(3), 299–314.
Lamon, S. J. (2007). Rational numbers and proportional reasoning: Toward a theoretical
framework for research. Second Handbook of Research on Mathematics Teaching and
Learning, 1, 629–667.
Landers, R. (1984). The Talent Education School of Shinichi Suzuki: An Analysis: Application of
Its Philosophy and Methods to All Areas of Instruction.
Lee, J. S., & Tatar, D. (2014). Sounds of silence: exploring contributions to conversations, non-
responses and the impact of mediating technologies in triple space. In Proceedings of the
17th ACM conference on Computer supported cooperative work & social computing (pp.
1561–1572).
Lester, F. K. (2007). Second handbook of research on mathematics teaching and learning: A
project of the National Council of Teachers of Mathematics (Vol. 1). IAP.
McFerrin, B. (n.d.). Bobby McFerrin Demonstrates the Power of the Pentatonic Scale.
McPherson, G. E., & Gabrielsson, A. (2002). From sound to sign. The Science and Psychology of
Music Performance: Creative Strategies for Teaching and Learning, 99–116.
Neal, J. (2000). Songwriter’s Signature, Artist's Imprint. Country Music Annual 2000, 112.
Neufeld, K. A. (1986). Understanding of selected pre-number concepts: Relationships to a
formal music program. Alberta Journal of Educational Research.
Newman, D., Griffin, P., & Cole, M. (1989). The construction zone: Working for cognitive change
in school. Cambridge University Press.
No Title. (n.d.-a). Retrieved from http://quickfacts.census.gov/qfd/states/51
No Title. (n.d.-b). Retrieved from Intentionally
Norton, A., & Wilkins, J. L. M. (2009). A quantitative analysis of children’s splitting operations
and fraction schemes. The Journal of Mathematical Behavior, 28(2), 150–161.
Norton, A., & Wilkins, J. L. M. (2013). Supporting Students’ Constructions of the Splitting
Operation. Cognition and Instruction, 31(1), 2–28.
The Sound of Fractions
207
Panel, N. M. A. (2008). Foundations for success: The final report of the National Mathematics
Advisory Panel. US Department of Education.
Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas. Basic Books, Inc.
Patten, J., Recht, B., & Ishii, H. (2002). Audiopad: a tag-based interface for musical performance.
In Proceedings of the 2002 conference on New interfaces for musical expression (pp. 1–6).
Pothier, Y., & Sawada, D. (1983). Partitioning: The emergence of rational number ideas in young
children. Journal for Research in Mathematics Education, 307–317.
Radha, M. (2012). Mediated interactions in musical expression.
Rands, S. A., Cowlishaw, G., Pettifor, R. A., Rowcliffe, J. M., & Johnstone, R. A. (2003).
Spontaneous emergence of leaders and followers in foraging pairs. Nature, 423(6938),
432–434.
Reimer, B. (1999). Facing the Risks of the“ Mozart Effect.” Grand Masters Series. Music
Educators Journal, 86(1), 37–43.
Salsberg, P. (2014, February). No Title. Retrieved from
https://www.youtube.com/watch?v=g0aM3qxR3E8
Segal, A. (2011). Do gestural interfaces promote thinking? Embodied interaction: Congruent
gestures and direct touch promote performance in math. Columbia University.
Selecta, C. (n.d.). Synchronized clapping: a two-way synchronized process.
Shaffer, D. W., & Kaput, J. J. (1998). Mathematics and virtual culture: An evolutionary
perspective on technology and mathematics education. Educational Studies in
Mathematics, 37(2), 97–119.
Sinor, J. (1997). The Ideas of Kod{á}ly in America This article on the application of Zolt{á}n
Kod{á}ly’s teaching method in the United States was first published in the Music Educators
Journal in February 1986. Music Educators Journal, 83(5), 37–41.
Steffe, L. P. (2002). A new hypothesis concerning children’s fractional knowledge. The Journal of
Mathematical Behavior, 20(3), 267–307.
Swift, T. (2014). Shake It Off.
Tatar, D., Lee, J.-S., & Alaloula, N. (2008). Playground games: a design strategy for supporting
and understanding coordinated activity. In Proceedings of the 7th ACM conference on
Designing interactive systems (pp. 68–77).
Trehub, S. E., & Hannon, E. E. (2006). Infant music perception: Domain-general or domain-
specific mechanisms? Cognition, 100(1), 73–99.
Upitis, R. (1993). Children’s invented symbol systems: Exploring parallels between music and
The Sound of Fractions
208
mathematics. Psychomusicology: A Journal of Research in Music Cognition, 12(1), 52.
Vaughn, K. (2000). Music and mathematics: Modest support for the oft-claimed relationship.
Journal of Aesthetic Education, 149–166.
Weeden, R. E. (1972). A comparison of the academic achievement in reading and mathematics
of Negro children whose parents are interested, not interested, or involved in a program of
Suzuki violin. ProQuest Information & Learning.
Wilkins, J. L. M., & Norton, A. (2011). The Splitting Loope. Journal for Research in Mathematics
Education, 42(4), 386–416.
Wing, J. M. (2006). Computational Thinking. COMMUNICATIONS OF THE ACM, Vol. 49(3), 33–
35.
Wing, J. M. (2008). Computational thinking and thinking about computing. Philos Trans A Math
Phys Eng Sci, 366(1881), 3717–3725. doi:10.1098/rsta.2008.0118
Winner, E. (2007). Development in the arts: Drawing and music. Handbook of Child Psychology.

